Quarter Circle – Introduction
In our everyday lives, we come across many shapes in the form of various objects, like a square table, a rectangular tray, a football in the shape of a circle, oval eggs, etc.
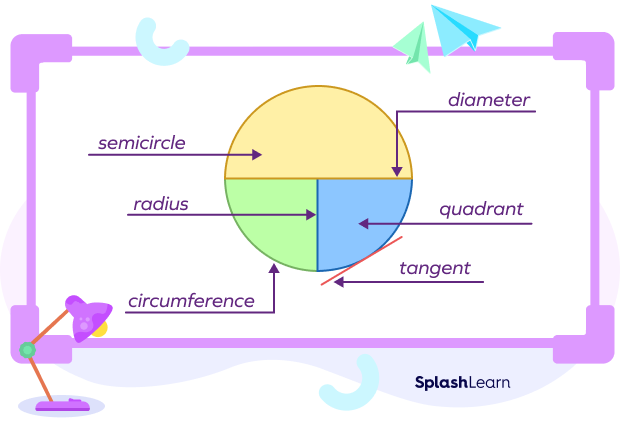
Have you ever observed the shape of a slice of pizza when divided into 4 equal parts? It looks like a triangle, but one of the sides is actually curvy. This shape is called a quarter circle.

Recommended Games
What Is a Quarter Circle?

A quarter of anything means one-fourth of that object or thing. Thus, by a quarter of a circle, we mean one-fourth of the circle. We can also get a quarter circle by dividing a semicircle into two halves.
The following image shows division of a circle in quarters.
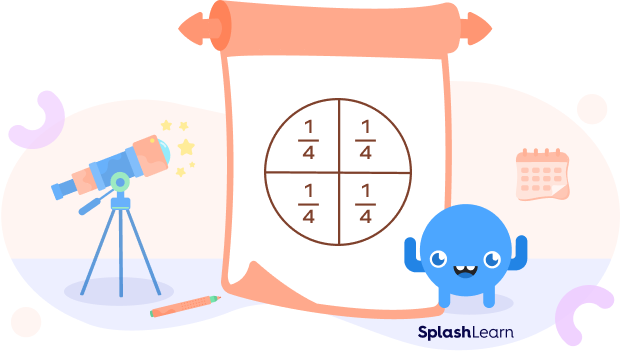
In mathematical terms, the area created by two perpendicular radii and one-fourth area of the circumference of a whole circle is called a quarter circle. It is also often referred to as a quadrant.
Recommended Worksheets
Area of a Quarter Circle
One-fourth area of a whole circle is known as the area of a quadrant or a quarter of a circle.
Quarter circle formula for area can be given as:
Area of a quarter circle $=$ Area of circle $/ 4 = \frac{π\text{r}^2}{4}$
Note:
The value of $π = 22/7$ or, $3.14$
Perimeter of a Quarter Circle
The perimeter of a quarter circle consists of two radii and the circumference of a quarter circle (which is the one fourth part of the circumference of a circle). Hence, the formula for calculating it would be as follows:
Perimeter of a Quarter Circle $= \text{r} + \text{r} + (\frac{2π\text{r}}{4}) = 2\text{r} + (\frac{π\text{r}}{2})$
Solved Examples
Example 1: If the radius of a circle is 6 cm, what will be the area of a quarter of its circle?
Solution:
Area of a quadrant $= π\frac{\text{r}^2}{4}$
$= \frac{3.14 \times 6 \times 6}{4}$
$= \frac{113.04} {4}$
$= 28.26 \text{cm²}$
Example 2: If the diameter of a circle is 32 cm, what will be the area of a quarter circle?
Solution:
Diameter of the circle $= 32$ cm
So, radius of the circle $= \text{diameter}/2 = 32/2 = 16 \text{cm}$
Area of quadrant $= \frac{π\text{r}}{24} = \frac{3.14 \times 16 \times 16} {4} = 200.96 \text{cm²}$
Example 3: A circular park has a radius of 35 yards. One-quarter of the park has a playground for toddlers. Find the perimeter of the playground.
Solution:
The total radius of the park $(\text{r}) = 35$ yards
The perimeter of the quarter of the park $= 2\text{r} +$ $(\frac{π\text{r}}{2})$
$= 2 \times 35 + ( \frac{3.14 \times 35} {2})$
$= 70 + 54.95$
$= 124.95$ yards
Practice Problems
Quarter Circle
Choose the correct formula for calculating the area of a quarter circle.

The formula to calculate the area of a quarter of a circle is $\frac{\text{πr}^2}{4}$
Sam ordered a 16-inch pizza for himself and his 3 friends. They want to share the pizza equally among themselves. Find the quantity of pizza each one got. $(\text{Use} π = 3.14)$
Radius of the pizza $(\text{r}) = d / 2$
$= 16 / 2 = 8$ inches
Area of each quarter portion of pizza $= \frac{\text{πr}^2}{4} = \frac{3.14 \times 8 \times 8}{4}$
$= 50.24$ square inches
What is the perimeter of a quarter circle whose radius is 14 units?
Given radius of the circle $= 14$ units
The perimeter of a quarter circle $= 2r + (\frac{\text{πr}}{2})$
$= 2 \times 14 + (\frac{3.14 \times 14}{2}$)
$= 28 + 21.98$
$= 49.98$ units
Frequently Asked Questions
What is another term used for a quarter circle?
A quarter-circle is also known as a quadrant and is formed by dividing a whole circle into four equal parts.
Is the radius of a quarter circle different from the radius of the whole circle?
No, the radius of a quadrant will always be equal to the radius of the whole circle.
How can we calculate the area of a quarter circle by using the radius?
If the circle has a radius r, then area of the quadrant $= π\text{r}² / 4$