Number Line – Definition, Types, Examples, Facts, FAQs

What Is a Number Line in Math?

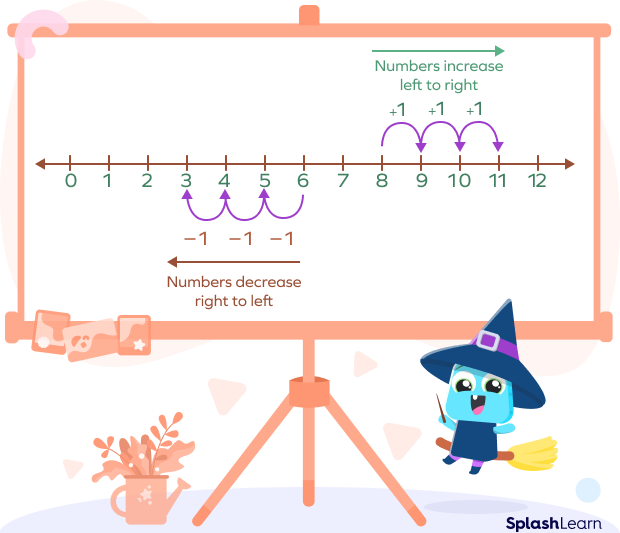
In math, a number line can be defined as a pictorial representation of numbers on a straight line. The numbers on a number line are placed sequentially at equal distances along its length. It can be extended infinitely in any direction and is usually represented horizontally. 

The numbers on a number line increase as one moves from left to right and decrease on moving from right to left. 

Different Types of Numbers on a Number Line

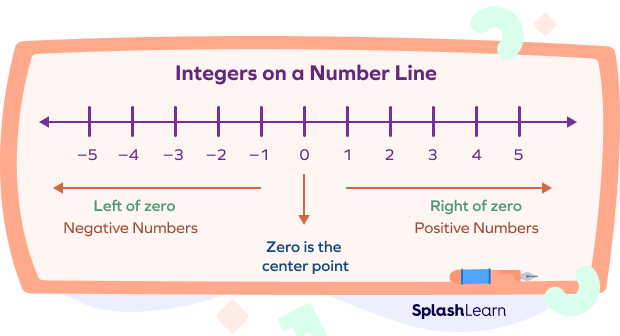
A number line can be used to represent any type of numbers, like fractions, decimals, integers, etc.

Number Lines as Mathematical Tools

• To compare numbers

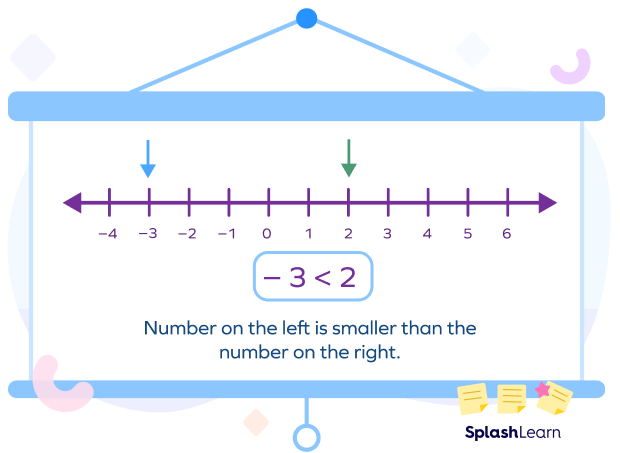
Writing numbers on it makes comparing numbers easier. Numbers on the left are smaller than the numbers on the right of it.

• To add/subtract numbers

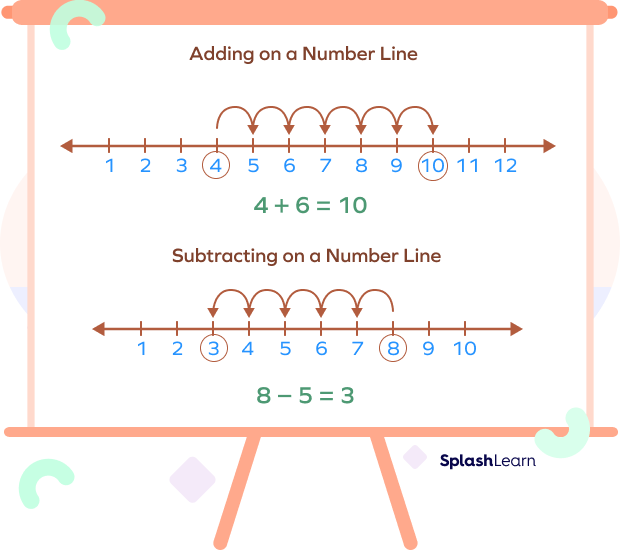
A number line can also be used to carry out addition and subtraction. We move right to add, move left to subtract. Let’s have a look. 

Steps to add/subtract on a number line:

1. Locate the first number on the number line. 
2. To add: move as many steps as the second number to the right.
   To subtract: move as many steps as the second number to the right.
3. The number you land on is the answer. 

• To multiply/divide numbers

A number line can also be used to carry out multiplication and division. We skip count on a it to show jumps of equal size. Let’s have a look.

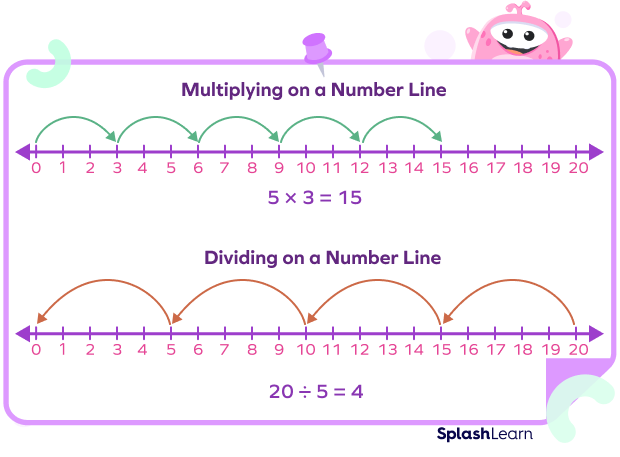
Fun Facts

1. A number line is usually represented horizontally and can be extended infinitely in any direction.
2. The first mention of the number line as a tool for adding and subtracting is found in the Treatise on Algebra by John Wallis. In his work, Wallis describes addition and subtraction on it in terms of moving forward and backward, in the context of a person walking.
3. A blank number line is a visual diagram with no numbers or markers and is essentially used as a tool for solving word problems.

Let us practice number line examples to understand it even better.

Solved Examples on Number Line

Example 1: Compare $–25$ and $15$ using a number line.

Solution: Let’s locate –25 and 15 on the number line. 

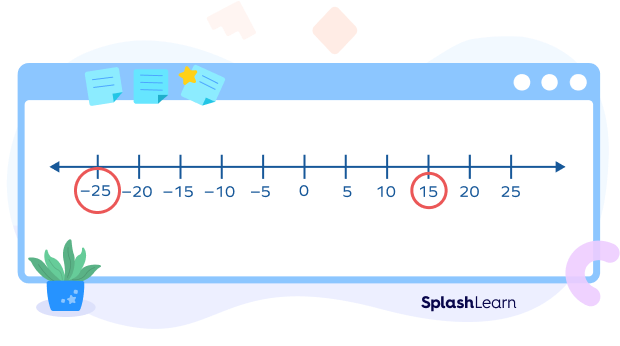
Since, $–25$ is to the left of $15$,  $–25 \lt 15$. 

Example 2: Add $–7 + 7$.

Solution: Let’s locate –7 on the number line and move 7 steps to the right to find the answer. 

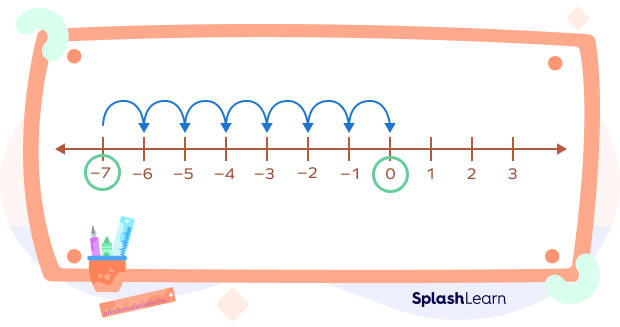
So, $–7 + 7 = 0$

Example 3: Subtract $6 $–$ 7$.

Solution: Let’s locate 8 on the number line and move 11 steps to the left to find the answer. 

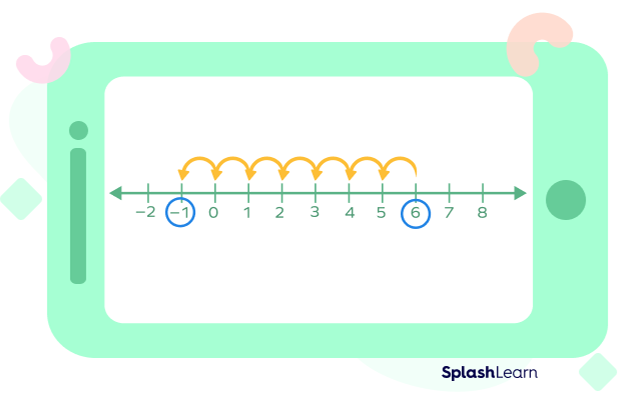
So, $6 $–$ 7 = –1$.

Example 4. Multiply $2 \times 8$.

Solution: Starting from 0, let’s make 2 jumps of 8 to the right on the number line to find the answer. 

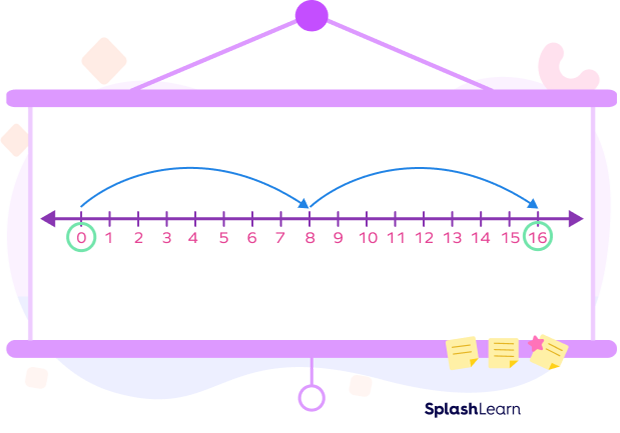
So, $2 \times 8 = 16$.

Conclusion

One can mark positive, negative, whole numbers, and rational numbers with a number line. Numbers appearing on the right side of 0 are positive numbers, and those reflected on the left side of it are negative. Using it, one can compare numbers and carry out arithmetic operations such as: addition, subtraction, multiplication, and division.

Practice Problems on Number Line

Frequently Asked Questions on Number Line