What Are Prime Numbers?
Prime numbers are numbers greater than 1 that only have two factors, 1 and the number itself. This means that a prime number is only divisible by 1 and itself. If you divide a prime number by a number other than 1 and itself, you will get a non-zero remainder.
Numbers that have more than 2 factors (but finite number of factors) are known as composite numbers.
Recommended Games
Prime Numbers Definition
A prime number can be defined as a natural number greater than 1 whose only factors are 1 and the number itself.
A prime number is a positive integer greater than 1 that cannot be written as a product of two distinct integers which are greater than 1.
Recommended Worksheets
Examples and Non-examples of Prime Numbers
 | 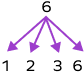 |  |
| 7 is a prime number. 7 has only two factors, 1 and 7. | 6 is NOT a prime number. 6 has four factors (1, 2, 3, and 6). 6 is a composite number. | 1 is neither prime nor composite. 1 has only one factor, which is 1 itself. |
Properties of Prime Numbers
- Prime numbers are natural numbers greater than 1.
- 2 is the smallest prime number.
- 2 is the only even prime number. All the prime numbers except 2 are odd.
- Any two prime numbers are always coprime.
- Any composite number can be uniquely expressed as the product of its prime factors.
- A prime number has only two factors $— 1$ and the number itself.
- If two prime numbers have only 1 composite number between them, they are called twin-prime numbers.
- Every even positive integer greater than 2 can be written as the sum of two prime numbers.
- Every positive integer greater than 1 has at least one prime factor.
Difference Between Prime Number and Composite Number
| Prime Number | Composite Number |
|---|---|
| A prime number is a natural number greater than 1 that has only two factors – 1 and the number itself. | A composite number is a natural number or a positive integer that has more than 2 factors. |
| A prime number is divisible only by 1 and the number itself. For example, 3 is divisible only by 1 and 3. | A composite number is divisible by all its factors. For example, 12 is divisible by 1, 2, 3, 4, 6, and 12. |
| 2 is the smallest prime number. | 4 is the smallest composite number. |
| A prime number cannot be written as the product of two distinct positive integers. | A composite number can be written as the product of two smaller positive integers. |
| Examples: 2, 3, 5, 7, etc. | Examples: 4, 6, 8, 9, etc. |
The Sieve of Eratosthenes
In the third century B.C. the Greek mathematician, Eratosthenes, found a very simple method of finding the prime numbers.
Follow the given steps to identify the prime numbers between 1 and 100.
Step 1: Make a hundreds chart. (Write all the natural numbers between 1 to 100 using 10 rows and 10 columns.)
Step 2: Leave 1 as it is neither a prime number nor composite number.
Step 3: Encircle 2 and cross out all its multiples (such as 4, 6, 8, 10, and so on) as they are not prime.
Step 4: Encircle the next uncrossed number which is 3 and cross out all its multiples. Ignore the previously crossed out numbers like 6, 12 and 18 and so on.
Step 5: Continue the process of encircling the next uncrossed number and crossing out its multiples till all the numbers in the table are either encircled or crossed except 1.

So, from the table it is clear that 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 are the prime numbers.
There are 25 prime numbers between 1 and 100.
How to Find Prime Numbers
1) Every prime number (except 2 and 3) can be written in the form of 6n + 1 or 6n – 1.
To check whether a given number is prime or not, you can simply check if it can be written in the form $6n + 1$ or $6n \;-\; 1$.
Examples: 13 can be expressed as $6(2) + 1$. Thus, 13 is a prime number.
$6(1) \;–\; 1 = 5$
$6(1) + 1 = 7$
$6(2)\; –\; 1 = 11$
$6(2) + 1 = 13$
$6(3) \;–\; 1 = 17$
$6(3) + 1 = 19$
(Note that we do not consider the multiples of prime numbers when we use this method. For example, 25 and 49 can be written as $25 = 6(4) + 1,\; 49 = 6(8) \;-\; 1$, but they are not prime numbers.)
2) To find the prime numbers greater than 40, we can use this method.
If we can express a number greater than 40 in the form $n^{2} + n + 41$, where $n = 0,\; 1,\; 2,\; …..,\; 39$, then it is a prime number.
Examples:
$(0)^{2} + 0 + 0 = 41$
$(1)^{2} + 1 + 41 = 43$
$(3)^{2} + 3 + 41 = 53$
3) You can use the factorization method and find the number of factors the number has. If it has 2 unique factors – 1 and itself, it is a prime number. Otherwise, it is composite.
For example, to find the factors of n, divide n by each natural number up to n. If the remainder is 0, it is a factor.
| Prime number | Not a prime number |
|---|---|
| $13 \div 1 = 13$ and Remainder $= 0$ $13 \div 13 = 1$ and Remainder $= 0$ | $4 \div 1 = 1$ and Remainder $= 0$ ..factor $4 \div 2 = 2$ and Remainder $= 0$ ..factor $4 \div 3 = 1$ and Remainder $= 1$ $4 \div 4 = 1$ and Remainder $= 0$ ..factor Thus, 4 has 3 factors (1, 2, and 4). It is not a prime number. |
Co-Prime Numbers and Twin Prime Numbers
Co-Primes: Two numbers are said to be co-primes if they have only 1 common factor, that is, 1. It is not necessary for these numbers to be prime numbers. For example, 9 and 10 are co-primes. Let’s verify.
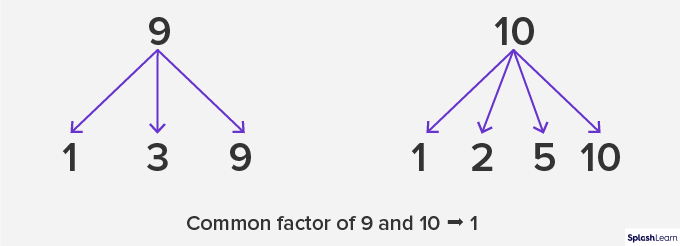
Note that any two prime numbers are always co-prime. This is because out of their two factors, the common factor can only be 1. So, (3, 5), (11, 19) are some examples of co-primes.
Twin-Primes: A pair of prime numbers are known as twin primes if there is only one composite number between them. For example, (3, 5), (5, 7), (11, 13), (17, 19), etc.
Prime Numbers List
Take a look at the ‘prime numbers charts’ and check out the organized lists of prime numbers in the given range.
List of Prime Numbers between 1 and 100
There are 25 prime numbers between 1 and 100.
Prime numbers between 1 to 100 are as follows:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
| Prime Numbers 1-100 | |
|---|---|
| Prime numbers between 1 and 10 | 2, 3, 5, 7 |
| Prime numbers between 10 and 20 | 11, 13, 17, 19 |
| Prime numbers between 20 and 30 | 23, 29 |
| Prime numbers between 30 and 40 | 31, 37 |
| Prime numbers between 40 and 50 | 41, 43, 47 |
| Prime numbers between 50 and 60 | 53, 59 |
| Prime numbers between 60 and 70 | 61, 67 |
| Prime numbers between 70 and 80 | 71, 73, 79 |
| Prime numbers between 80 and 90 | 83, 89 |
| Prime numbers between 90 and 100 | 97 |
List of Prime Numbers between 1 and 200
There are 46 prime numbers between 1 and 200.
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 |
List of Prime Numbers between 1 and 1000
| Prime Numbers Between | List of Prime Numbers | Total |
|---|---|---|
| 1 to 100 | 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 | 25 |
| 101-200 | 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199 | 21 |
| 201-300 | 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293 | 16 |
| 301-400 | 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397 | 16 |
| 401-500 | 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499 | 17 |
| 501-600 | 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599 | 14 |
| 601-700 | 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691 | 16 |
| 701-800 | 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797 | 14 |
| 801-900 | 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887 | 15 |
| 901-1000 | 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997 | 14 |
| Total number of prime numbers between 1 to $1000 = 168$ | ||
Facts about Prime Numbers
- 2 is the smallest prime number.
- 2 is the only prime number which is even.
- 2 and 3 are the only consecutive prime numbers.
- Except for 0 and 1, a whole number is either a prime number or a composite number.
- No prime number greater than 5 ends in a 5.
- Sieve of Eratosthenes is one of the earliest methods of finding prime numbers.
- Prime numbers get more rare as the number gets bigger.
- There is no largest prime number. The largest known prime number (as of September 2021) is $2^{82,589,933} \;−\; 1$, a number which has 24,862,048 digits when written in base 10. By the time you read this it may be even larger.
Conclusion
In this article, we learned about prime numbers, their properties, methods to find prime numbers, and different lists of prime numbers. Let’s solve a few examples and practice problems based on these concepts for better understanding.
Solved Examples on Prime Numbers
Example 1: Classify the given numbers as prime numbers or composite numbers.
13, 48, 49, 23, 74, 80, 71, 59, 45, 47
Solution:
| Prime Numbers | Composite Numbers |
|---|---|
| 13, 23, 71, 59, 47 | 48, 49, 74, 80, 45 |
Example 2: Express 21 as the sum of two prime numbers.
Solution:
We can write 21 as
$21 = 19 + 2$
Here, 2 and 19 are both prime numbers.
Example 3: What prime numbers are there between 20 and 30?
Solution:
The prime numbers between 20 and 30 are 23 and 29.
Example 4: What is the greatest prime number between 80 and 90?
Solution:
The prime numbers between 80 and 90 are 83 and 89.
So, 89 is the greatest prime number between 80 and 90.
Practice Problems on Prime Numbers
Prime Numbers
Which of the following is not a prime number?
The factors of 81 are 1, 3, 9, 27, and 81. Rest of the numbers have only 2 factors— 1 and the number itself.
What is the 10th prime number?
2, 3, 5, 7, 11, 13, 17, 19 and 23 are the first 9 prime numbers and 29 is the 10th prime number.
How many prime numbers are there between 40 and 50?
Prime numbers between 40 and 50 are 41, 43 and 47.
Which is the smallest odd prime number?
2 is the smallest even prime number. Next prime number is 3, so 3 is the smallest odd prime number.
Which of the following pairs of numbers are co-prime?
Co-prime numbers have only 1 as their common factor.
Common factors of 7 and 14 are 1 and 7;
Common factors of 15 and 27 are 1 and 3;
Common factors of 25 and 35 are 1 and 5;
Common factor of 8 and 55 is 1.
Frequently Asked Questions on Prime Numbers
Is 1 a prime number?
No, 1 is neither a prime number nor a composite number.
Can a prime number be negative?
No, prime numbers cannot be negative. Prime numbers are natural numbers greater than 1.
Why is 2 the only even prime number?
All even numbers larger than 2 are multiple of 2. So, 2 is the only even prime number.
What is the difference between prime numbers and co-prime numbers?
A prime number is a natural number greater than 1 that has only two factors – 1 and the number itself. A pair of numbers whose HCF is 1 (the only common factor is 1) are called co-prime numbers.
Which is the largest known prime number?
The largest known prime number (as of September 2021) is 282,589,933 − 1, a number which has 24,862,048 digits. By the time you read this it may be even larger than this.
What is the lowest prime number?
The smallest prime number is 2.
What makes a number prime?
If a number has only two factors (1 and itself), it is a prime number. If it has more than two factors, it is composite.
How to check if a number is prime?
Find the factors of the given number. Check the number of factors. If there are more than 2 factors, the number is not prime. If there are only two factors (1 and number itself), the number is prime.
What are the first ten prime numbers?
The first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Why 0 and 1 are neither prime nor composite?
Any number multiplied by 0 results in 0. So, 0 has infinitely many factors. However, a composite number can have only a finite number of factors. Also, $0 \lt 1$ and prime numbers are natural numbers greater than 1.
1 has only 1 factor, itself. So, 0 and 1 do not fit into the definitions of prime & composite numbers.
What is the total number of prime numbers up to 100?
There are 25 prime numbers between 1 and 100.




































