Three Dimensional Shapes (3D Shapes)- Definition, Examples

What Are Three Dimensional Shapes?

In geometry, a three dimensional shape can be defined as a solid figure or an object or shape that has three dimensions— length, width, and height. Unlike two dimensional shapes, three-dimensional shapes have height, which is the same as thickness or depth. Three dimensional is also written as 3D and hence, these figures are commonly called 3D shapes too. All three dimensional figures occupy space, which is measured in terms of volume.

In 3D shapes, 3D refers to three-dimensionality. Dimensions can usually be thought of as measurements in a direction. Length, width, and depth can be considered dimensions.

History of 3D Shapes

All 3D shapes have three measurements: length, width, and height. Shapes look different from different directions. All 2D shapes are only measured by their length and width. Aristotle said that 2D shapes are lines and not figures or bodies. They are always described as extensions of lines or areas bounded by lines. Conversely, 3D shapes have volume.

By convention, the first three dimensions are represented as spatial dimensions x-y-z. Width, height, and depth are their respective names. 

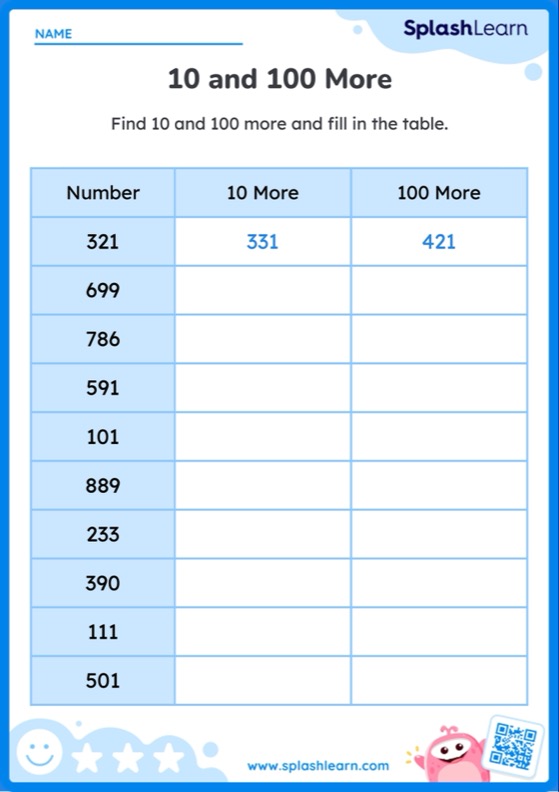
Examples of Three Dimensional Shapes

A cube, rectangular prism, sphere, cone, and cylinder are the basic three dimensional figures we see around us. 

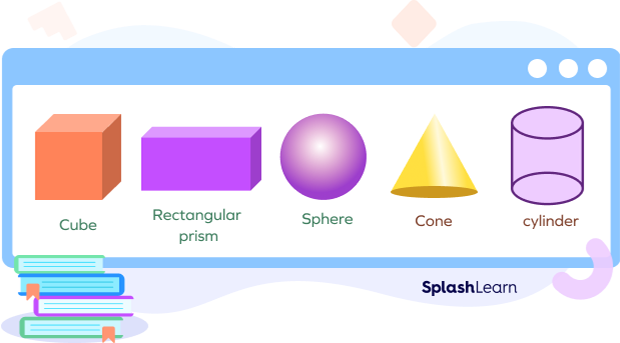
Real-life Examples of Three Dimensional Shapes

3D shapes can be seen all around us. We can see a cube in a Rubik’s Cube and a die, a rectangular prism in a book and a box, a sphere in a globe and a ball, a cone in a carrot and an ice cream cone, and a cylinder in a bucket and a barrel around us. 

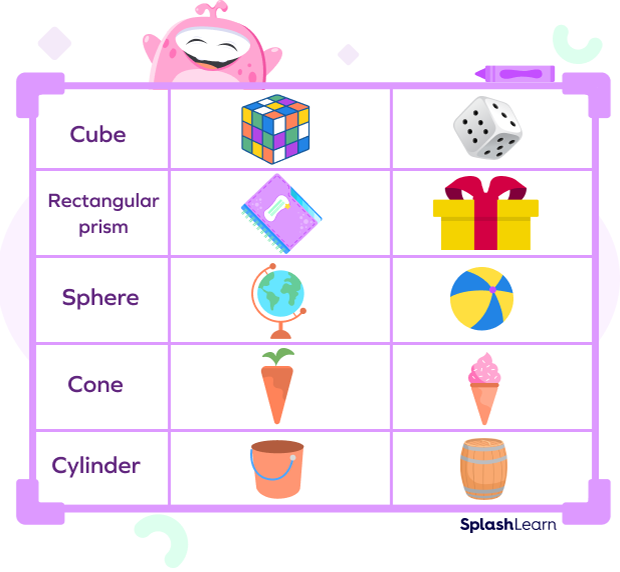
Some real-life examples of 3D shapes are listed below:

1. Cone: Traffic cones and birthday caps are cone-shaped.

2. Triangular prism: A tent is the shape of a triangular prism.

3. Square pyramid: The pyramid of Giza in Egypt is the shape of a square pyramid.

4. Rectangular prism: Boxes such as shoe boxes and cereal boxes are shaped like rectangular prisms. 

Attributes of Three Dimensional Shapes

There are three attributes of a three dimensional figure: face, edge, and vertex. Let’s understand three dimensional shapes and their properties in detail.

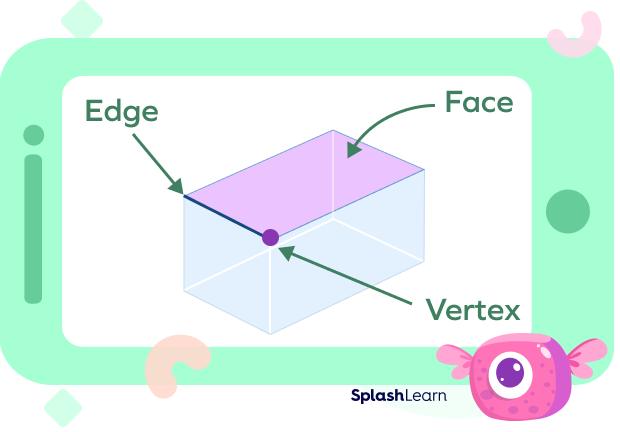
Face: Each single surface, flat or curved, of the 3D figure is called its face.

Edge: The line, where two faces of the 3D figures meet, is called its edge.

Vertex: Each corner, where three faces of 3D figures meet, is called its vertex. Vertices are the plural of the vertex.

List of Three Dimensional Shapes

Here’s a list of the names of three dimensional shapes with their pictures, and attributes.

Sphere

All the points on a sphere are at the same distance from its center. The Earth is like that in some ways, except for one: when you look at it from far away, it looks like a sphere, but when you look at it from up close, it is not truly round. A sphere has several characteristics:

• It is perfectly symmetrical and shaped just like a ball.
• It also has length besides radius, diameter, circumference, volume, and area.
• The distance from the center to every point on the surface of a sphere is equal.
• No edges or vertices are found on its one face.
• Since it does not have a flat face, it is not a polyhedron.

Cube and Cuboid

A cube and a cuboid are both big blocks. The difference between them is that a cube has square faces, while a cuboid has rectangular faces.

Cylinder

A cylinder has two circular faces on both its ends and one curved surface along its length. It has height and radius. A cylinder’s height is perpendicular to its surface, from top to bottom. The following are some fundamental characteristics of cylinders:

• The face of a cylinder is curved.
• From the bottom to the top, its shape remains the same.
• Two identical ends shape the object’s three-dimensional form. The ends can be round or oval.
• A right cylinder has the centers of its circular bases along the same line, while an oblique cylinder has the centers of its bases along different lines.

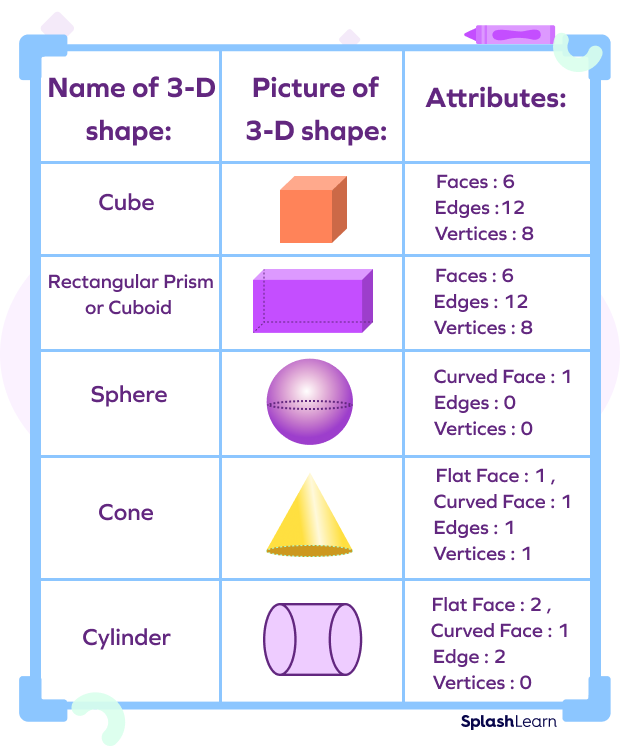
Formula of Three Dimensional Shapes

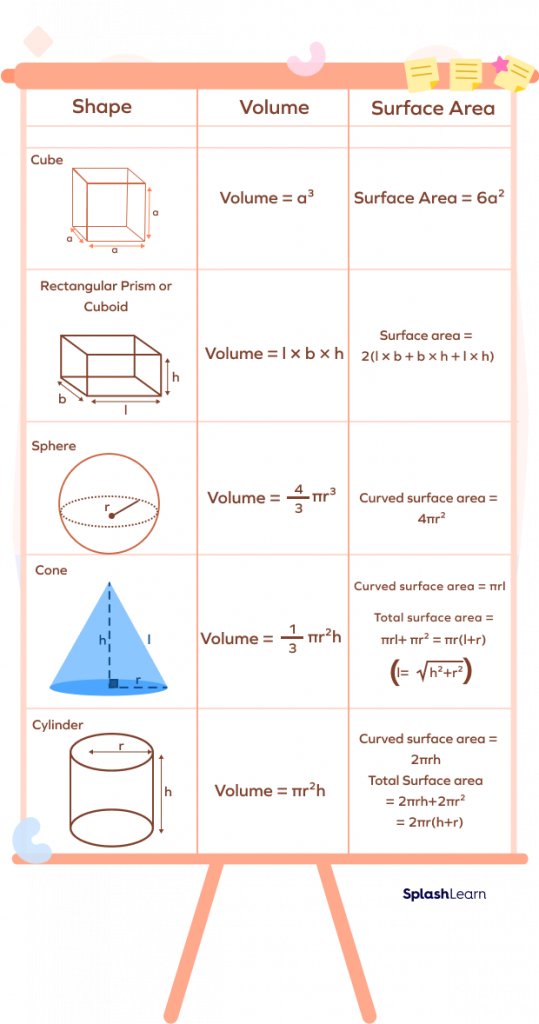
Net of Three Dimensional Shapes

A net is a pattern made when the surface of a 3D figure is laid out flat, showing each face of the figure.

3D figures can have more than one net pattern. A few 3D shapes names and their nets are shown below:

Fun Facts:
All three dimensional shapes are made up of two dimensional shapes.

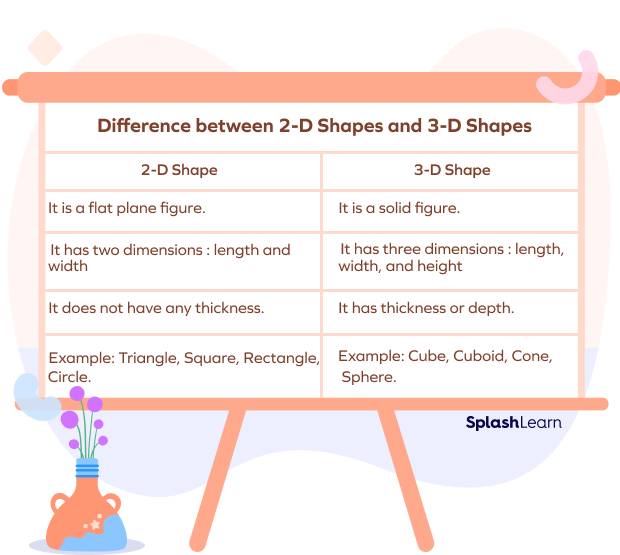
Difference between 2D Shapes and 3D Shapes

Let’s differentiate between 2D and 3D shapes by understanding two dimensional and three dimensional shapes and their properties.

Solved Examples of Three Dimensional Shapes

Example 1: Which of the following is a 3D shape?

Cone Square Sphere Cuboid Cylinder Parallelogram

Solution:

Cone Sphere Cuboid Cylinder

Example 2: State whether the following are true or false.

1. A three-dimensional shape has 3 dimensions.
2. Three-dimensional shapes are also called flat shapes.
3. Three-dimensional shapes occupy space.
4. All three-dimensional shapes have flat faces.

Solution:

1. True
2. False. Three-dimensional shapes are also called solid shapes.
3. True
4. False. Sphere is a three-dimensional shape with no flat face.

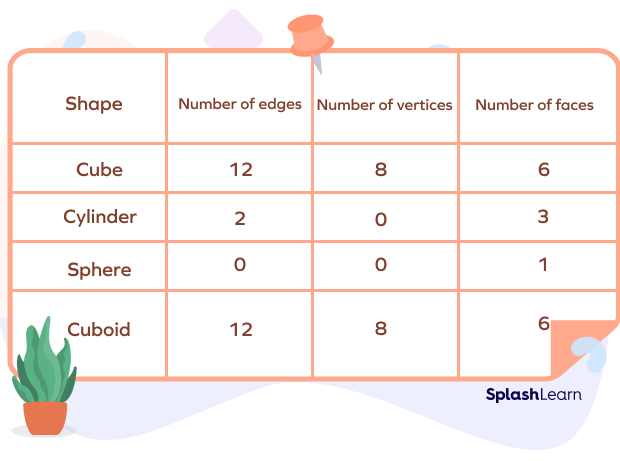
Example 3: Complete the table with attributes of the 3D shapes listed.

Solution:

Example 4: Match the object with its shape.

Solution:

1. (a) – (iii)
2. (b) – (i)
3. (c) – (iv)
4. (d) – (ii)

Example 5: Calculate the surface area of a cuboid with a width of 4 units, length of 3 units, and height of 5 units. 

Solution:

Given, the cuboid has three units of length, four units of width, and five units of height.

Surface area of the cuboid $= 2 \times (\text{lw} + \text{wh} + \text{lh})$ square units

$= 2 \times (\text{lw} + \text{wh} + \text{lh})$

$= 2[(3 \times 4) + (4 \times 5) + (3 \times 5)]$

$= 2(12 + 20 + 15)$

$= 2(47)$

$= 94$ square units

Therefore, the surface area of the given cuboid is 94 square units.

Example 6: Jane likes to drink milk from a cylinder-shaped glass. Her glass has 15 units of height and 3 units of base radius. How much milk can she fill in the glass?

Solution:

Given that the height of the glass is 15 units, and the radius of the base is 3 units.

Using the formula for the volume of a cylinder, we can find the volume of the glass.

The volume of the glass, $\text{V} = \pi $$r^2 \text{h}$

$= \pi(3)​^2​​​​​(15)$

$= 135\pi$  

$= 424.11 \text{in}^2$

Therefore, Jane can fill approximately 424 cubic units of milk in her glass.

Practice Problems of Three Dimensional Shapes

Frequently Asked Questions of Three Dimensional Shapes