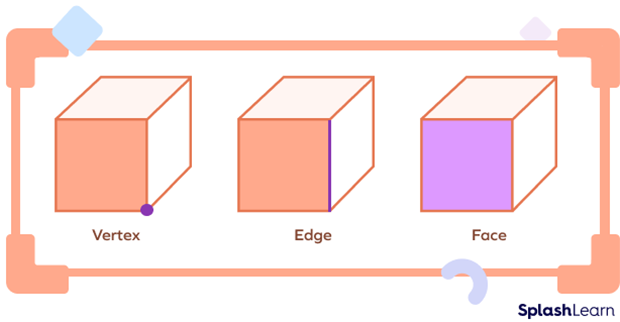
What Are Vertices, Faces, Edges?
Every geometric shape is composed of different parts such as vertices, faces, edges. We come across different objects with rectangular faces, circular faces, cubic faces, diamond faces, triangular faces, etc. We also know many objects that have sharp corners and edges. We will learn about vertices, faces, edges of different plane shapes and geometric shapes. First, let’s understand plane shapes and solid shapes.
Recommended Games
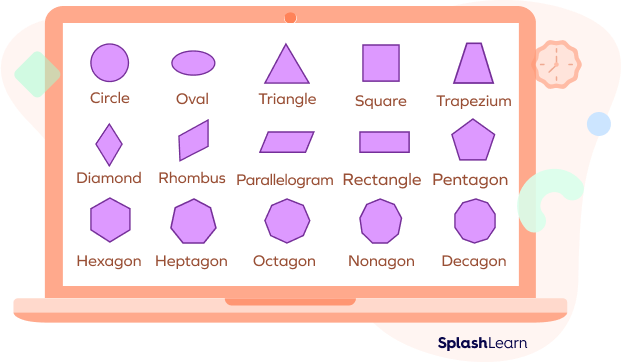
Plane Shapes
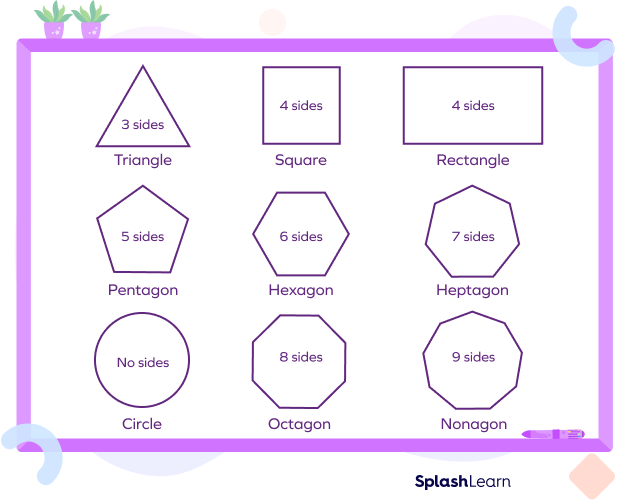
Any two-dimensional shape that is closed and flat is known as a plane shape. Plane shapes do not have thickness. Different plane shapes have different characteristics, like the number of vertices, the number of sides, etc.
Some examples of plane shapes are circles, triangles, rectangles, ovals, polygons, etc.
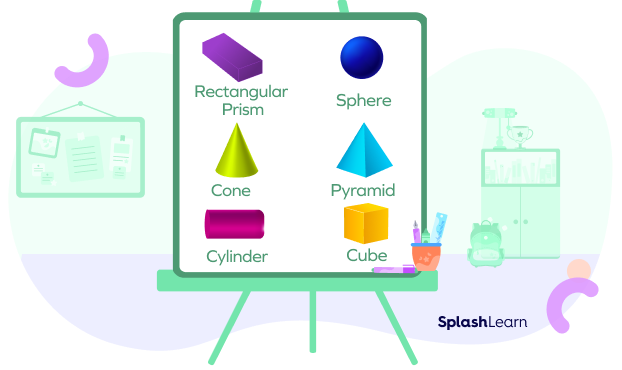
Solid Shapes
Any three-dimensional objects with length, breadth, and height are known as solid shapes. Pyramids, cuboids, cubes, and cones are examples of three-dimensional shapes. Their surfaces are called faces.
Examples:
A sphere is a solid figure with only one curved face, no edges, and no vertices.
A cone has 2 faces: one curved face and another flat circular face but only one vertex and edge each.
Another example is a cylinder that has three faces, with two edges but no vertices.
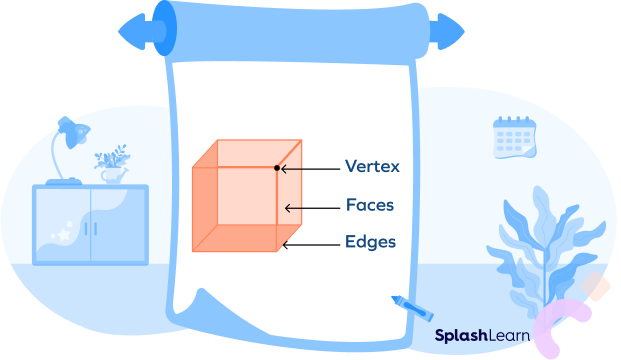
Now, let’s understand what faces, vertices, and edges are.
Dimensions of a Shape
Dimensions in mathematics are the measure of the size or distance of an object or region or space in one direction. In simpler terms, it is the measurement of the length, width, and height of anything.
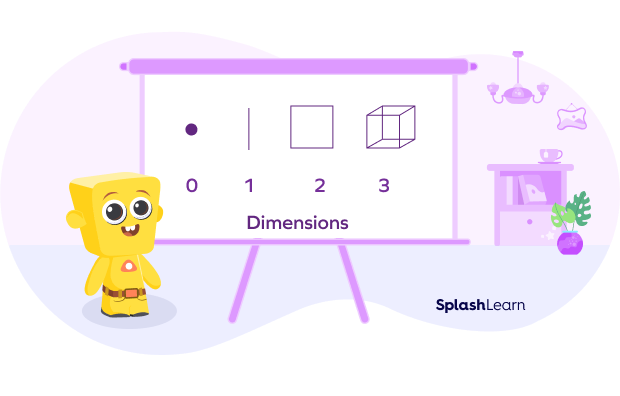
A point has no dimension.
A line is one dimensional since it only has length.
A cube is three dimensional since it has length, breadth, and height.
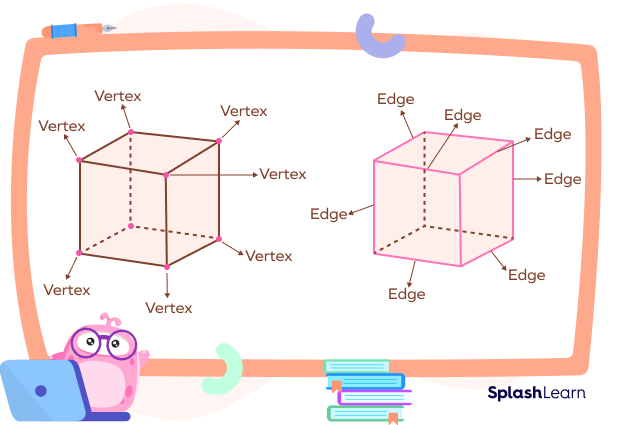
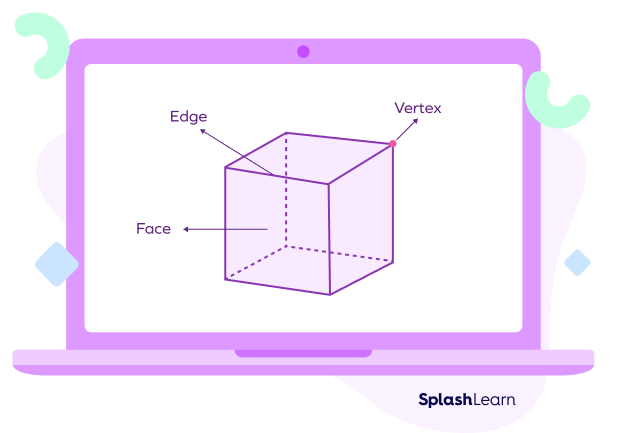
What are Vertices?
Look for the points where two or three lines meet, like the corner of a cardboard sheet or the corner of a gift box. These are examples of vertices. The point where three edges or lines meet is known as the vertex. The plural form of a vertex is vertices.
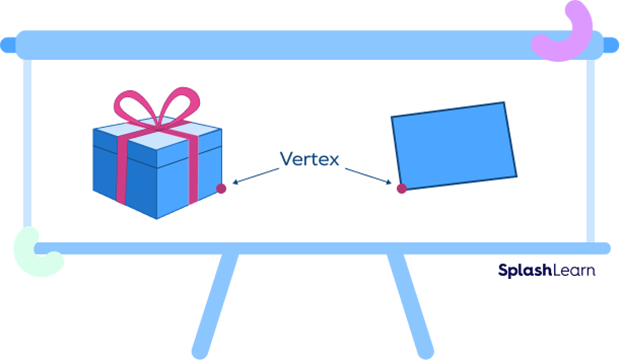
Let’s understand this with an example: A cube has 8 corners or vertices.
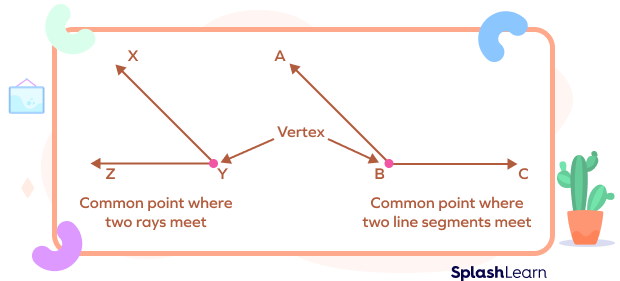
The common endpoint where two or more rays or line segments meet is called a vertex. The plural of vertex is “vertices.” Vertices are denoted by capital letters.
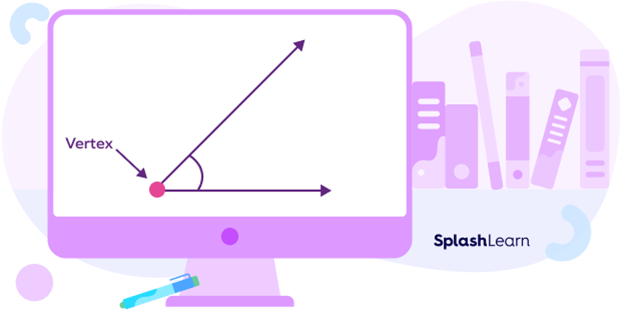
An angle is formed when two straight lines or rays meet at a common endpoint. The common point of contact is called the vertex of an angle. We can see that we are looking at the “corner” of the angle to see the vertex. Vertices are sometimes also called corners.
Vertices of 2D Shapes
2-dimensional shapes are flat shapes which have only two dimensions, length and width. Triangle, rectangle, circle are a few examples of 2D shapes. Simple, closed 2D shapes made up of only straight lines are called polygons.
The line segments that make the polygon are known as sides or edges.
The point where adjacent sides meet is called vertex.
Different shapes have different numbers of vertices. Let us see vertices of some 2D shapes.
Vertices of a Triangle
Triangle is a three-sided 2D shape or polygon.
A triangle is made up of three line segments or sides. A triangle has 3 sides, 3 vertices and 3 angles. A triangle is denoted by the symbol $\Delta$ .
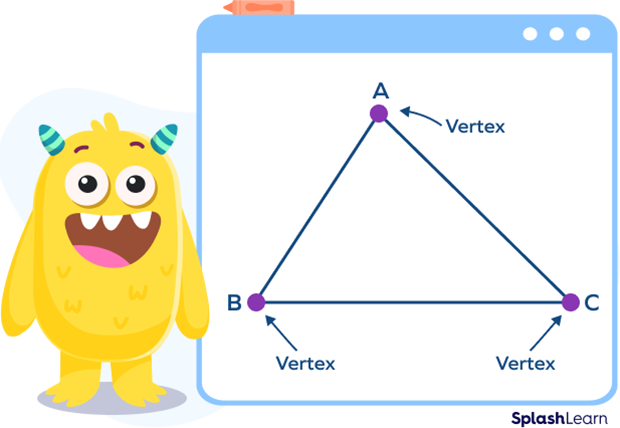
In $\Delta$ ABC, (AB, BC), (BC, CA) and (CA, AB) are adjacent sides of the given triangle.
“A”, “B”, “C” are the three vertices since the adjacent sides meet at these points.
Vertices of a Square
Square is a four sided 2D shape or polygon.
A square is made up of four line segments or sides. Adjacent sides of a square meet at a point known as vertex. A square has four sides, four vertices and four angles.
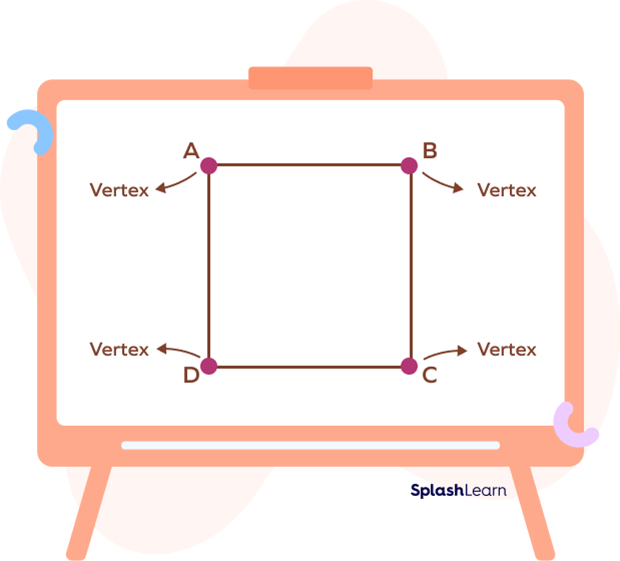
(AB, BC), (BC, CD), (CD, DA) and (DA, AB) are adjacent sides of the square.
Therefore, in square ABCD, “A,” “B,” “C,” and “D” are the four vertices.
Vertices of a Rectangle
Rectangle is a four sided 2D shape or polygon.
A rectangle is made up of four line segments or sides. Adjacent sides of a square meet at a point known as vertex. A square has four sides, four vertices and four angles.
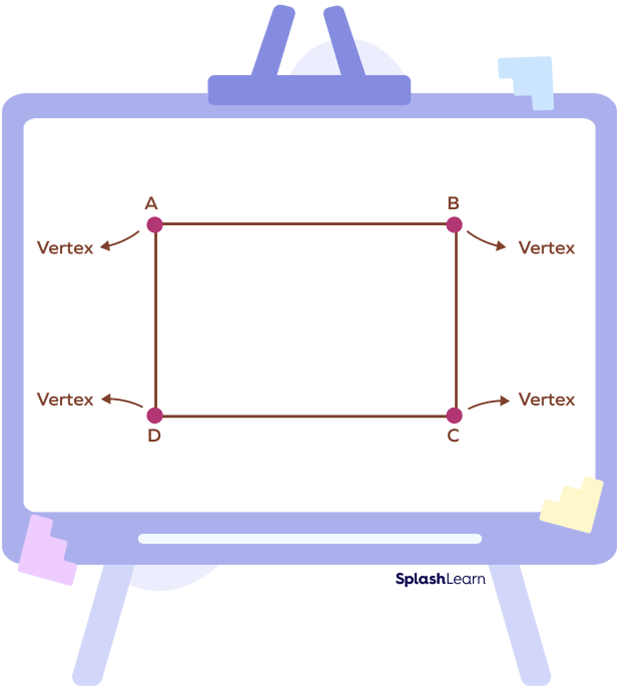
(AB, BC), (BC, CD), (CD, DA) and (DA, AB) are adjacent sides of the rectangle.
So, in the rectangle ABCD, “A,” “B,” “C,” and “D” will be the four vertices.
Vertices of a Pentagon
Pentagon is a five sided 2D shape.
A pentagon is made up of five line segments or sides. Adjacent sides of a pentagon meet at a point known as vertex. A pentagon has five sides, five vertices, and five angles.
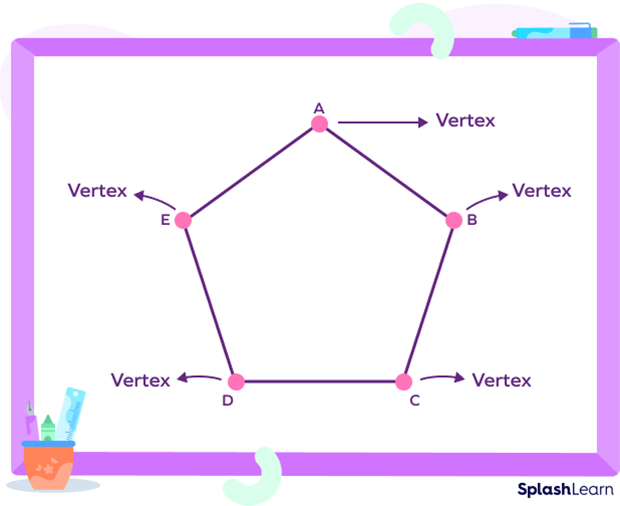
(AB, BC), (BC, CD), (CD, DE), (DE, EA) and (EA, AB) are adjacent sides of the pentagon.
So, in pentagon ABCDE, “A,” “B,” “C,” “D,” and “E” will be the five vertices.
Vertices of an Irregular Shape
The figure shown is of a pentagon with unequal sides. A polygon with unequal sides is known as an irregular polygon.
Here, too, a vertex is formed when two adjacent sides meet.
For example, in the given image, we have an irregular pentagon that has five vertices and five sides.
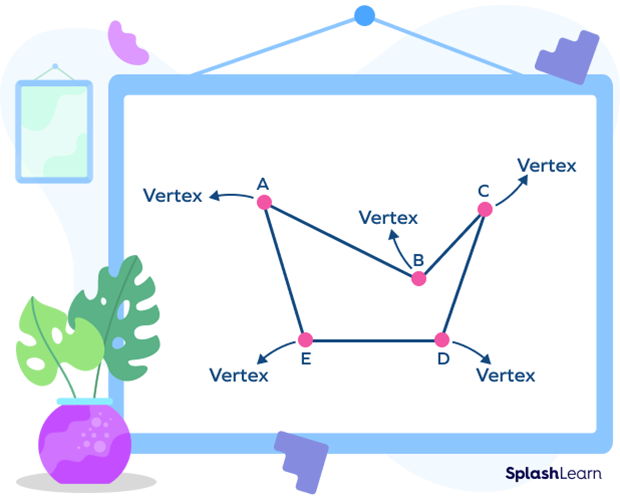
In the given irregular pentagon ABCDE, “A,” “B,” “C,” “D,” and “E” are the five vertices.
(AB, BC), (BC, CD), (CD, DE), (DE, EA) and (EA, AB) are adjacent sides of the pentagon.
Look at the table:

We can see that the number of vertices is always equal to the number of sides of a polygon.
Vertices of a Circle
A circle is a 2D shape consisting of all points in a plane that are at a given distance from a given point, the center.

A circle has infinite points on it but has zero vertices as vertex is a point where line segments or rays meet and circle has no line segments or rays.
Vertices of 3D Shapes
3D stands for 3-dimensional or three-dimensional. Three-dimensional shapes are shapes which have three dimensions: length, width, and height. Cube, pyramid, and cone are few examples of 3D shapes.
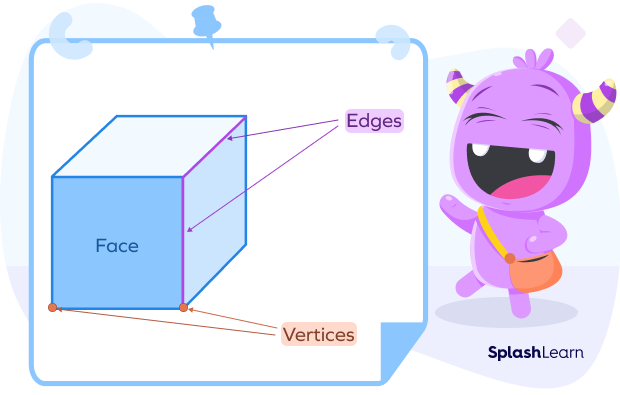
3D shapes have faces, edges and vertices.
A face is a flat or curved surface on a 3D shape.
An edge is where two faces meet.
A vertex is a point where edges meet.
Different 3D shapes have different numbers of vertices. Let us see vertices of some 3D shapes.
Vertices of a Cube
A cube is a three-dimensional solid bounded by six square faces, with three faces meeting at each vertex.
A cube has 8 vertices. 7 are visible here and one is hidden.
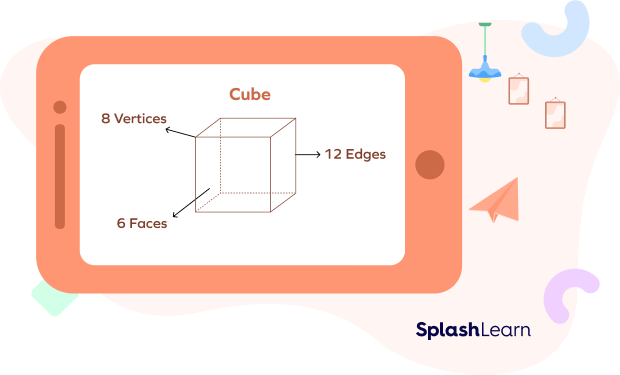
A cube has 6 faces and 12 edges.
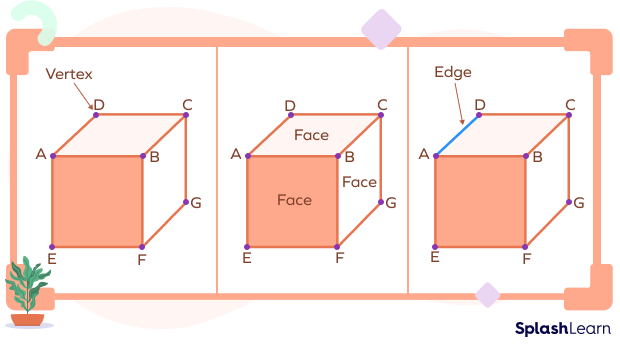
We can see in the given figure that the point where AB and AC meet is one of the vertices of the cube. Similarly, where two or more edges meet on the cube, we call that point the vertex.
Vertices of a Cuboid
A cuboid is a three-dimensional solid bounded by six rectangular faces, with three faces meeting at each vertex.
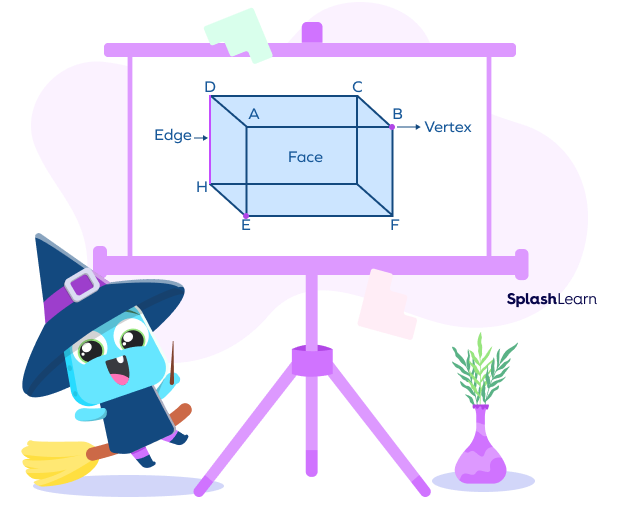
In the cuboid shown A, B, C, D, E, F, G, and H are the 8 vertices of the cuboid.
A cuboid has 8 vertices, 6 faces and 12 edges.
Vertices of a prism
A prism is a 3D shape for which the top and bottom faces are congruent polygons, and all other faces are rectangles.
In a prism, the number of vertices will be equal to twice the number of vertices in one face.
Number of vertices in a prism $= 2 \times$ Number of vertices in one face.
Let’s take an example of a triangular prism. We know that a triangle has 3 vertices.
So, the number of vertices in a triangular prism $= 2 \times$ Number of vertices in a triangle
$= 2 \times 3 = 6$
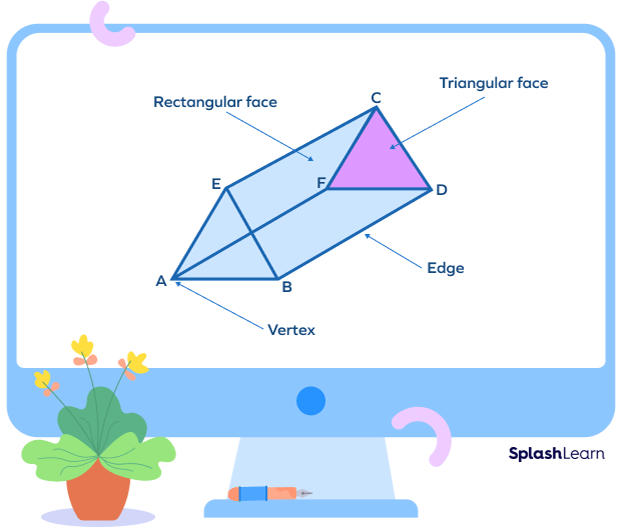
In the triangular prism shown A, B, C, D, E and F are the 6 vertices of the prism.
A triangular prism has 6 vertices, 9 edges along with 2 triangular faces (base) and 3 rectangular faces.
Vertices of a pyramid
A pyramid has a polygonal base and flat triangular faces that are joined at a common point called the vertex.
In a pyramid, the number of vertices will be equal to one more than the number of vertices in the base.
Number of vertices in a pyramid $= 1 +$ number of vertices in the base
Let’s take an example of a square pyramid. We know that a square has 4 vertices.
So, the number of vertices in a square pyramid $= 1 +$ Number of vertices in a square
$= 1 + 4 = 5$
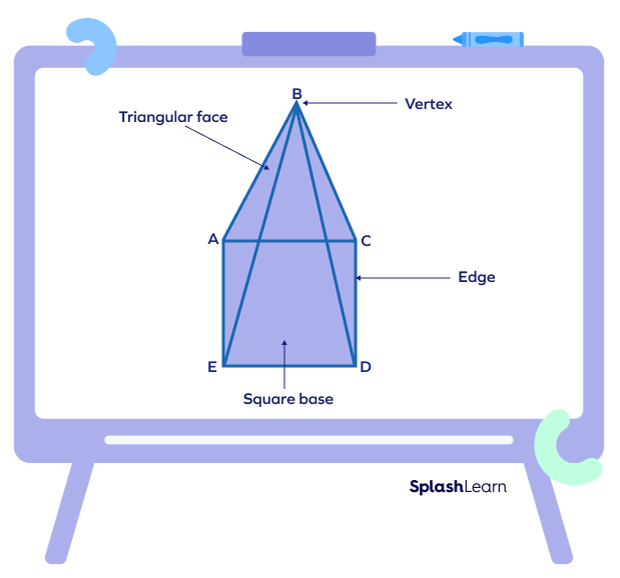
In the square pyramid shown A, B, C, D and E are the 5 vertices of the pyramid.
A square pyramid has 5 vertices and 8 edges, with 1 square face (base) and 4 triangular faces.
Special Types of 3D Shapes and Their Vertices
Vertices of a Cone
A cone is a three-dimensional figure that has a flat surface and a curved surface, pointed towards the top at the vertex. It’s a special type of figure where the base is circular and has only one vertex at the top.
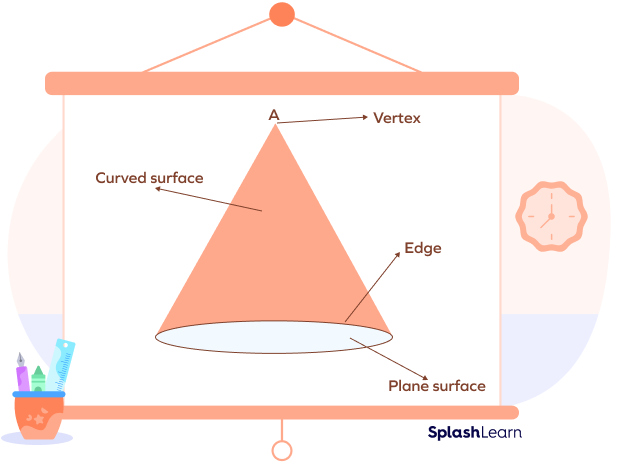
In the cone shown, A is the vertex of the cone.
A cone has 1 vertex and 1 circular edge.
A cone has 2 faces, 1 flat circular surface and 1 curved face.
Vertices of a Cylinder
A cylinder is a 3D shape consisting of two parallel circular bases that are joined by a curved surface. It has 2 circular bases that means two circular edges which are parallel and no straight lines which meet these edges. Therefore, a cylinder has no vertices.
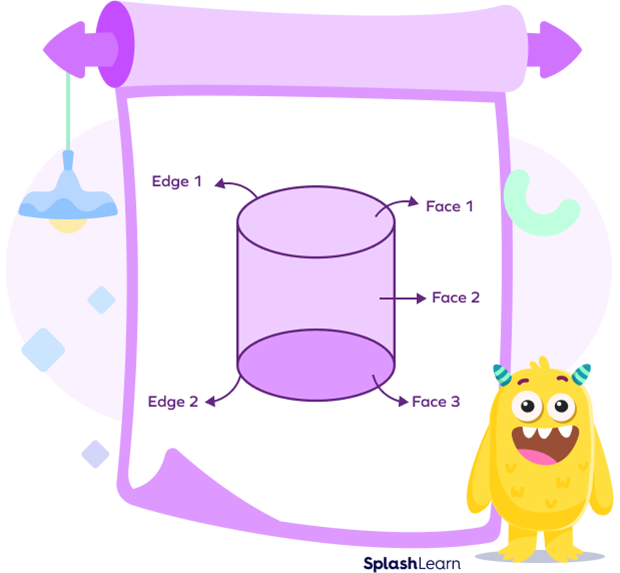
A cylinder has no vertex as it has no straight edges.
A cylinder has 3 faces, 2 flat, and 1 curved face.
A cylinder has 2 circular edges.
Vertices of a Cphere
A sphere is the set of all points in three-dimensional space lying at the same distance from a given point, center. A sphere has no edges or straight lines and only one circular surface, therefore, a sphere has no vertices.
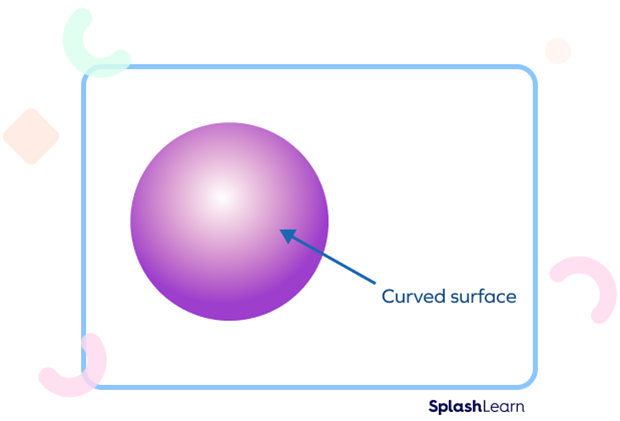
What are Faces?
A face of a solid can be defined as every single flat surface of a solid. It forms part of the boundary. In any geometric solid that is made of flat surfaces, each flat surface is called a face.
Any two dimensional shape has only one flat face.
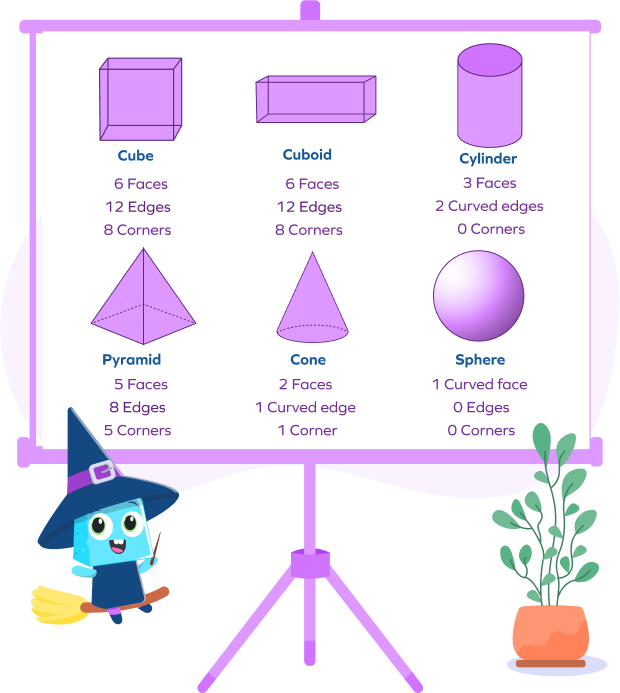
Faces of a Cube
A cube has 6 square-shaped faces.
Faces of a Cuboid
A cuboid has 6 rectangular-shaped faces, where the opposite faces are the same.
Faces of a Square Pyramid
A square-based pyramid has a square face as a base with four triangular faces on its sides.
Faces of a Cone
A cone’s base is a flat circle face with one curved face wrapping around its base.
Faces of a Sphere
A sphere has no flat faces but one complete curved face.
What are Edges?
Edges are line segments where two faces of a solid meet. Edges on a 2D shape connect two vertices.
An edge is a line that joins the corners or edges of a given shape or surface. There is a difference in how we can define edges for a two-dimensional and a three-dimensional figure.
Edges in a 2D Shapes
Any line that makes up the shape’s sides are its edges for a two-dimensional flat shape. An edge is a line segment between two faces of a solid or a line segment on a boundary?
Consider a square ABCD as shown below. A square is a 2D shape. In a 2D shape, any bounding straight edge is also called a side.
Edges in a 3D Shapes
For a three-dimensional solid, edges are those line segments where any flat sides of the object meet. We often refer to the edges as the shape’s sides. Accordingly, different shapes have different numbers of edges.
For example, a cube has 12 edges.
A cylinder is a 3D shape, and it has 2 edges.
A sphere is a perfect round, which is why it has no edges.
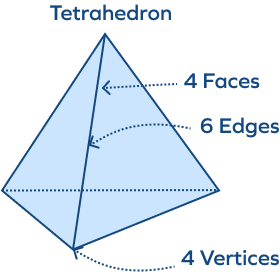
A tetrahedron has 6 edges.
A cone is a unique shape with only one edge, vertex and face.
Edges in Real Life
There are plenty of real-life examples of edges in some daily objects. We look at them almost daily, and it is easy to find them around us.
- A microwave in the shape of a cuboid has several edges. The edges may be curved or sharp straight.
- A birthday hat is conical in shape. It has only one edge.
- Just like a cube, a rolling dice has 12 edges.
Difference Between Edges and Vertices
Let us see the difference between edges and vertices.
An edge of a 3D shape is where two faces meet. They are the line segments or curved lines which make the 3D shape. But a vertex is the point where two or more edges or line segments meet.
An interesting case is that of a cylinder which has 2 edges but both of them are circular so they do not meet at a singular point, making the cycling devoid of any vertices.
Euler’s Formula
A three-dimensional shape made up of polygonal faces is known as a polyhedron. Examples of polyhedrons are cube, prism, pyramid and so on.
The relationship between vertices, edges and faces for polyhedrons can be given by Euler’s formula.
Euler’s formula says, in a polyhedron, the number of vertices (V) and faces (F) together is exactly two more than the number of edges (E).
$\text{V} + \text{F} = 2 + \text{E}$
$\text{V} + \text{F} \;−\; \text{E} = 2$
Euler’s formula is satisfied by all polyhedrons. We can also say that a 3D shape is a polyhedron if it satisfies Euler’s formula.
Example 1: Let us verify Euler’s formula for a cube.
A cube has 8 vertices, 12 edges and 6 faces.
i.e. $\text{V} = 8$
$\text{E} = 12$
$\text{F} = 6$
Euler’s formula: $\text{V} + \text{F} \;−\; \text{E} = 2$
$8 + 6 – 12 = 2$
$2 = 2$
Therefore, Euler’s formula is verified. Cube is a polyhedron.
Example 2: Square pyramid
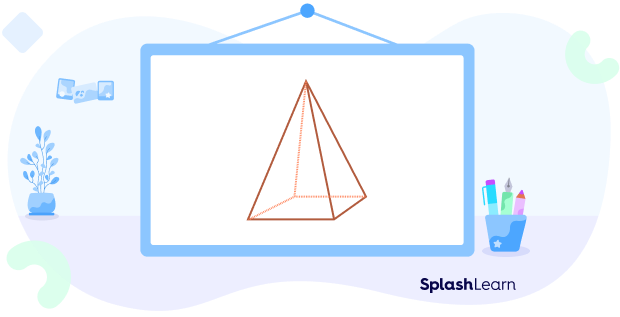
In this square pyramid, there are
4 triangular faces and 1 square face $= 5$ faces
1 vertex at the top and 4 vertices at the base $= 5$ vertices
4 slant edges and 4 edges at the base $= 8$ edges
So, using Euler’s formula,
$5 + 5 – 8 = 2$
You can also try this formula on other platonic solids, such as octahedrons, tetrahedrons, etc.
Conclusion
In this article, we learnt about vertices, edges, and faces of different shapes. Let’s solve a few examples for better understanding.
Solved Examples
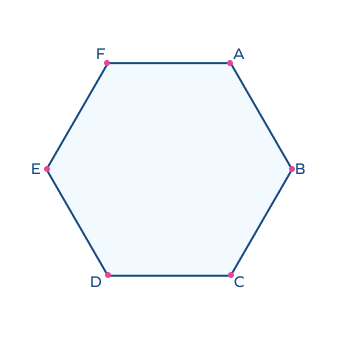
1. How many vertices are there in a hexagon?
Solution: As a hexagon is a 6-sided polygon, it will also have 6 vertices. In this hexagon, A, B, C, D, E, F are the vertices.
2. How many vertices does a rectangular prism have?
Solution:
A rectangular prism has 8 vertices.
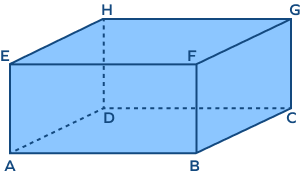
A, B, C, D, E, F, G, H are the vertices of the above rectangular prism.
3. How many vertices does a triangular pyramid have?
Solution:
A triangular pyramid had 4 vertices.
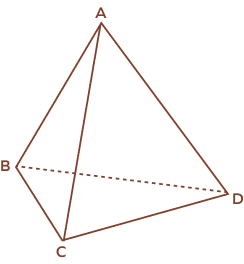
A, B, C and D are the vertices of a triangular pyramid shown above.
4. Verify Euler’s formula for a pentagonal pyramid.
Solution:
A pentagonal pyramid is a three-dimensional shape with a pentagonal base and upon which are five triangle-shaped lateral sides that meet at the vertex.
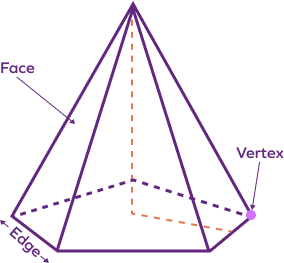
Pentagonal pyramid has 6 vertices
Pentagonal pyramid has 10 edges
Pentagonal pyramid has 6 faces
Euler’s formula: $\text{V} \;−\; \text{E} + \text{F} = 2$
$6 \;–\; 10 + 6 = 2$
$2 = 2$
Hence, Euler’s formula is verified for a pentagonal pyramid.
5. Can you tell how many vertices a hexagonal pyramid will have, without counting?
Solution:
Vertices of a pyramid $= 1 +$ Vertices of the base
A hexagonal pyramid will have a hexagon as its base
So, Vertices of a hexagonal pyramid $= 1 +$ vertices of hexagon
$= 1 + 6 = 7$
6. How many faces, vertices, and edges are present in a pentagonal prism?
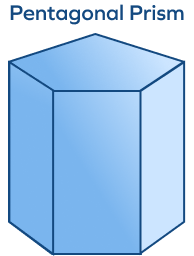
Solution:
This pentagonal prism has 7 faces, 10 corners, and 15 edges.
7. How faces, vertices and edges does a tetrahedron have?
Solution:
A tetrahedron has 4 flat surfaces, all of which are triangular in shape, 6 edges and 4 vertices.
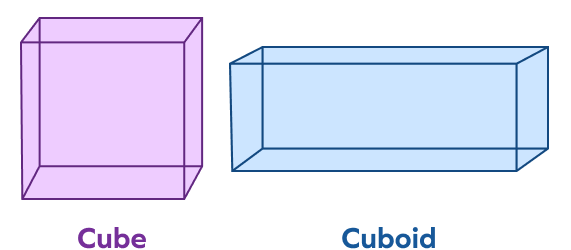
8. What is the difference between a cube and a cuboid in terms of faces, vertices and edges? Explain their dimensions.
Solution:
Both cubes and cuboids are three dimensional in shape with mutually right-aligned surfaces. Both shapes have 6 faces, 12 edges, and 8 vertices.
If we talk about differences, then all 6 faces of the cuboid are rectangular, but all 6 faces of the cube are square.
A cuboid’s length, breadth, and height are not the same, but in a cube, all the 3 dimensions are the same.
So all cubes are cuboids, but all cuboids may or may not be cubes.
9. Is a cylinder a solid shape or a plane shape? How many faces, vertices and edges does a cylinder have?
Solution:
A cylinder is a three-dimensional object with two identical, circular faces at each end, one curved side and no edges or vertices.

10. How will you prove Euler’s Formula for a tetrahedron?
Solution:
We know that a tetrahedron is a polygon with 4 faces, 4 vertices, and 6 edges. According to Euler’s Formula, $\text{F} + \text{V} = \text{E} + 2$
- $4 + 4 = 6 + 2$
- $8 = 8$
- Hence Proved.
11. The edge of a square is 10 feet. What will be the perimeter?
Solution:
The perimeter of the square shape will be the sum of its four sides.
Assuming that the square is a two-dimensional shape, we know that the perimeter equals the sum of all edges of the shape.
Perimeter $= 10\; ft + 10\; ft + 10\; ft + 10\; ft = 40\; ft$
12. The edge of a cube is 12 cm. What will be its perimeter?
Solution:
Perimeter of a cube $=$ Number of edges $\times$ Length of each edge.
Also, we know that number of edges in a cube $= 12$.
Perimeter of a cube $= 12 \times 12$
Perimeter of a cube $= 144$ cm
13. A cube has 6 faces and 12 edges, what will be the number of its vertices according to Euler’s Formula?
Solution:
The number of vertices will be 8.
According to Euler’s Formula, $\text{F} + \text{V} = \text{E} + 2$
$6 + \text{V} = 12 + 2$
$\text{V} = 12 + 2 \;–\; 6$
$\text{V} = 8$
14. To draw a square and a triangle on paper, how many total edges will we have to draw?
Solution:
We will draw a total of 7 edges.
A square has 4 edges.
A triangle has 3 edges.
Hence, to draw a square and a triangle on paper, we have to draw 7 edges.
Practice Problems
Vertices, Faces And Edges
How many vertices does an octagon have?
An octagon has 8 vertices.
How many vertices does the given irregular polygon have?
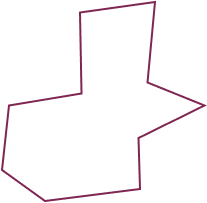
The given irregular polygon has 10 vertices.
How many vertices does a pentagonal prism have?
A pentagonal prism has 10 vertices.
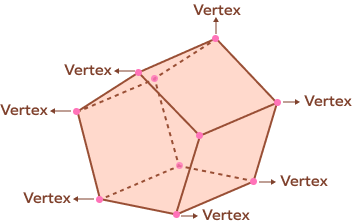
A polyhedron has 12 edges and 6 faces, find the number of vertices.
Euler’s formula is $\text{V} \;−\; \text{E} + \text{F} = 2$
$\text{V} \;–\; 12 + 6 = 2 ; \text{V} = 8$
Which of the following 3D shape has:
Faces: 5
Edges: 9
Vertices: 6
A triangular prism has 5 faces, 9 edges, and 6 vertices.
Which among these below is Euler's formula?
There are always relationships between faces, vertices, and edges. This relationship is explained by the formula, $\text{F} + \text{V} \;-\; \text{E} = 2$ (Here, $\text{F} =$ faces, $\text{V} =$ vertices, $\text{E} =$ edges)
What type of faces does a cone have?
A cone has 2 faces: one curved face and another flat circle face.
How many edges does a cone have?
A cone has only one curved edge.
Which of the following solids has the least number of faces?
Triangular pyramids have only 4 faces, whereas other pyramids have 5 faces.
If the number of faces of a cube is 6 and vertices is 8, find out the number of edges according to Euler's formula.
According to Euler’s Formula, $\text{F} + \text{V} = \text{E} + 2$
$6 + 8 = \text{E} + 2$
$14 = \text{E} + 2$
$14 \;–\; 2 = \text{E}$
$\text{E} = 12$.
Which of the following solid shapes do not have any edges?
A cube has 12 edges, a prism has 9 edges, and a pyramid has 6 edges, but a sphere does not have any edge since it is one plain round ball-like shape.
Which of the following shapes have a curved edge?
A cone is the only shape out of the given options with a curved edge in the shape of a circle.
What do we call a point where two or more edges meet?
A point where two edges meet in a given shape is a Vertex. A face is a side of a shape, and an edge is a line segment that joins one vertex to another.
If the edges of a triangle are 12 in, 14 in, and 12 in, what will be its perimeter?
The perimeter of a two-dimensional shape is the sum of all the edges.
Perimeter $= 12 + 14 + 12$
Perimeter $= 38$ in
Frequently Asked Questions
How many vertices does an octahedron have?

An octahedron is a shape that is formed by joining two square pyramids at their bases. It has 6 vertices.
Is Euler’s formula true for shapes with curved surfaces?
No, Euler’s formula only stands true for polyhedrons. For example, a cylinder is not a polyhedron, so the Euler’s formula does not stand true for the cylinder. Let’s understand how with the given figure.
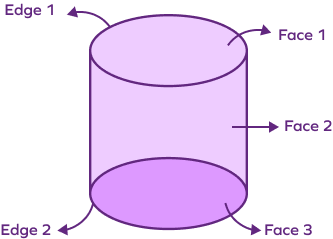
A cylinder has 0 vertices, 2 edges, and 3 faces.
Euler’s formula: $\text{V} \;−\; \text{E} + \text{F} = 2$
$0 \;–\; 2 + 3 \neq 2$
$1 \neq 2$
Is Euler’s rule satisfied for a sphere?
The number of vertices of a sphere is zero.
The number of edges of a sphere is zero.
The number of faces of a sphere is one.
Euler’s formula is $\text{V} \;−\; \text{E} + \text{F} = 2$
$0 \;-\; 0 + 1 \neq 2$
$1 \neq 2$
Euler’s rule is not satisfied for a sphere as it is not a polyhedron.
Are the number of vertices equal to the number of sides for all two-dimensional shapes?
The number of vertices is equal to the number of sides only for two-dimensional polygons like triangles, squares, pentagons etc. They are not equal for two-dimensional shapes like circle and oval as they are not polygons.
What is the difference between a vertex and an angle?
Both, a vertex and an angle are formed when two rays or line segments meet. An angle is the measure of the inclination of the two rays whereas the vertex is the point of intersection of the two rays.
Which solid space has no edges?
Spheres have no edges as they have only one curved face.
What are polyhedrons?
Polyhedrons are three-dimensional solids that have flat polygonal faces, sharp vertices, and straight edges. Some examples of solid shapes that are polyhedrons are pyramids, cubes, and prisms.
What does Euler’s formula define?
Euler’s formula shows the relationship between faces, edges, and vertices of polyhedrons. According to the formula, the number of faces + the number of vertices $–$ the number of edges $= 2$.
What is the difference between 2D and 3D shapes?
Three-dimensional shapes have three dimensions: length, breadth, height.
Two-dimensional shapes only have a breadth and length.
Some examples of 3D shapes are spheres, pyramids, cuboids, and prisms, whereas 2D shapes are squares, triangles, circles, etc.
How do a vertex, edge, and face look different from each other?
A vertex is a corner, an edge is a straight line, and a face is a surface.
What is the Euler theorem?
The Euler theorem is among the most important mathematical theorems. According to the theorem, for polyhedrons, the number of faces plus the number of vertices minus the number of edges is equal to 2.
How are a cube and cuboid similar in terms of the number of edges?
Both cubes and cuboids are a type of prism and have 12 edges each.
Do all shapes have only straight lines for edges?
No, all shapes don’t need to have straight lines for edges. Shapes like a hemisphere can have a curved edge.
How many faces does a 2D shape have?
Any two-dimensional shape has only one face bounded by its sides.























