What is a Fraction?
Fractions represent the parts of a whole or collection of objects. A fraction has two parts. The number on the top of the line is called the numerator. It tells how many equal parts of the whole or collection are taken. The number below the line is called the denominator. It shows the total number of equal parts the whole is divided into or the total number of the same objects in a collection.
Fraction of a Whole
When the whole is divided into equal parts, the number of parts we take makes up a fraction.
If a cake is divided into eight equal pieces and one piece of the cake is placed on a plate, then each plate is said to have $\frac{1}{8}$ of the cake. It is read as ‘one-eighth’ or ‘1 by 8’
Fraction of a Collection of Objects
There are a total of 5 children.
3 out of 5 are girls. So, the fraction of girls is three-fifths ( $\frac{3}{5}$ ).
2 out of 5 are boys. So, the fraction of boys is two-fifths ( $\frac{2}{5}$ ).
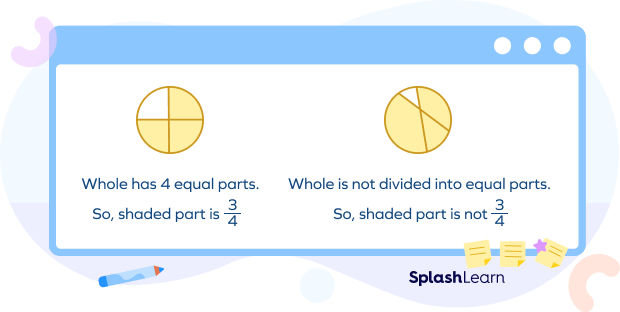
Equal and Unequal Parts
To identify the fraction, the whole must be divided into equal parts.
Representing a Fraction
A fraction can be represented in 3 ways: as a fraction, as a percentage, or as a decimal. Let us see each of the three forms of representation.
Fractional Representation,
The first and most common form of representing a fraction is in the form ab. Here, a is called the numerator and b is called the denominator. Both the numerator and denominator are separated by a line.
Example: We can understand the fraction $\frac{3}{4}$ as follows.
Numerator: 3
Denominator: 4
The fraction represents three parts when a whole is divided into four equal parts.
Decimal Representation
In this format, the fraction is represented as a decimal number.
Example: The fraction $\frac{3}{4}$ can be shown as a decimal by dividing the numerator (3) by the denominator (4). $\frac{3}{4}$ = 0.75.
Thus, in decimal representation, $\frac{3}{4}$ is written as 0.75.
Percentage Representation
In this representation, a fraction is multiplied by 100 to convert it into a percentage.
Example: If we want to represent as a percentage, we should multiply $\frac{3}{4}$ by 100.
$\frac{3}{4}$ x 100 = 0.75 x 100 = 75. Thus, we can represent $\frac{3}{4}$ as 75%.
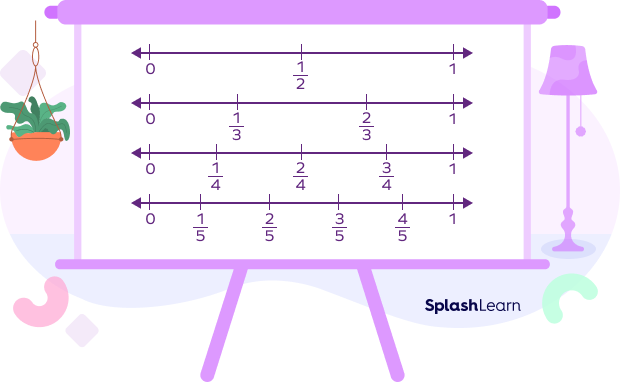
Fractions on Number Line
Fractions can be represented on a number line, as shown below.
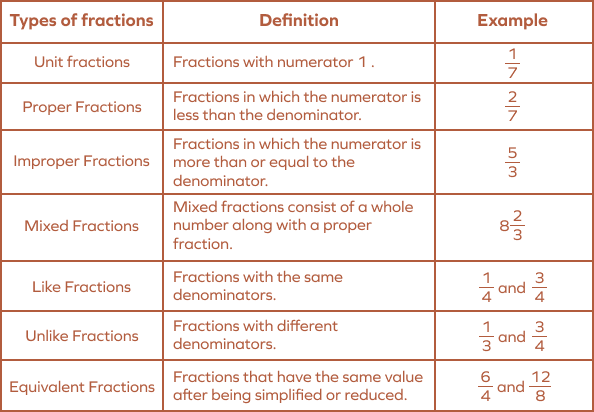
Types of Fractions
The primary parts of a fraction are the numerator and the denominator. Based on these, different types of fractions can be defined. Let us look at some common types of fractions.
Mixed Fractions to Improper Fractions
Mixed fractions can be converted to improper fractions by multiplying the whole number by the denominator and adding it to the numerator. It becomes the new numerator and the denominator remains unchanged.
Example: 8$\frac{2}{3}$ = $\frac{(8 \times 3) + 2}{3}$ = $\frac{26}{3}$
Conclusion
The easiest way to teach this topic to kids is by helping them visualize the fractions. This can be done with the help of paper cutouts or interactive online games like the ones available on https://www.splashlearn.com/fraction-games. Check the Splashlearn website for more such fun ways to learn different mathematical concepts.
Solved Examples
1. Convert the mixed number 4$\frac{3}{5}$ to an improper fraction.
Solution: 4$\frac{3}{5}$ = $\frac{(4 ✕ 5) + 3}{5}$ = $\frac{20 + 3}{5}$ = $\frac{23}{5}$
2. Are the fractions $\frac{14}{20}$ and $\frac{7}{10}$ equivalent?
Solution:
Simplest form of $\frac{14}{20}$ = $\frac{7}{10}$
Simplest form of $\frac{7}{10}$ = $\frac{7}{10}$
Since the simplest form of both the fraction is $\frac{7}{10}$, we can say that two fractions are equivalent.
3. From the following fractions separate proper fraction and improper fraction
$\frac{9}{2}$, $\frac{4}{11}$, $\frac{16}{16}$, $\frac{2}{3}$, $\frac{7}{9}$, $\frac{5}{6}$
Solution:
Proper fraction: $\frac{4}{11}$, $\frac{2}{3}$, $\frac{7}{9}$, $\frac{5}{6}$
Improper fraction: $\frac{9}{2}$, $\frac{16}{16}$
4. Convert $\frac{2}{5}$ as a percentage.
Solution:
$\frac{2}{5} \times 100%$ = 40%
Practice Problems
Fractions
1Which of the following is an improper fraction?
$\frac{18}{11}$ is an improper fraction since the numerator (18) is greater than the denominator (11).
2Which of the following is the decimal representation of the fraction $\frac{3}{8}$?
Dividing the numerator (3) by the denominator (8) gives the decimal number 0.375.
3What value of x will make the following two fractions equivalent?
$\frac{3}{7}$ and $\frac{x}{21}$
$\frac{(3 ✕ y)}{(7 ✕ y)}$ = $\frac{x}{21}$
Now, solve for 7 x y = 21. We know that y = 3. Thus, the numerator should be 3 x 3 = 9.
4What type of fraction is $\frac{2}{5}$?
Since the numerator is less than the denominator, the given fraction is a proper fraction.
Frequently Asked Questions
What is the easiest way to identify if a number can be converted to a mixed fraction?
The simplest way to identify this is by comparing the numerator with the denominator. If the numerator is greater than the denominator, the fraction is improper and can be converted into a mixed fraction.
Are there any real-life examples where fractions are used?
Fractions are very common in everyday life. Whether we are shopping for groceries or baking a cake, celebrating a party or calculating the budget at the beginning of the month, fractions are used.
What is a proper fraction?
Proper fractions are fractions in which the numerator is less than the denominator. Decimal value of a proper fraction is always less than 1.
Where are Equivalent fractions useful?
Equivalent fractions help in a number of scenarios where calculations include fractional numbers. For example, addition, and subtraction of fractions become very easy when equivalence properties of fractions are used.