What Is the Denominator of a Fraction?
A denominator is the bottom number in a fraction. A denominator is a number below the horizontal bar of a fraction.
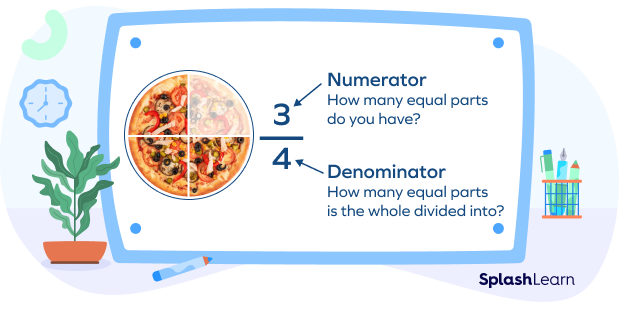
A fraction represents a part of a whole. If you divide a pizza into 4 equal parts, each part represents a fraction $\frac{1}{4}$. Three parts represent the fraction $\frac{3}{4}$. Here, 4 is the denominator of the fraction and it represents the total number of parts the whole is divided into.
Recommended Games
Denominator: Definition
Denominator of a fraction is the part of a fraction (a number) written below the horizontal bar of the fraction. It represents the total parts of a whole.
A fraction is of the form $\frac{a}{b},\; b \neq 0$ and both a and b are whole numbers. Here, b is the denominator. Note that a denominator can never be zero!
Fraction and denominator examples:
| Fractions | Denominator |
|---|---|
| $\frac{1}{2}$ | 2 |
| $\frac{3}{5}$ | 5 |
| $\frac{x}{y}$ | y |
| $\frac{5}{9}$ | 9 |
Recommended Worksheets
Parts of a Fraction: Numerator and Denominator
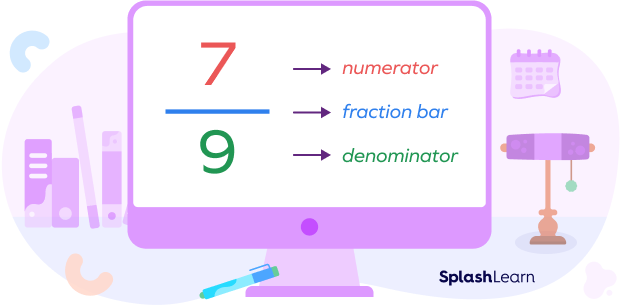
Numerator: The number written above the fraction bar is known as numerator.
It defines the number of parts of the whole we have taken.
Denominator: The number that’s written below the fraction bar is known as denominator.
It defines the total parts the whole is divided into.
The fraction bar is the small horizontal line between the numerator and denominator. It is known as “vinculum.”
Properties of a Fraction
- If two fractions have the same numerator, the fraction with the larger denominator is the smaller fraction.
Example: $\frac{2}{99} \lt \frac{2}{5}$
- If two fractions have the same denominator, the fraction with the larger numerator is the larger fraction.
Example: $\frac{2}{99} \lt \frac{7}{99}$
Denominator > Numerator
When the numerator is less than the denominator, the fraction is called a proper fraction.
Examples: $\frac{3}{4},\; \frac{4}{5},\; \frac{5}{7}$
Denominator Numerator
When the numerator is greater than (or equal to) the denominator, the fraction is called an improper fraction.
Examples: $\frac{7}{4},\; \frac{23}{5},\; \frac{15}{7},\; \frac{8}{8} = 1$
Types of Fractions Based on the Denominator
Two or more fractions are categorized as “like fractions” and “unlike fractions” based on the value of the denominators.
Fractions with Like Denominators
Observe the fractions $\frac{3}{7},\; \frac{4}{7}$ and $\frac{5}{7}$. We see that they all have the same denominator, 7. These fractions are called fractions with like denominators. The fractions with same or like denominators are called the like fractions.
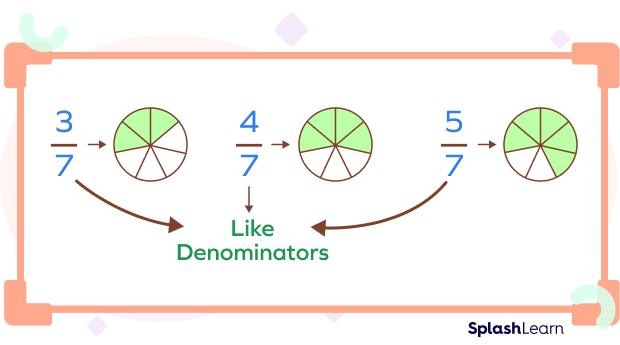
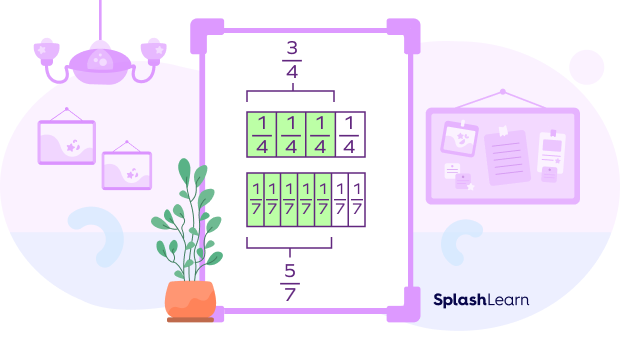
In the figure above, the denominator in all the free fractions is the same, i.e., 4. So, the denominators are like denominators.
To compare like fractions, we only compare numerators since the denominator is the same.
Example: $\frac{3}{7} \lt \frac{4}{7} \lt \frac{5}{7}$ since $3 \lt 4 \lt 5$
Fractions with Unlike Denominators
When two or more fractions have different denominators, then the fractions are called unlike fractions or fractions with unlike denominators.
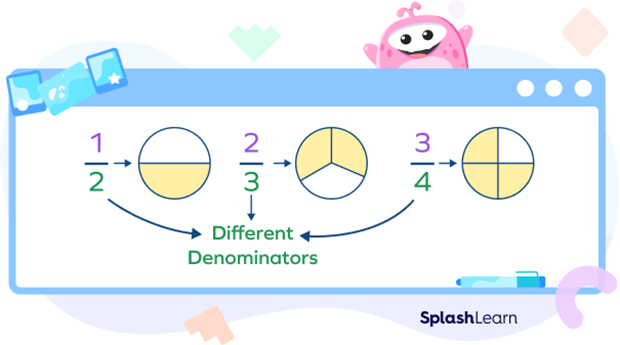
To compare, add, or subtract unlike fractions, we first need to make the denominators of all the fractions the same. In order to do this, we can use the LCM method or fraction bar models.
For example, to compare the fractions $\frac{3}{4}$ and $\frac{5}{7}$, we first draw the fraction models and then compare the two fractions. You can compare the shaded regions and conclude that $\frac{3}{4} \gt \frac{5}{7}$
Least Common Denominator
The smallest or the least number among all the common multiples of the denominators of the given set of fractions is known as the Least Common Denominator or Lowest Common Denominator.
Note that the least number of the common multiples of the denominators simply means the LCM of the denominators. Thus, to find the LCD of the given fractions, we have to calculate the LCM of the denominators. Let’s understand how to calculate LCD.
How to Find the Least Common Denominator
To find the least common denominator, we can list the multiples of both the denominators and identify the smallest common multiple. This method is convenient to use when the denominators are small numbers.
For example, $\frac{3}{4}$ and $\frac{5}{6}$.
The multiples of $4 = 4,\; 8,\; 12,\; 16,\; 20,\; 24$, …
The multiples of $6 = 6,\; 12,\; 18,\; 24$, …
Common multiples $= 12,\; 24,\; 36$, …
LCM of denominators$ = 12$
Thus, the least common denominator is 12.
Now, we will make the denominators the same (12).
$\frac{3 \times 3}{4 \times 3} = \frac{9}{12}$
$\frac{5 \times 2}{6 \times 2} = \frac{10}{12}$
Thus, we get the like fractions $\frac{9}{12}$ and $\frac{10}{12}$.
Note: If the two or more denominators have $HCF = 1$, simply multiply the denominators.
For example, $\frac{1}{9}$ and $\frac{4}{7}$.
On multiplying the denominators, we get $LCD = 9 \times 7 = 63$.
The like fractions will be $\frac{7}{63}$ and $\frac{36}{63}$.
Denominator in Division
In division problems, we divide a quantity or a number into equal parts.
The division of a number “a” by a number “b” $(b\neq 0)$ can be represented in different ways, such as $a \div b$ or a/b or$\frac{a}{b}$.
Here, the denominator “b” represents the divisor. It’s the number by which we divide another number.
Example: Divide 15 by 3.
$15 \div 3 = \frac{15}{3} = 5$
Here, 3 is the denominator. This is equivalent to dividing 15 objects into equal groups of 3.
Denominator in a Ratio
Using ratios, we compare quantities of the same kind. A ratio tells us how many times one number contains another.
In a ratio a : b, the first number “a” is called the numerator or “the antecedent,” and the second number “b” is called the denominator or the “consequent.”
Facts about Denominator
- Denominator of a fraction can never be 0.
- The term denominator in math is used in different concepts such as ratio and proportion, fractions, division problems, etc.
- If the denominator of a fraction is 1, it is called an improper fraction. Its value is the value of the numerator.
Example: $\frac{5}{1} = 5$
Conclusion
In this article, we learned about denominators, types of fractions based on the value of the denominators. Denominator is the part of the fraction below the fractional bar. Let’s solve a few examples and practice problems.
Solved Examples on Denominator
1. An apple is cut into 8 equal pieces. Pam eats 3 pieces. Express the fraction of the apple Pam had. What is the denominator? What does it represent?
Solution:
Total number of equal pieces of apple $= 8$
So, denominator $= 4$
Number of slices Pam had$ = 3$
So, numerator $= 1$
Fraction of apple Pam had $= 38$
Here, the denominator represents the total number of parts the whole apple is divided into.
2. What is the least common denominator of $\frac{3}{7}$ and $\frac{2}{5}$?
Solution:
Given fractions $= \frac{3}{7}$ and $\frac{2}{5}$
Denominators $= 5$ and 7
5 and 7 are co-prime. So, we multiply them to find the LCD.
Least common denominator $= 5 \times 7 = 35$
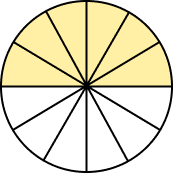
3. Identify the fraction represented by the shaded portion. What is the denominator of the fraction?
Solution:
The circle is divided into 12 equal parts, out of which 6 parts are shaded.
Thus, the shaded portion represents the fraction $\frac{6}{12}$.
The denominator of the fraction $\frac{6}{12}$ is 12. It represents the total number of equal parts of the circle.
Practice Problems on Denominator
Denominator - Definition, Examples, Facts, FAQs
Which of the following statements is NOT true about the denominator?
Denominator cannot be 0.
Which of the following fractions have unlike denominators?
The denominator of $\frac{9}{11}$ is 11 and the denominator of $\frac{1}{10}$ is 10.
What is the denominator of the fraction represented by the shaded part?
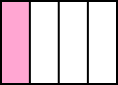
1 part is shaded out of 4 equal parts. Thus, the shaded part represents the fraction $\frac{1}{4}$.
The denominator is 4.
Frequently Asked Questions on Denominator
Can a denominator be 0?
No, a denominator cannot be zero because a fraction becomes undefined if the denominator has the value 0. We can not divide a whole into 0 equal parts.
What is a unit fraction?
A unit fraction is a fraction whose numerator is 1.
What is the fraction called when the denominator is greater than the numerator?
The fraction in which the denominator is greater than the numerator is known as improper fraction.
What does it mean when the numerator and denominator are equal?
If the numerator and denominator have the same value, the fraction becomes 1. We categorize such a fraction as an improper fraction since the numerator is not less than the denominator. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.




































