Unit Fraction – Definition, Examples, Practice Problems

Unit Fraction – Introduction

In mathematics, fractions represent a part of a whole thing, region, or collection. In other words, a fraction is a numerical value that depicts a portion or section of an entire quantity that can be a number, a certain value, or a thing. 

Every fraction includes a numerator and a denominator, separated by a horizontal line called the fractional bar.

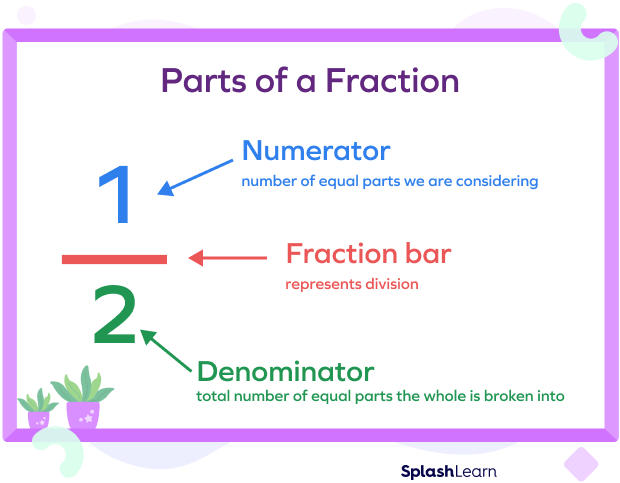
Based on the value of the numerator and denominator, fractions are categorized under several types, like an improper fraction, proper fraction, unit fraction, etc. 

What Is a Unit Fraction?

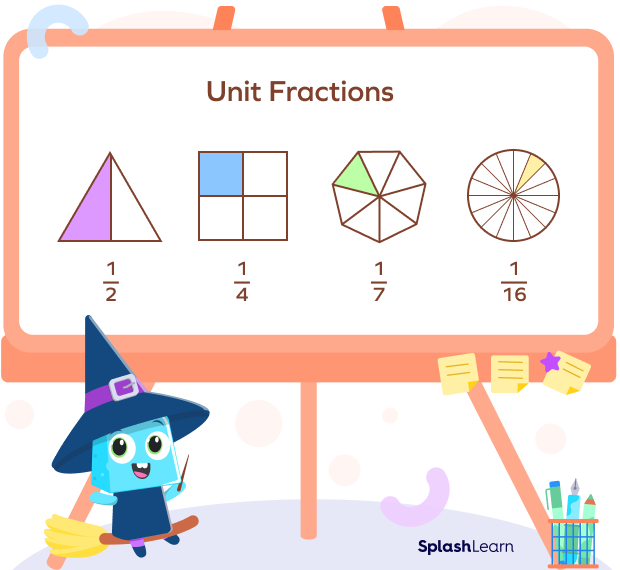
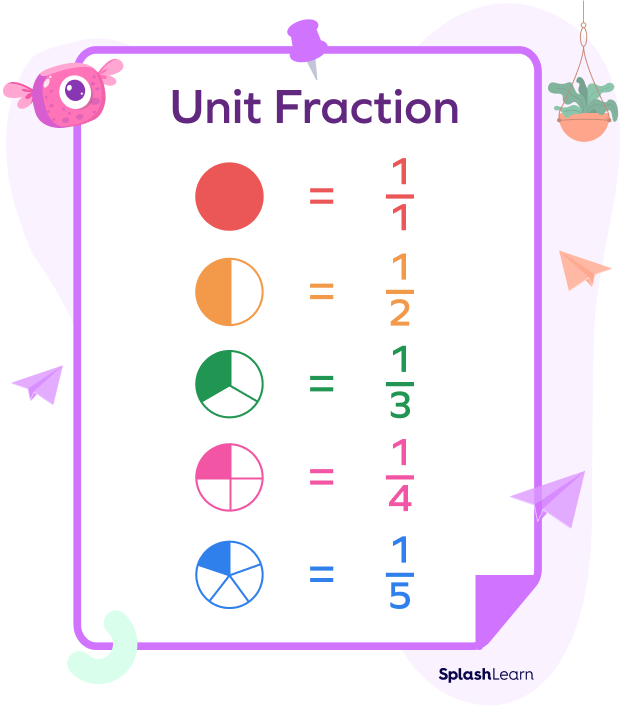
In math, a unit fraction can be defined as a fraction whose numerator is 1. It represents 1 shaded part of all the equal parts of the whole.  The term “unit” means one.

For instance, if a pizza is divided into 4 equal portions and one person is eating one portion of it, it can be numerically represented as 1/4.

If a whole is divided into three equal parts, each part is represented by the fraction 1/3, written as one-third of the whole. 

Similarly, if a whole is divided into four or five equal parts, each part is represented by the fraction 1/4 or 1/5, written as one-fourth or one-fifth of the whole.

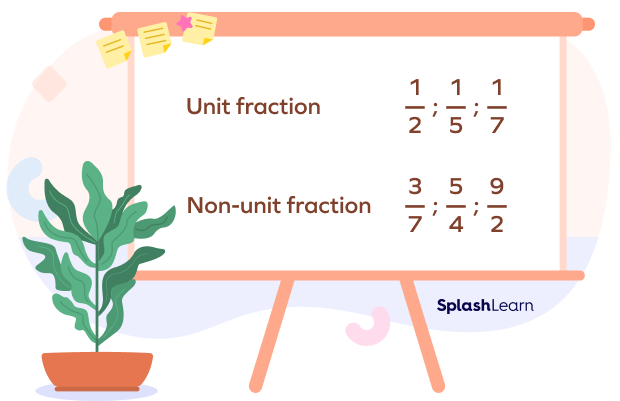
Difference Between Unit and Non-unit Fraction

While a unit means one, a non-unit represents any number other than one. Hence, a non-unit fraction is a fraction with a numerator other than one. The denominator can be any whole number except 0. Examples: 2/3, 3/5, 4/7, etc.

How to Multiply Unit Fractions

A unit fraction can be multiplied with other unit fractions, non-unit fractions, or a whole number. 

Multiplying Unit Fractions with Unit Fractions

We simply multiply the numerator with the numerator and the denominator with the denominator. 

For example, let’s multiply $\frac{1}{3}$ and $\frac{1}{4}$.

$\frac{1}{3}  \times \frac{1}{4} = \frac{1 \times 1}{3 \times 4} =\frac{1}{12}$

Multiplying Unit Fractions with Non-unit Fractions

We simply multiply the numerator with the numerator and the denominator with the denominator. We simplify the result only if necessary.

For example, let’s multiply $\frac{1}{2}$ and $\frac{3}{5}$.

$\frac{1}{2}  \times \frac{3}{5} = \frac{1 \times 3}{2 \times 5} = \frac{3}{10}$

How to Add Unit Fractions

Let’s understand how to add unit fractions with 

i) same denominators 

ii) different denominators

With the Same Denominators

Here, we only add the numerators and place the resulting sum over the common denominator. Then, we simplify our results if necessary.

For example: Let’s add $\frac{1}{4}$ and $\frac{1}{4}$.

$\frac{1}{4} + \frac{1}{4}$

$= \frac{1 + 1}{4}$

$= \frac{2}{4}$

$= \frac{1}{2}$ 

With Different Denominators

Let’s say we need to add $\frac{1}{4}$ and $\frac{1}{5}$. Here’s how to do it:

Step 1: Identify the least common multiple of the denominators.

Identify the least common denominator (LCD) of the given fractions. 

For that, we list the multiples of each denominator until we find the first common one.

Multiples of 4 = 4, 8, 12, 16, 20, 24 . . .

Multiples of 5 = 5, 10, 15, 20 . . .

So, the least common multiple here is 20.

Step 2: Convert each fraction to an equivalent fraction with the least common multiple as the denominator.

Here, the LCM is 20. 

To convert $\frac{1}{4}$ to a denominator with 20, we will have to multiply the fraction by $\frac{5}{5}$.

$\frac{1}{4}  \times \frac{5}{5} = \frac{5}{20}$

To convert $\frac{1}{5}$ to a denominator with 20, we will have to multiply the fraction by \frac{4}{4}$.

$\frac{1}{5}  \times \frac{4}{4} = \frac{4}{20}$

Step 3: Add the fraction using the equivalent fractions and simplify.

Now, the denominator of both the fractions is the same. So, we add the numerators of the like fractions and place the resulting sum over the common denominator.

$\frac{1}{4} + \frac{1}{5}$

$= \frac{5}{20} + \frac{4}{20}$

$= \frac{5 + 4}{20}$

$= \frac{9}{20}$

How to Subtract Unit Fractions

The process of subtraction is similar to the addition, but instead of adding the numerators in step 3, we subtract them here and simplify the answer.

For example, let’s subtract $\frac{1}{5}$ from $\frac{1}{4}$.

Step 1: Identify the LCM

Multiples of 4 = 4, 8, 12, 16, 20, 24 . . .

Multiples of 5 = 5, 10, 15, 20 . . .

So, the LCM here is 20.

Step 2: Convert each fraction to a fraction with the least common denominator.

$\frac{1}{4} = \frac{1}{4}  \times \frac{5}{5} = \frac{5}{20}$

$\frac{1}{5} = \frac{1}{5}  \times \frac{4}{4} = \frac{4}{20}$

Step 3: Subtract the fractions and simplify.

$\frac{1}{4}$ $–$ $\frac{1}{5}$

$= \frac{5}{20}$ $–$ $\frac{4}{20}$

$= \frac{5 – 4}{20}$

$= \frac{1}{20}$

Solved Examples on Unit Fraction

Example 1: Find the sum of $\frac{1}{3}$ and $\frac{1}{7}$.

Solution:

Step 1: Identify the least common multiple of the denominators.

Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24

Multiples of 7: 7, 14, 21

So, the LCM is 21.

Step 2: Convert each fraction to an equivalent fraction with the least common multiple as the denominator.

Now, we convert the fractions into a denominator with the LCM.

$\frac{1}{3} = \frac{1}{3}  \times \frac{7}{7} = \frac{7}{21}$

$\frac{1}{7} = \frac{1}{7}  \times \frac{3}{3} = \frac{3}{21}$

So,

$\frac{1}{3} + \frac{1}{7}$

$= \frac{7}{21} + \frac{3}{21}$

$= \frac{7 + 3}{21}$

$= \frac{10}{21}$

Example 2.  Subtract $\frac{1}{8}$ from $\frac{1}{6}$.

Solution:

Multiples of 8: 8, 16, 24, 32

Multiples of 6: 6, 12, 18, 24, 

So, the LCM is 24.

Now, we convert the fractions into a denominator with the LCM.

$\frac{1}{8} = \frac{1}{8}  \times \frac{3}{3} = \frac{3}{24}$

$\frac{1}{6} = \frac{1}{6}  \times \frac{4}{4} = \frac{4}{24}$

So,

$\frac{1}{6}$ $–$ $\frac{1}{8}$

$= \frac{4}{24}$ $–$ $\frac{3}{24}$

$= \frac{4–3}{24}$

$= \frac{1}{24}$

Practice Problems on Unit Fraction

Frequently Asked Questions on Unit Fraction