A multiple is the product result of one number multiplied by another number.
For example, we can get the multiples of 5 by multiplying 5 with numbers 1, 2, 3, and so on.
Multiples of 5 are: 5, 10, 15, 20, 25…
If a number is a multiple of two or more numbers, it is called a common multiple. For example, 2 x 5 = 10.
Therefore, 10 is a multiple of both 2 and 5. Thus, 10 is said to be a common multiple of both 2 and 5.
What Is Least Common Multiple (LCM)?
LCM is the short form for “Least Common Multiple.” The least common multiple is defined as the smallest multiple that two or more numbers have in common.
For example: Take two integers, 2 and 3.
Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20….
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 ….
6, 12, and 18 are common multiples of 2 and 3. The number 6 is the smallest. Therefore, 6 is the least common multiple of 2 and 3.
So, what is LCM in math? The LCM of two numbers is the smallest number divisible by both numbers.
One prime application of LCM is finding the lowest common denominator (LCD) of two or more fractions. It plays a significant role in adding, subtracting, and comparing two or more fractions.
Recommended Games
How to Find Least Common Multiple (LCM)?
Different methods to determine the LCM of a set of numbers are:
- Listing the multiples
- Prime Factorization
- Division Method
Recommended Worksheets
Listing the Multiples Method
To find the LCM using multiples, list the multiples of the numbers in the table as shown. The least common multiple is the first common multiple for the given numbers.

For 12 and 16, the number 48 is the LCM.
Prime Factorization Method
The prime factorization method involves finding the prime factors of the given numbers and identifying the least common multiple (LCM). For example, pair the common multiples shown to find the least common multiple of 12 and 16 using the prime factorization. List them along with the remaining multiples.
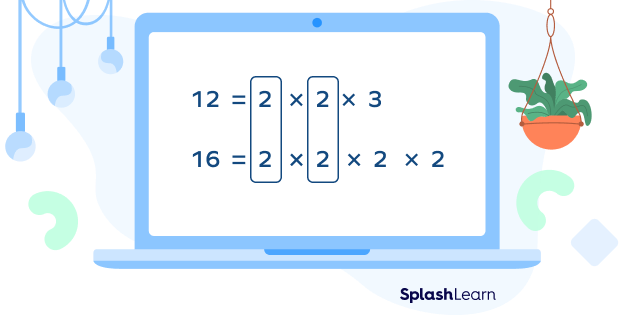
LCM = 2 × 2 × 2 × 2 × 3 = 48
Division Method
In this method, the given numbers are divided by the common divisors until there is no possible further division by the same number. The divisors and the remainders are multiplied to obtain the least common multiple.
For example,
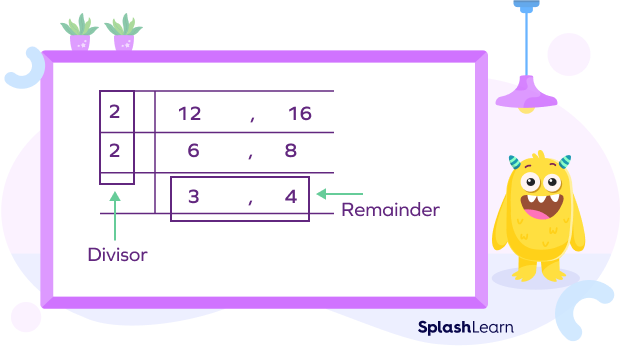
LCM = 2 × 2 × 3 × 4 = 48
Relation Between LCM and HCF
The highest common factor of two or more numbers is the HCF of the given numbers. The smallest number among all common multiples of the given numbers is the least common multiple of two or more numbers. Assuming a and b are two numbers, the formula for determining the relationship between their LCM and HCF is:
LCM (a, b) × HCF (a, b) = a × b
Solved Examples On Least Common Multiple
Example 1: Find the LCM of 18 and 24 using the prime factorization method.
Solution:
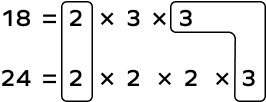
LCM = 2 × 2 × 2 × 3 × 3 = 72
Example 2: Find the smallest number divisible by 9 and 15.
Solution:
The smallest number divisible by 9 and 15 is the LCM of 9 and 15.
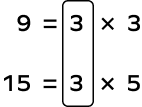
LCM = 3 × 3 × 5 = 45
So, 45 is the smallest number divisible by both 9 and 15.
Example 3: The product of the two numbers is 180. If their HCF is 3, what is their LCM?
Solution:
The highest common factor (HCF) is 3, and the product of the numbers is 180.
Since, LCM × HCF = product of numbers, LCM = 1803 = 60
Therefore, the LCM is 60.
Practice Problems On Least Common Multiple
Least Common Multiple - Definition With Examples
The LCM of the two numbers is 12. Which of the following could be the other number if one of the numbers is 3?
The LCM of a number and any of its multiples is the multiple itself.
The LCM of two prime numbers is 91. What could the other number be if one of the numbers is 7?
The LCM of two prime numbers is the product of the numbers. Since 7a = 91, a = 91/7 = 13
The HCF of two numbers, A and B, is 1. Which of the following is the LCM of A and B?
LCM × HCF = product of numbers
Which of the following is the LCM of 20 and 60?
LCM of 20 and 60 = 60
Frequently Asked Questions On Least Common Multiple
How are the HCF and LCM of the two numbers related?
The product of LCM and HCF of any given two numbers is equal to the product of those two numbers.
What is the difference between LCM and HCF?
The LCM (Lowest Common Multiple) of two or more numbers is the smallest number among all common multiples of the provided numbers. In contrast, the HCF (Highest Common Factor) is the highest number among all the common factors of the given numbers.
Why is the LCM of two co-prime numbers always their product?
The only common factor between the two co-prime numbers is 1. So, the HCF of two coprime numbers is always 1. If a and b are two co-prime numbers, then by the relationship between LCM and HCF, we get
LCM (a, b) × HCF (a, b) = a × b
Since a and b are co-prime numbers, their HCF is always 1. So, we get that the LCM of a and b is always the product of a and b.




































