Converting Fractions into Decimals – Methods, Facts, Examples

What Is Fractions-to-Decimals Conversion?

Converting a fraction into its equivalent decimal form is known as fraction-to-decimal conversion. Converting fractions to decimals allows for more accurate and precise mathematical calculations. 

Fraction to a decimal formula is given as a ÷ b, where a is the numerator and b is the denominator of the fraction. In simple words, to turn fractions into decimals, we simply divide the numerator by the denominator.

In this conversion, you express a fraction as a decimal number with a whole number part and a decimal part.

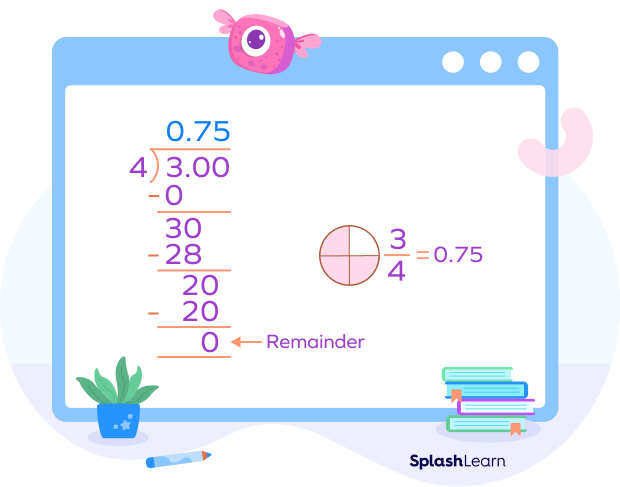
Example: When you convert the fraction $\frac{3}{4}$ to a decimal, you get 0.75. Here, 0 is the whole number part, and 0.75 is the decimal part.

How to Convert Fractions into Decimals

There’s no specific fraction-to-decimal formula for conversion. Let’s learn two ways to turn fractions into decimals:

1. Long division method

2. By converting the denominator of the fraction into a power of 10

How to Convert Fractions into Decimals Using the Long Division Method

In this method, we treat the numerator as a dividend and the denominator as the divisor. We carry out the long division till we get 0 as the remainder or at least three decimal places in the quotient. Using the long division method, let’s take examples to understand how to convert a fraction into a decimal. 

Example 1: Find the decimal form of the fraction $\frac{7}{5}$ using the long division method.

Example 2: Find the decimal form of the fraction $\frac{3}{5}$ using the long division method.

Example 3: Convert $\frac{2}{11}$ into a decimal.

How to Convert Fractions into Decimals by Changing the Denominator into a Power of 10

In this method, we multiply both the numerator and denominator by an appropriate number such that the denominator changes into a power of 10. Simply put, we try to convert the fraction into a decimal fraction. A fraction whose denominator is a power of 10 can be easily converted into a decimal by simply moving the decimal point.

Note: 

• When we multiply both the numerator and denominator by the same number, we are not changing the value of the fraction. We are just finding the equivalent fraction with the denominator as a power of 10.
• This method is perfect for fractions whose denominator can be changed into a power of 10. For fractions like $\frac{3}{7}$ or  $\frac{1}{3}$, this method is not suitable.

Example 1: Convert $\frac{4}{5}$ into a decimal.

Numerator $= 4$

Denominator $= 5$

Think of a number by which we can multiply 5 to turn it into a power of 10.

5 times 2 is 10.

$5 \times 2 = 10$

Thus, multiply the numerator and denominator by 2.

$\frac{4}{5} = \frac{4 \times 2}{5 \times 2} = \frac{8}{10} = 0.8$

Example 2: Find the decimal form of the fraction $\frac{3}{8}$.

Numerator $= 3$

Denominator $= 8$

We know that $8 \times 125 = 1000$

Thus, multiply the numerator and denominator by 125.

$\frac{3}{8} = \frac{3 \times 125}{8 \times 125} = \frac{375}{1000} = 0.375$

Fraction-to-Decimal Chart

The Fraction to Decimal chart simplifies the conversion by displaying common fractions and their decimal equivalents.

• In proper fractions, the numerator is less than the denominator. Thus, the resulting decimals are also less than 1.
• In improper fractions, the numerator is greater than or equal to the denominator. Thus, the resulting decimals are greater than or equal to 1.

Let’s convert some common fractions to decimals and list them in a chart.

Fraction	Decimal
$\frac{1}{2}$	0.5
$\frac{1}{3}$	$0.\overline{3} = 0.333$…
$\frac{1}{4}$	0.25
$\frac{1}{5}$	0.2
$\frac{1}{6}$	0.16
$\frac{1}{8}$	0.125
$\frac{1}{10}$	0.1
$\frac{1}{100}$	0.01
$\frac{3}{7}$	$0.\overline{428571}$
$\frac{3}{2}$	1.5
$\frac{3}{4}$	0.75
$\frac{4}{3}$	1.33…

When Do Fractions Turn into Terminating and Repeating Decimals?

• If the denominator of the fraction in its lowest form has the prime factorization consisting only of 2s and/or 5s, then the fraction results in a terminating decimal. 

Example: $\frac{7}{16}$

The fraction is already in its lowest form.

Denominator $= 16 = 2 \times 2 \times 2 \times 2$

The prime factorization of the denominator only contains 2s.

$\frac{7}{16} = \frac{7 \times 625}{16 \times 625} = \frac{4375}{10,000} = 0.4375$ …terminating decimal

• If the denominator of the fraction in its lowest form has the prime factorization consisting of factors other than 2s and 5s, then the fraction results in a repeating decimal. 

Example: $\frac{10}{24}$

$\frac{10}{24}$ in lowest form $= \frac{5}{12}$

Denominator $= 12 = 2 \times 2 \times 3$

The prime factorization of the denominator has 2s and 3s.

$\frac{10}{24} = \frac{5}{12} = 0.416$ …repeating decimal

Alt tag: Converting 5/12 into a decimal

Facts about Converting Fractions into Decimals

Conclusion

In this article, we learned about the fraction-to-decimal conversion with two methods and several examples. Let’s take a look at a few more solved examples and practice problems for better comprehension.

Solved Examples on Converting Fractions into Decimals

Example 1: Convert $\frac{2}{5}$ into decimal form using the long division method.

$\frac{2}{5}$

Solution:

To convert $\frac{2}{5}$ to a decimal, divide the numerator 2 by the denominator 5. 

$\frac{2}{5} = 0.4$

Example 2: Find the decimal form of $\frac{9}{25}$.

Solution:

Numerator $= 9$

Denominator $= 25$

We know that “25 times 4 is 100.”

Thus, multiply both the numerator and the denominator by 4.

$\frac{9}{25} = \frac{9 \times 4}{25 \times 4 = \frac{36}{100} = 0.36$ 

Thus, $\frac{9}{25} = 0.36$

Example 3. Compare $\frac{11}{20}$ and 0.5.

Solution:

Let’s convert $\frac{11}{20}$ into a decimal form to compare it with 0.5 easily.

To convert $\frac{11}{20}$ to a decimal, multiply both the numerator and the denominator by 5.

$\frac{11}{20} = \frac{11 \times 5}{20 \times 5} = \frac{55}{100} = 0.55$

We know that 0.5 < 0.55

Thus, 0.5 < 1120.

Practice Problems on Converting Fractions into Decimals

Frequently Asked Questions about Converting Fractions into Decimals