What Is a 270 Degree Angle?
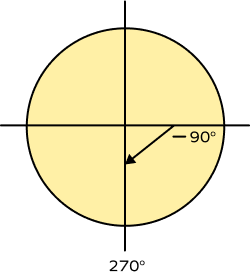
A 270-degree angle is a reflex angle. It spans three-quarters of a full rotation or a circle. In radians, a 270-degree angle is equivalent to $\frac{\pi3}{2}$ radians.
It is larger than a straight angle (180 degrees) but smaller than a complete angle (360 degrees).
In geometric terms, a full circle is divided into 360 degrees. So, a 270-degree angle is just 90 degrees short of a complete revolution.
So, what does a 270-degree angle look like?
A 270-degree angle is equivalent to $\frac{3}{4}$th of a full turn. To visualize a 270-degree angle, imagine starting from a reference point and rotating in a counterclockwise direction until you cover three 90-degree angles.
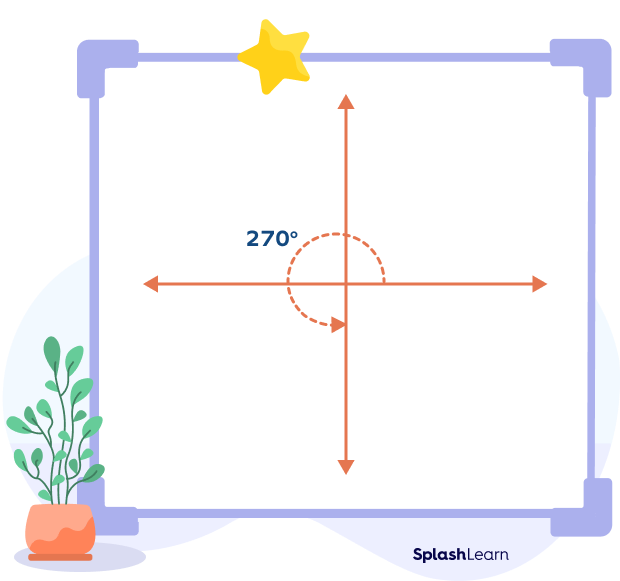
An angle is a geometric figure formed by two rays sharing a common endpoint called the vertex. The two rays are called the arms or sides of the angle. The size of an angle is measured in degrees (represented by the symbol °) or radians (abbreviated as rad).
There are various types of angles, like acute angle, obtuse angle, and right angle, based on the angle measure. Today, we will talk about the angle that measures 270 degrees.
Recommended Games
How to Construct a 270-Degree Angle
Let’s discuss two methods to construct a 270-degree angle.
- Method 1: Construction of a 270-degree Angle with a Compass and Ruler
We know that $270^{\circ} = 360^{\circ} – 90^{\circ}$ is a corresponding reflex angle of a right angle.
To construct a 270-degree angle, we will first construct a 90-degree angle using a compass and ruler. The corresponding reflex angle will be the 270-degree angle.
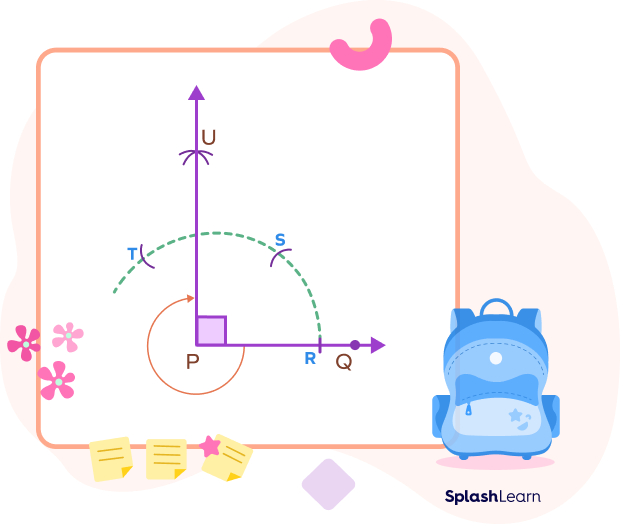
Step 1: Using a ruler, draw ray PQ.
Step 2: Place the compass point at P, draw an arc intersecting line PQ, and mark the intersection as R.
Step 3: Place the compass point at R, draw an arc intersecting the previous arc with radius PR, and label the intersection point as S.
Step 4: Using the compass at point S, intersect the initial arc created in Step 2 with another arc of radius PR. Mark the intersection point as T.
Step 5: Using the compass at point S, draw an arc with radius PR between points S and T.
Step 6: Using the compass at point T, draw an arc with the same radius PR to intersect the arc drawn in step 5. Mark the point of intersection as U.
Step 7: Join U and P.
m∠UPQ = 90°
The reflex angle corresponding to the ∠UPQ is 360° – 90° = 270°.
- Method 2: Construction of a 270-degree Angle with a Protractor
Constructing a 270-degree angle using a protractor can be done by adding a 180-degree angle and a 90-degree angle together. Follow the following steps to construct a 270-degree angle with the protractor:
- Align the protractor’s center with the reference line and draw the line segment (reference line).
- From the $0-^{\circ}$ line, count anticlockwise to $180-^{\circ}$. Then, continue another $90-^{\circ}$ from the $180-^{\circ}$ mark.
- Mark this endpoint and connect it with the center point. This forms the $270-^{\circ}$ angle when measured in the anticlockwise direction.
Another simple way to draw a 270-degree angle is to use the full-circle protractor and mark the point representing the 270 degrees.
Recommended Worksheets
270 Degree Angle in Terms of Pi
To express a 270-degree angle in terms of pi ($\pi$), we need to convert it into radians.
Angle in radians = Angle in degrees $\times (\frac{\pi}{180})$
270 degrees $\times (\frac{\pi}{180}) = (\frac{\pi3}{2})$ radians.
Therefore, a 270-degree angle can be represented as $(\frac{\pi3}{2})$ radians.
Also, $1^{\circ} = (\frac{\pi}{180})$ radians $= 0.017453$ radians.
Therefore, $270^{\circ} = 270^{\circ} \times 0.017453 =$ 4.71239 radians.
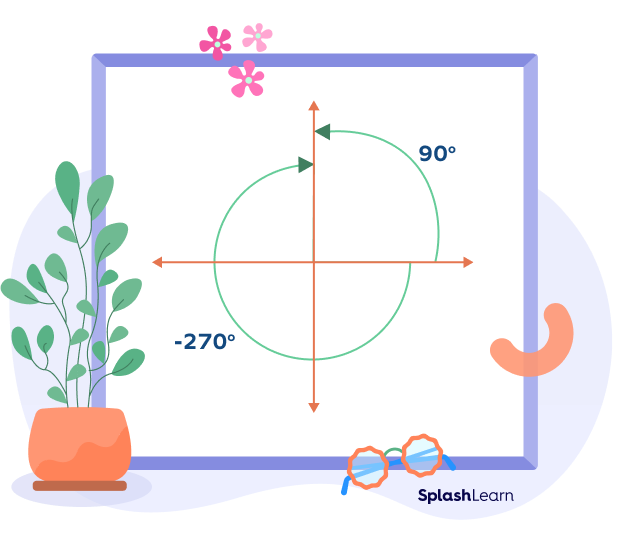
Negative 270-Degree Angle
A negative angle is generated by rotating the terminal arm clockwise by 270 degrees.
Facts about 270 Degree Angle
- A 270-degree angle spans three-quarters of a full circle. It is larger than a straight angle (180 degrees) but smaller than a full revolution (360 degrees).
- A 270-degree angle is classified as a reflex angle. Reflex angles are angles greater than 180 degrees but less than 360 degrees. They “bend back” beyond a straight angle.
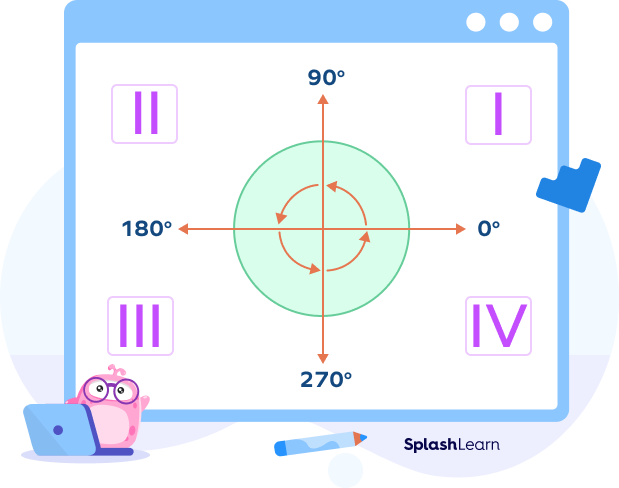
- In a Cartesian coordinate system, a 270-degree angle lies in the third quadrant, where both the x-coordinate and y-coordinate are negative.
- A 270-degree angle is three times the right angle.
- Combining three right angles means the total angle measure is 270 degrees.
- A 270-degree angle is three-quarters of a complete angle.
Conclusion
In this article, we have learned about a 270-degree angle. Understanding a 270-degree angle and angles in general allows you to approach and solve problems effectively, whether they involve spatial reasoning, measurements, or calculations. Let’s solve some examples and practice problems to understand the concept better.
Solved Examples on 270 Degree Angle
Example 1: Anna divided a pizza into four equal pieces and picked up one slice to eat. What are the angles formed at the center of the pizza?
Solution:
A whole pizza represents a full circle (360 degrees).
Anna divided it into four quarters and picked up one slice. Now, the pizza looks like this:

Thus, two angles are formed: one right angle and its corresponding reflex angle, which is a 270-degree angle.
The original corner of the square forms a right angle (90 degrees) with the center. When rotated by 270 degrees, the corner will be in the opposite direction, forming a straight line with the center. Thus, the angle formed will be 180 degrees.
Example 2: An angle measures 270 degrees. What is the reference angle?
Solution:
The reference angle is the acute angle formed between the terminal side of the angle and the x-axis.
In this case, the reference angle would be 90 degrees since it is the difference between 270 degrees and one full revolution (360 degrees).
Example 3: Mona started studying at 09:00 a.m. and finished at 09:45 a.m. What is the angle covered by the minute hand?
Solution:
Starting time = 09:00
Ending time = 09:45
Total time = 45 minutes
A minute hand covers a 6-degree angle in 1 minute. So, in 45 minutes, it will cover $45 \times 6 = 270$ degrees.

The angle made by the hands of the clock is 270 degrees in the clockwise direction.
Practice Problems on 270 Degree Angle
270 Degree Angle - Construction, in Radians, Examples, FAQs
Which of the following statements about a 270-degree angle is true?
A reflex angle is an angle that measures greater than 180 degrees but less than 360 degrees. A 270-degree angle falls within this range, making it a reflex angle.
How many radians are 270°?
To convert degrees into radians, we multiply the degree measure by $(\frac{\pi}{180})$. Therefore, 270 degrees$\times \frac{\pi}{180} = \frac{3\pi}{2}$ radians.
How many right angles make a 270-degree angle?
A right angle measures 90 degrees, so a 270-degree angle consists of three right angles.
$3 \times 90$ degrees$ = 270$ degrees
When do clock hands make a 270-degree angle in an analog clock?
At 9 o’clock, the hands of the clock make a 270-degree angle.
Frequently Asked Questions on 270 Degree Angle
Is a 270° angle a straight angle?
No, a 270° angle is not a straight angle. A straight angle measures exactly 180 degrees, while a 270-degree angle is greater than that. A 270-degree angle is a reflex angle, as mentioned earlier, which is an angle greater than 180 degrees but less than 360 degrees.
How do you convert 270 degrees into radians?
To convert 270 degrees to radians, you can use the following formula:
Radians = Degrees $\times (\frac{\pi}{180})$.
Therefore, 270 degrees $= 270^{\circ} (\frac{\pi}{180}) = (\frac{\pi3}{2})$ radians.
What is the difference between a 270-degree angle and a straight angle?
A straight angle measures exactly 180 degrees, while a 270-degree angle is larger than that. A 270-degree angle is a reflex angle, whereas a straight angle is not.
Is a 270-degree angle obtuse?
No, a 270-degree angle is not an obtuse angle. It is a reflex angle.





























