Types of Angles – Definition with Examples

What Are Types of Angles?

We study types of angles based on –

• measurement 
• rotation 

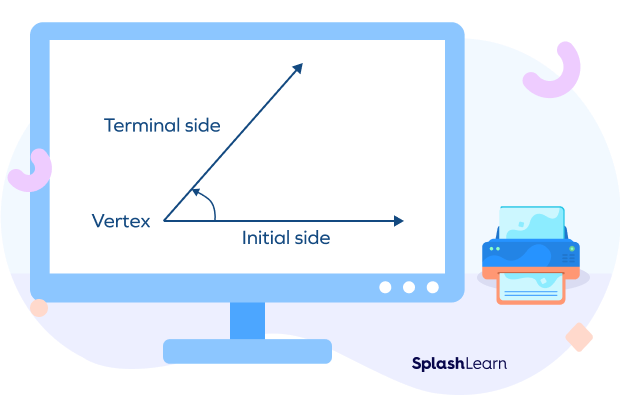
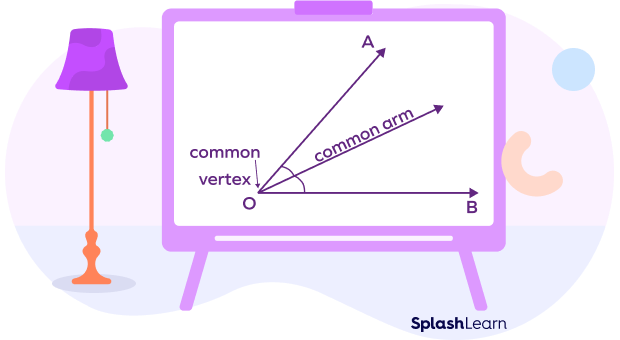
An angle is formed when two rays or straight lines meet at a common endpoint called vertex. The rays that form a vertex are also called arms or sides.

How to Name an Angle

To denote an angle, we use the symbol ∠.

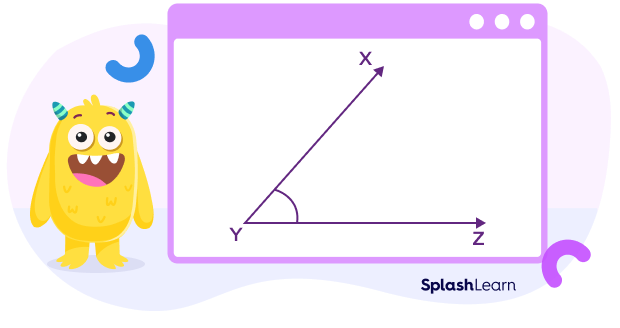
We can name the angles in two ways. Observe the diagram given below.

• The vertex is Y. So, we can name the angles as ∠Y. 
• To name an angle, you can also use three points, the vertex, and any two points on its arms as ∠XYZ or ∠ZYX.

How to Measure an Angle

To measure an angle, you can follow these concise bullet points:

• Place the vertex of the angle at the center of a protractor.
• Align one of the angle’s rays with the baseline of the protractor.
• Read the angle measurement where the other ray intersects the protractor scale.
• Ensure the protractor’s zero mark aligns with one ray for accurate measurement.

A protractor can be used to construct and measure the angle.

Suppose we have to measure the angle given below. 

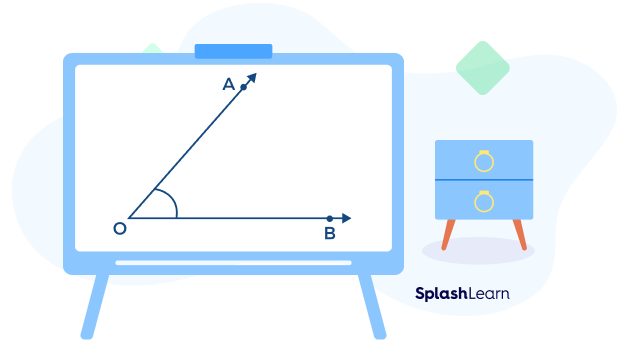
The steps to measure an angle are: 

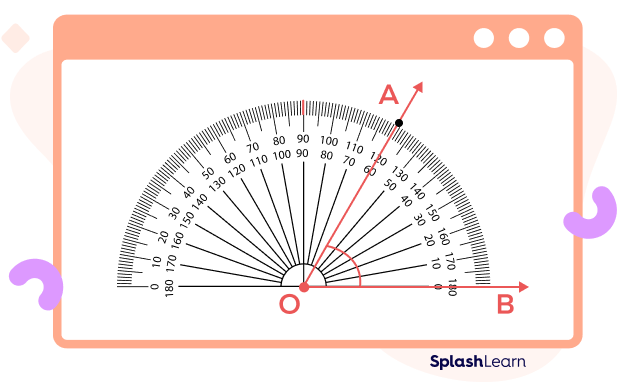
• Align the protractor with the ray OB. Start reading from the 0° and mark on the bottom-right of the protractor as shown below. 
• The number that coincides with the second ray on the protractor is the measure of the angle. 

In this case, the second ray coincides with 60°. So, we can write m∠AOB = 60°.

Types of Angles Based on Measurement

There are 5 types of angles based on measurement:

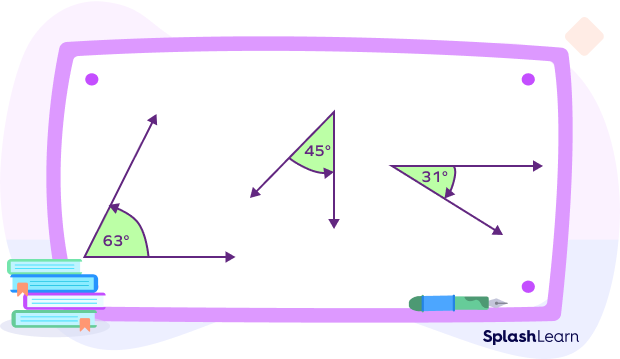
• Acute Angle

An acute angle is an angle that lies between 0° and 90°. 

Examples: 35°, 80°, 72° etc. 

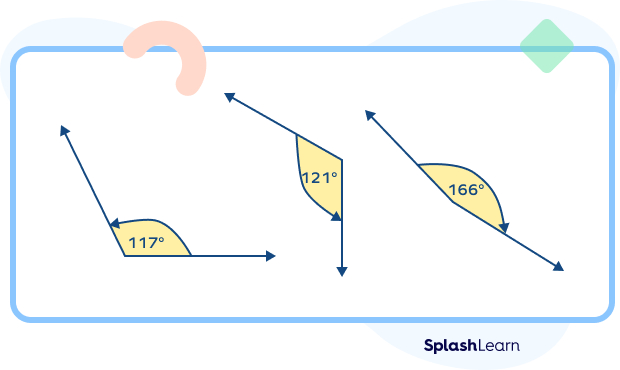
• Obtuse Angle

An obtuse angle is an angle which lies between 90° and 180°. 

Examples: 135°, 150°, 122°, etc. 

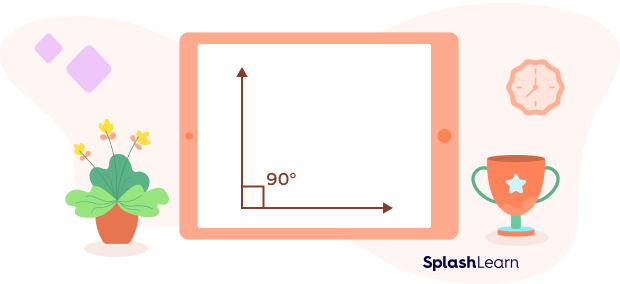
• Right Angle

A right angle is an angle that precisely measures 90 degrees.

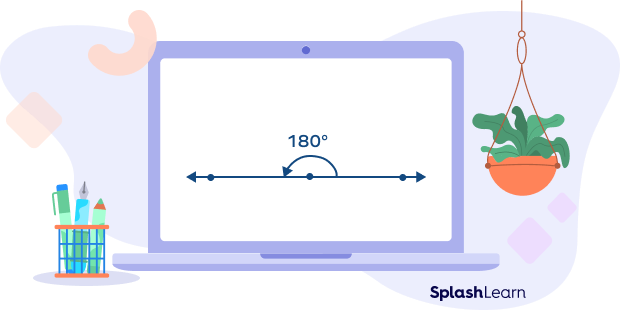
• Straight Angle

A straight angle is an angle that precisely measures 180°. It looks like a straight line.

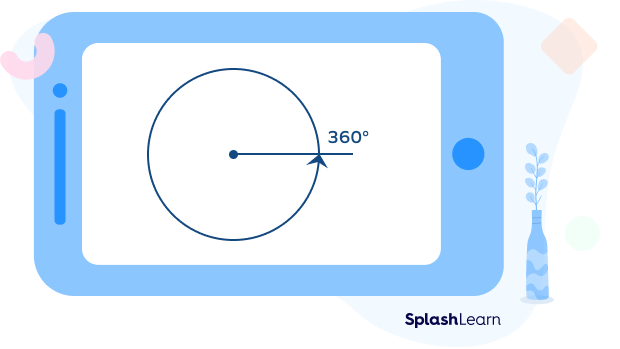
• Complete Angle

An angle equal to 360º is called full rotation or complete angle. It is formed when one of the arms takes a full or complete rotation to form an angle. 

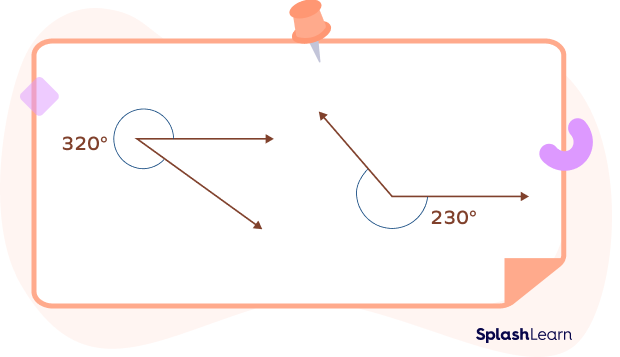
• Reflex Angle

The angles between a straight angle (180º) and a full turn (360º) are called reflex angles.

Types of Angles Based on Direction of Rotation

There are 2 types of angles based on the direction in which a ray rotates to form an angle. 

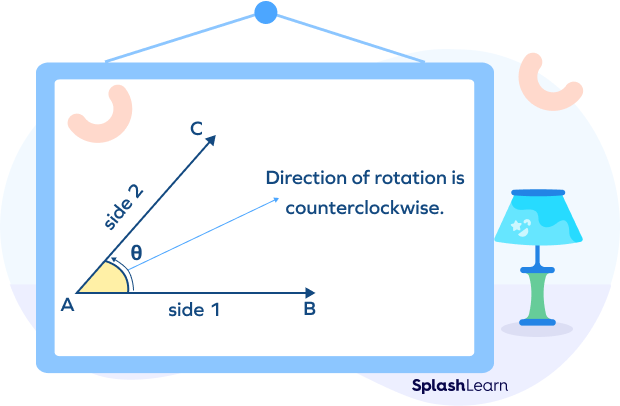
• Positive Angle

Positive angles are the angles that are formed when the initial ray is rotated from the base in the counterclockwise direction. 

In the figure given below, AB is rotated in the counterclockwise direction by an angle θ. Thus, a positive angle is formed.

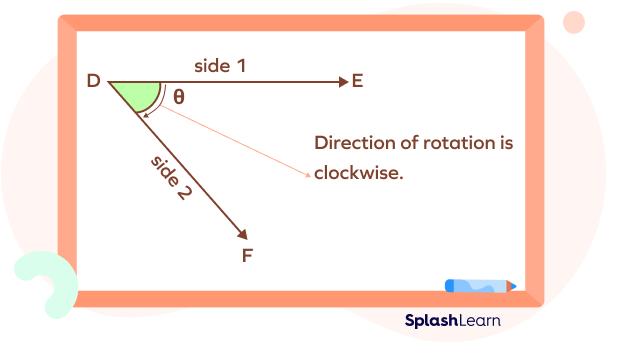
• Negative Angle

Negative angles are the angles that are formed when the initial ray is rotated in the clockwise direction. 

In the figure given below, the ray DE is rotated in the clockwise direction by an angle θ. Thus, a negative angle is formed.

Angle Pairs

Two angles together form an angle pair. Let’s learn about some important types of angle-pairs.

• Complementary Angles

Two angles are considered complementary if the sum of two angles is equal to 90°. In other words, we can say that one angle is a complement of another angle. Note that two angles need not be adjacent to be complementary. 

Example 1: Angles measuring 20° and 70° are complementary angles since their sum is 90°. 

Example 2: The complement of 40° is (90° – 40°) = 50°.

• Supplementary Angles

Two angles are considered supplementary if they add up to 180°. 

Example 1: 120° + 60° = 180°. 

Thus, the two angles are supplementary. 

Example 2: The supplementary angle of 30° is (180° – 30°) = 150°.

• Adjacent Angles

Two angles are said to be adjacent angles if they satisfy the following conditions:

• Two angles share a common vertex.
• Two angles share one common arm.
• They do not overlap

 In the figure given below, ∠AOC and ∠BOC are adjacent angles. 

• Vertically Opposite Angles

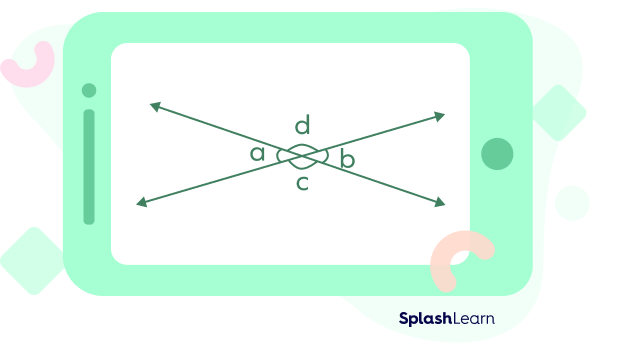
Vertically opposite angles are formed when two lines intersect each other. These angles are opposite to each other and are always congruent. They only share a common vertex.

In the figure, vertically opposite angles are

• ∠a and ∠b (∠a = ∠b)
• ∠b and ∠d (∠b = ∠d)

• Linear Pair of Angles

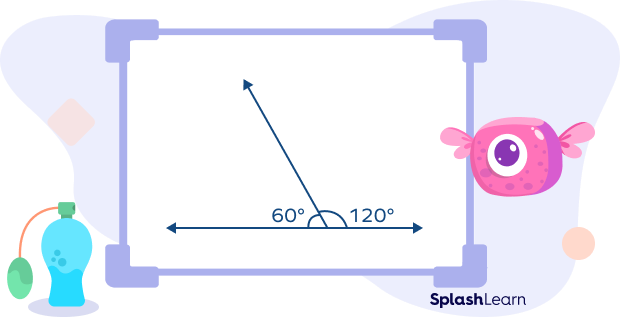
A linear pair of angles is formed when two adjacent angles share a common vertex and combine to form a straight line, resulting in a sum of 180 degrees.

For example, in the given diagram the angles 60° and 120° form angles in a linear pair.

60° + 120° = 180°

Angles Formed by Two Parallel Lines and a Transversal

When two parallel lines are intersected by a third line (transversal), a variety of angles are formed. These angles possess unique properties and relationships, providing valuable insights into geometric configurations. Understanding these angle types is essential for solving geometric problems and proofs.

Note that these angles are also formed when two non-parallel lines are cut by a transversal. However, in case of non-parallel lines, the angles do not possess any special properties.

Angle Names	Image	Description
Corresponding Angles		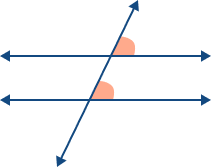Angles on the same side of the transversal and on the same side of the parallel lines, in corresponding positions. They are always equal.
Alternate Interior Angles		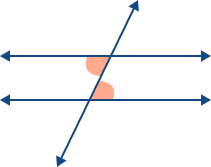Angles on opposite sides of the transversal, inside the parallel lines. They are always equal.
Alternate Exterior Angles		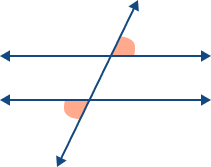Angles on opposite sides of the transversal, outside the parallel lines. They are always equal.
Interior Angles on the Same Side (Same Side Interior Angles)		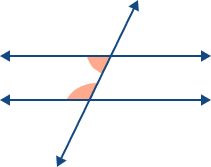Angles on the same side of the transversal, inside the parallel lines. They are supplementary.
Exterior Angles on the Same Side (Same Side Exterior Angles)		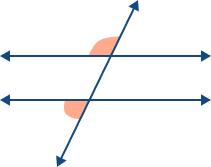Angles on the same side of the transversal, outside the parallel lines. They are always supplementary.

Facts about Types of Angles

Solved Examples on Types of Angles

1. Classify given angles as acute, obtuse, right, reflex, or straight.

i) 32.5°

ii) 90°

iii) 359°

iv) 180°

v) 90.05°

Solution: 

i) 32.5° – acute angle

ii) 90° – right angle

iii) 359° – reflex angle

iv) 180° – straight angle

v) 90.05° – obtuse angle

2. Are supplementary angles always adjacent?

Solution: 

Supplementary angles need not be adjacent. Supplementary angles may or may not be adjacent.

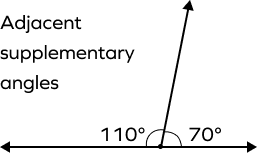
Example 1: Adjacent supplementary angles

110° + 70° = 180°

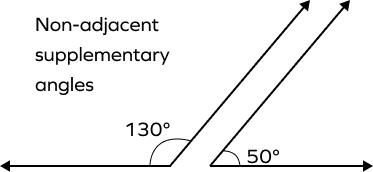
Example 2: Supplementary angles that are not adjacent:

130° + 50° = 180°

3. Name 4 pairs of adjacent angles in the following figure.

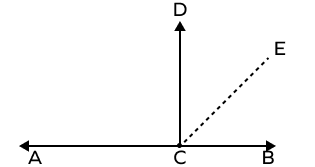
Solution:  

Adjacent angles always share a common vertex and a common arm.

(a) ∠ACD and ∠DCE

(b) ∠ACD and ∠DCB

(c) ∠DCE and ∠ECB

(d) ∠ECB and ∠ACE

There are 4 pairs of adjacent angles. 

Practice Problems on Types of Angles

Frequently Asked Questions on Types of Angles