What is Place Value?
In math, every digit in a number has a place value. Place value can be defined as the value represented by a digit in a number on the basis of its position in the number.
For example, the place value of 7 in 3,743 is 7 hundreds or 700. However, the place value of 7 in 7,432 is 7 thousands or 7,000. Here, we can see that even though the digits are same in both the numbers, it’s place value changes with the change in it’s position.
Place Value Chart
Place Value Chart is a very useful table format that helps us in finding the place value of each digit based on it’s position in a number.
The place value of a digit increases by ten times as we move left on the place value chart and decreases by ten times as we move right.
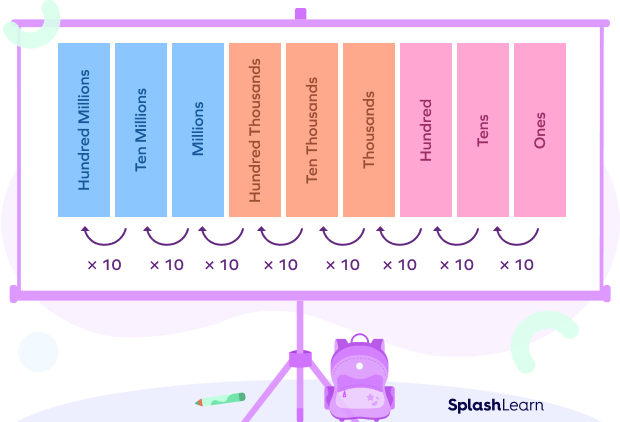
Here’s an example of how drawing the place value chart can help in finding the place value of a number.
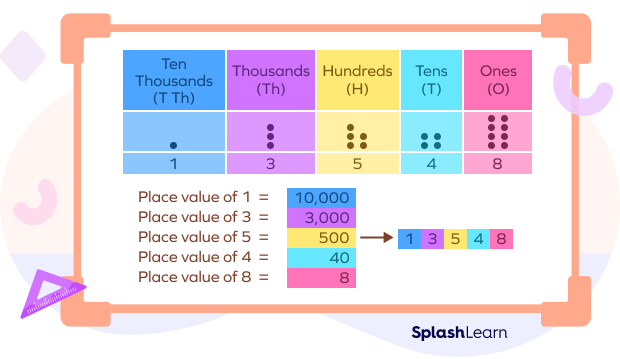
In the number 13,548
1 is in the ten thousands place and has a place value of 10,000.
3 is in the thousands place and has a place value of 3,000.
5 is in the hundreds and has a place value of 500.
4 is in the tens place and has a place value of 40.
8 is in the ones place and has a place value of 8.
Understanding the place value of digits in numbers helps comparing numbers. It also helps in writing numbers in their expanded form. For instance, the expanded form of the number above, 13,548 is 10,000 + 3,000 + 500 + 40 + 8.
Place Value Using Base Ten Blocks
The place value of digits in numbers can also be represented using base-ten blocks and can help us write numbers in their expanded form.
Before, using the base ten blocks to find the place value of each digit in a number, let us first understand what these blocks represent.
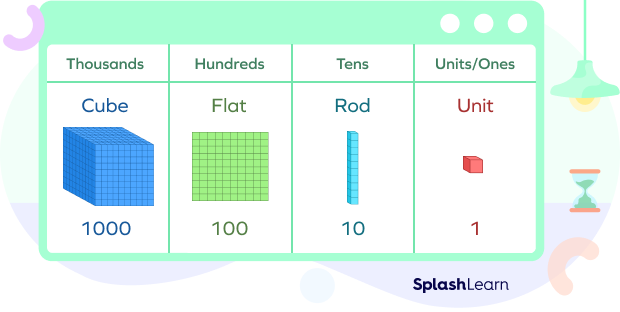
Here’s how the number 13,548 can be represented using base-ten blocks.
Decimal Place Value
Decimal numbers are fractions or mixed numbers with denominators of powers of ten. In a decimal number, the digits to the left of the decimal point represent a whole number. The digits to the right of the decimal represent the parts. As we move towards right after the decimal point, the place value of the digits becomes 10 times smaller.
The first digit on the right of the decimal point means tenths i.e. 110. The next place becomes ten times smaller and is called the hunderdths i.e. 1100 and so on.
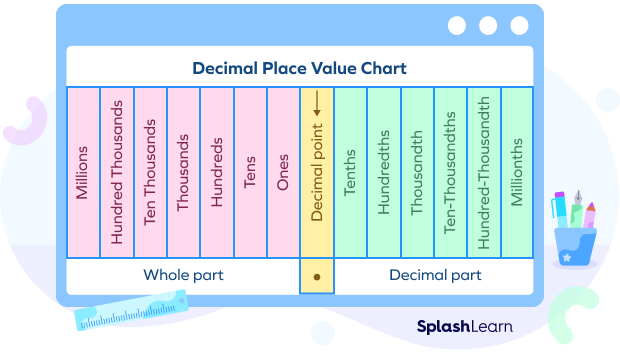
In 27.356, 27 is the whole number part, 2 is in tens place and its place value is 20,7 is in ones place, and its place value is 7.
There are three digits to the right of the decimal point,
3 is in the tenths place, and its place value is 0.3 or 310
5 is in the hundredths place, and its place value is 0.05 or 5100
6 is in the thousandths place, and its place value is 0.006 or 61000
Place Value and Face Value
Place value and face value are not the same. The face value of a digit is the value of the digit whereas the place value of a digit is it’s place in the number. In simple words, the face value tells the actual value of the digit whereas the place value tells the value of the digit, based on it’s position.
Hence, the face value of the digit never changes irrespective of it’s position in the number. Whereas, the place value of the digit changes with the change in the position.
For instance, the face value of 2 in both the numbers 283 and 823 is 2. Whereas, the place value of 2 is 200 in 283 and 20 in 823.
Solved Examples
- What is the place value of 4 in the number 84,527?
Solution:
The place value of 4 in 84,527 is 4000 (four thousand).
- Write 412,397 in words using the place value system.
Solution:
Four hundred twelve thousand three hundred and ninety-seven.
- Write the numbers in figures and in expanded form:
- Ten thousand two hundred and thirty-six
- Seven thousand four hundred and eighty-five
Solution:
- Ten thousand two hundred and thirty-six = 10,236
= 10,000 + 200 + 30 + 6
- Seven thousand four hundred and eighty-five = 7,485
= 7,000 + 400 + 80 + 5
Practice Problems
Place Value1Which digit is at the ten thousands place in the number 783,425?7 4 8 5 CorrectIncorrect Correct answer is: 8 8 is in the ten - thousands place. 2Select the correct answer in standard form. |
Frequently Asked Questions
Why is understanding place value important?
Place value has its application in many mathematical concepts. It builds the foundation for regrouping, multiplication, etc.
What manipulatives are used to teach place value?
Manipulatives such as base-10 blocks, snap cubes, unifix cubes, beans, etc., are used to develop place value understanding.
Does the place value of a digit increase as it moves from left to right?
No. The place value of a digit decreases by 10 times as it moves from left to right.
What is the difference between the face value and the place value of a digit?
The face value of a digit is the magnitude that it possesses naturally. It is independent of the digit’s position in the number. The place value of a digit depends on its position in the number. For example, the 5 in the number 253 has a face value of 5 and a place value is 50.