What Is an Expanded Form?
Expanded form is a way to express a number as the sum of the place values of its digits.
In the expanded form, we break up a number according to the place value of digits and expand it to show the value of each digit. For example, the expanded form of 943 is given below.
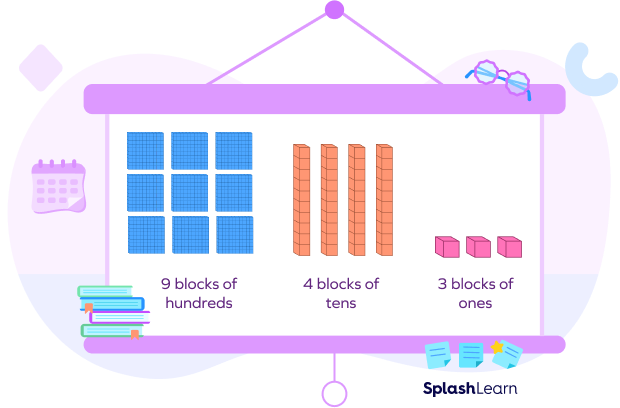
$943 = 9$ hundreds $+ 4$ tens $+ 3$ ones
Expanded Form: $943 = 900 + 40 + 3$
Recommended Games
Place Value
Recommended Worksheets
Place Value
Each digit in a number has a place value. It determines the value of that digit according to its position in the number. The value of a digit in a number increases as we move from left to right. The digits on the left have a lower place value than the digits on the right.
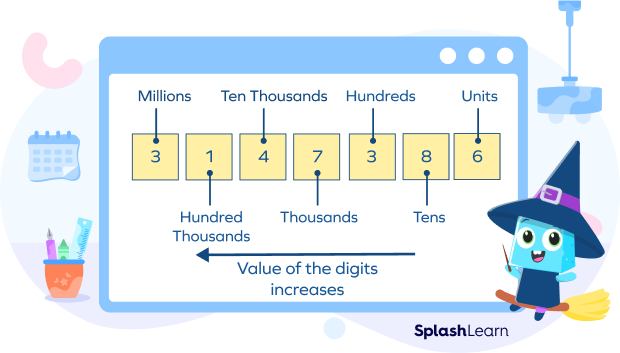
The value for each number is computed using the position of the number. Starting from right to left, we can understand the notations used in the place value using an example.
For the number 254, the place value chart is:

Thus, the expanded form of the number 254 is $200 + 50 + 4$.
Expanded Form Example
Let’s look at the number 875294831 as an example. This figure is tough to grasp. In this case, an expanded form assists us in understanding each of the numbers based on their place value.
875294831 can be written as $800000000 + 70000000 + 5000000 + 200000 + 90000 + 4000 + 800 + 30 + 1$
The number has been expanded to reflect the value of each of its digits.
How To Write Whole Numbers in Expanded Form
Here are the steps to write any whole number in expanded form.
- Get the number in its most basic form.
- Using the place value chart, determine its place values.
- Multiply the number by the number’s place value.
- Display it as a digit place value.
- All digits should be represented as the product of the digit and its place value.
Expanded Form with Decimals
The expanded form of a number with a decimal or a fraction is written with a base 10-multiple denominator, represented by the power of 10.
For example, the number 3.482 in expanded form is written as:
$3.482 = 3 + 0.4 + 0.08 + 0.002$
How To Write Decimals In an Expanded Form
First, consider the digit at ones place, which is 1.
$1 \times 1 = 1$
Next, we have the tenths place. The digit at the tenths place is 2.
We take 2 and multiply it by fraction $\frac{1}{10}$.
$1 + (2 \times \frac{1}{10})$
Then, we have the hundredth place. We move to a higher multiple of 10 for the denominator. In other words, we add another 0.
$1 + (2 \times \frac{1}{10}) + (3 \times \frac{1}{100})$
Finally, we have the thousandth place. Add another 0 in the denominator.
$1 + (2 \times \frac{1}{10}) + (3 \times \frac{1}{100}) + (4 \times \frac{1}{1000})$Hence, the expanded form of 1.234 is $1 + 0.2 + 0.03 + 0.004$.
Solved Examples On Expanded Form
- Write 589 in its expanded form.
Solution:
$589 = 5$ hundreds $+ 8$ tens $+ 9$ ones
$589 = 500 + 80 + 9$
The expanded form of 589 is $500 + 80 + 9$.
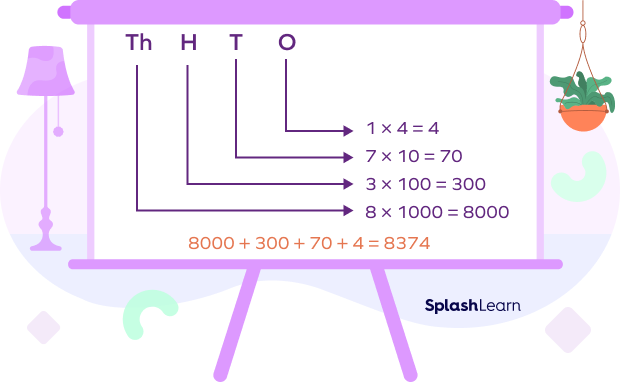
- Write 9677 in its expanded form.
Solution:
$9677 = 9$ thousands $+ 6$ hundreds $+ 7$ tens $+ 7$ ones
$9677 = 9000 + 600 + 70 + 7$
The expanded form of 9677 is $9000 + 600 + 70 + 7$.
- Write 23.782 in its expanded form.
Solution:
$23.782 = 2$ tens $+ 3$ ones $+ 7$ tenths $+ 8$ hundredths $+ 2$ thousandths
$23.782 = (2 \times 10) + (3 \times 1) + (7 \times \frac{1}{10}) + (8 \times \frac{1}{100}) + (2 \times \frac{1}{1000})$
$23.782 = 20 + 3 + 0.7 + 0.08 + 0.002$
The expanded form of 23 is $20 + 3 + 0.7 + 0.08 + 0.002$.
Practice Problems On Expanded Form
Expanded Form
Write 1080 in its expanded form.
The expanded form for $1080 = 1000 + 0 + 80 + 0$
Write 77 in its expanded form.
The expanded form for $77 = 70 + 7$
Write 567.25 in its expanded form.
The expanded form for $567 = 500 + 60 + 7 + 0.2 + 0.05$
Conclusion
In this article, we learnt about the expanded form of a number, place values, and how to write whole numbers and decimals in expanded form. Let’s solve a few examples and practice problems for better understanding.
Frequently Asked Questions On Expanded Form
What is the significance of expanded form?
Expanded form is important in math because it allows us to look at a number and identify the value of each digit.
What does writing in expanded form imply?
When we expand a number to illustrate each digit’s value, we write it in expanded form.. With extended form, we represent the numerical value of each digit in the number we’re writing. Except for zeroes, the larger the number is, the longer its expanded form will be when it is expanded.
Are expanded form and expanded notation the same?
No, expanded notation is recognized as a number that represents the sum of every digit in a particular number further multiplied by its respective place value.
Example of expanded form of 234 = 200 + 30 + 4 Example of expanded notation of 234 is 2 $\times$ 100 + 3 $\times$ 10 + 4 $\times$ 1




































