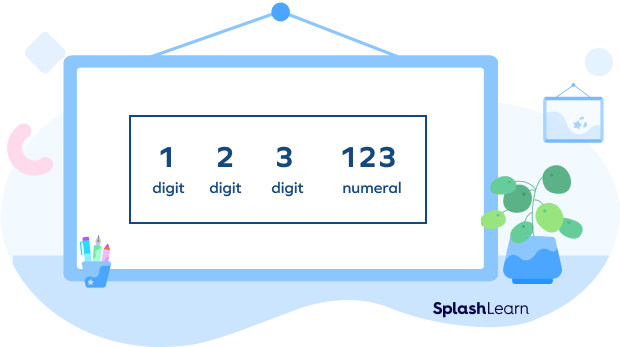
Digit Definition in Math
Digits are the single numbers used to represent values in math. 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 are used in different combinations and repetitions to represent all the values in math.
Any of the ten numbers from 0 to 9 can be represented by a symbol known as a digit.
An example of a two-digit (2-D) number is 65. It is made up of the 6 and 5.
Recommended Games
History
In ancient times, people did not have a number system or numerals to measure or count things. As the world expanded its roots into subjects like science and the trade between nations grew, an urgent requirement for a uniform numeric system came. Thus, digits were formed and combined for use in different situations.
We use international numerals like “123” and “65”, but the Romans used Roman numerals, and there have been many other numerals used throughout history.

Recommended Worksheets
Place Value
In math, every digit in a number has a place value. Place value can be defined as the value represented by a digit in a number on the basis of its position in the number.
For example, the place value of 7 in 3743 is 7 hundreds or 700. However, the place value of 7 in 7432 is 7 thousands or 7000. Here, we can see that even though the 7 is the same in both numbers, its place value changes with the change in its position.
Face Value
Place value and face value are not the same. The face value of a digit is the value of the digit whereas the place value of a digit is its place in the number. In simple words, the face value tells the actual value whereas the place value tells the value based on its position. Hence, the face value of the digit never changes irrespective of its position in the number, whereas its place value changes with the change in its position.
For example, the face value of 2 in both the numbers 283 and 823 is 2. Whereas, the place value of 2 is 200 in 283 and 20 in 823.
Example of digit numbers:
- Two-digit Numbers
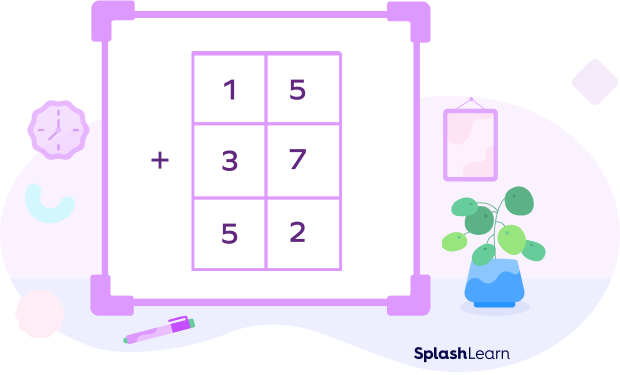
Two-digit numbers begin from 10 and end at 99. The tens place should be between 1 and 9.
Consider two numbers, 15 and 37. When these two numbers are added, they give a new number, 52.
15 + 37 = 52
- Four-digit Numbers
When four digits are written together, a four-digit number is formed. The range of these numbers is from 1000 to 9999.
Consider the numbers 1001, 2001, 5000, and 1040. When these numbers are added, they give a new four-digit number, 9042.
$1001 + 2001 + 5000 + 1040 = 9042$
Similar to the examples mentioned above, as the digits increase in a number, its value increases. For example, 10,000 is a 5-D number whose value is more than all 4 – D natural numbers.
Solved Examples
Example 1: How many digits are there in 1458?
Solution: The number 1458 has four digits that are 1, 4, 5, and 8.
Example 2: Using the digits 6, 6, 8, get the greatest $3-$digit number.
Solution: The greatest $3-$digit number that can be formed with these is 866.
Example 3: What is the place value of digit 4 in the number 84,527?Solution: The place value of 4 in 84,527 is 4000 (four thousand).
Practice Problems
Digit in Math - Definition with Examples
Which of these make the greatest three-digit number?
Greatest three digit number is 999 made up of 9 repeated three times.
Which of these is at the ten thousands place in the number 783,425?
8 is in the ten-thousands place.
Which is a decimal number in 36.2?
In the given number, 2 is placed after the decimal point. Hence it is a decimal number.
Frequently Asked Questions
What is the difference between decimals and digits?
The term digits refer to a collection of real numbers, including zero and all positive counting numbers. Fractions, negative integers, and decimals are not treated as digits.
The decimal is a number that is placed on the right-hand side after the point (.) in a number.
For example, in the number 23.8, 8 is a decimal number.
Which digits are used to make numerals?
0 to 9 are used in different combinations to make numerals.
Are fractions a part of digits?
Fractions represent specific parts of a whole significant digit. They lie in between two significant numbers. They are a part of the number system but not necessarily a part of significant digits.
Who introduced the concept of a digit?
There is no specific name. It is believed that zero was first used in 4 CE by the Mayans.




































