What Is a Factor Tree?
A factor tree is a diagram that breaks down a composite number into its prime factors. It starts with the given number at the top and branches out, with each branch representing a factor of the previous number. This process continues until all the branches reach prime numbers. The last numbers (leaf nodes) represent the prime factorization of the original number.
The general method to find the prime factorization can be tedious for large numbers. Factor tree provides a quick, simple, and systematic way to understand the prime factorization of numbers.

What Are Factors?
A factor is a number that divides a given number evenly without leaving a remainder.
When we multiply two numbers to find the product, both the numbers being multiplied are called factors of the product.
Example:
1 × 15 = 15
3 × 5 = 15
So, 15 has four factors: 1, 3, 5, and 15.
However, this method can be inconvenient for larger numbers. That’s where the factor tree method comes in.
Recommended Games
Factor Tree: Definition
A factor tree is a visual representation or a diagram that breaks down a given number into its prime factors. It is a prime factorization method, which expresses a composite number as a product of prime numbers.
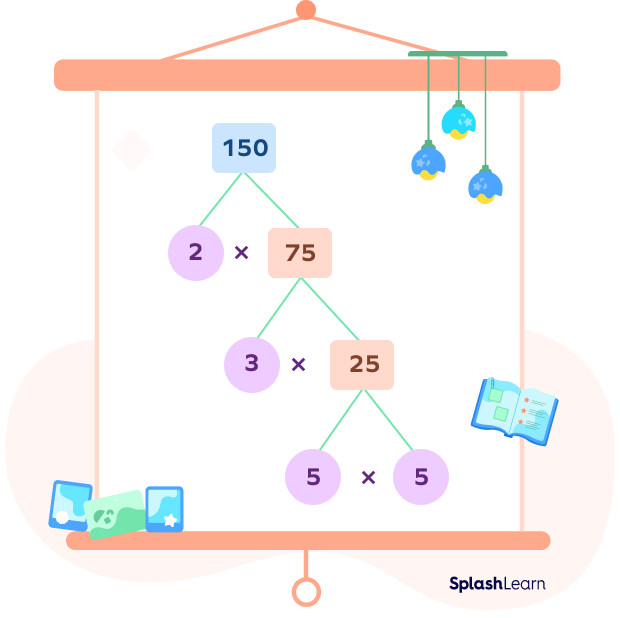
Recommended Worksheets
What Is Splitting Numbers and Branching?
- Splitting Numbers in a Factor Tree:
Splitting numbers in a factor tree refers to breaking down a composite number into its factors.
When you start with a composite number as the root of the factor tree, you split it into two or more factors along branches.
These factors can be prime or composite, and the process continues until you reach prime factors at the end of the branches.
- Branching in a Factor Tree:
Branching in a factor tree involves extending lines or branches from a number to represent its factors or divisors. Each branch represents one of the factors of the number from which it originates. The branching process continues until all factors are expressed as prime numbers, creating a visual representation of the prime factorization of the original composite number.
In summary, splitting numbers involves breaking down a composite number into its factors, while branching represents the visual connections between these factors in a factor tree, ultimately leading to the prime factorization of the original number.
Example: We can express 120 as the product of 12 and 10.
120 = 12 × 10
Both 12 and 10 are, again, composite numbers.
12 = 4 × 3
10 = 2 × 5
Next, we can write 4 as
4 = 2 × 2
Now, we have reached the end since we obtained all the prime factors, 2, 3, 4, and 5.
How to Draw a Factor Tree of a Number
Step 1: Write the composite number at the top of the tree. (This number is often termed as the root number of the factor tree.)
Step 2: Identify two numbers that multiply together to give the root number. These factors can be prime or composite.
Step 3: Determine if the factor is prime or composite for each branch.
If it’s composite, continue branching until you reach prime factors.
Step 4: Continue this process for each composite factor, branching out and factoring until you have expressed all factors as primes.
Step 5: The factor tree is complete when there are prime numbers at the end of each branch.
Note: To create a systematic pattern, encircle the prime factors and draw a box around the composite factors.
Factor Tree Examples:
Example 1: Factor tree of 120

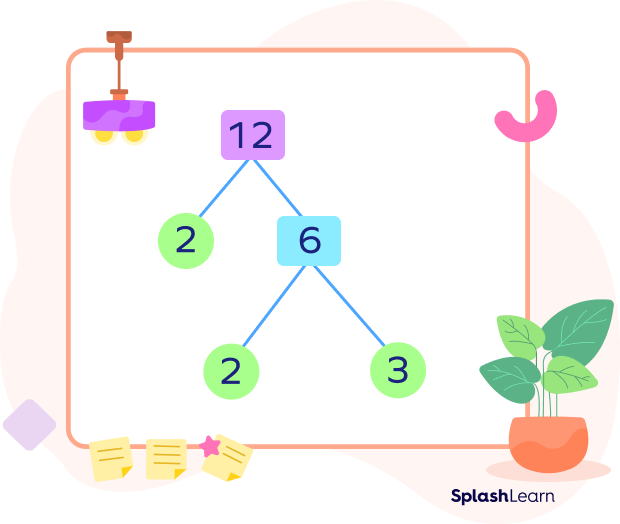
Example 2: Factor tree of 12
Find the factor tree of 12.
12 = 2 × 6
2 is prime. 6 is composite.
12 = 2 × (2 × 3)
Thus, 12 = 2 × 2 × 3
12 = 22 × 3
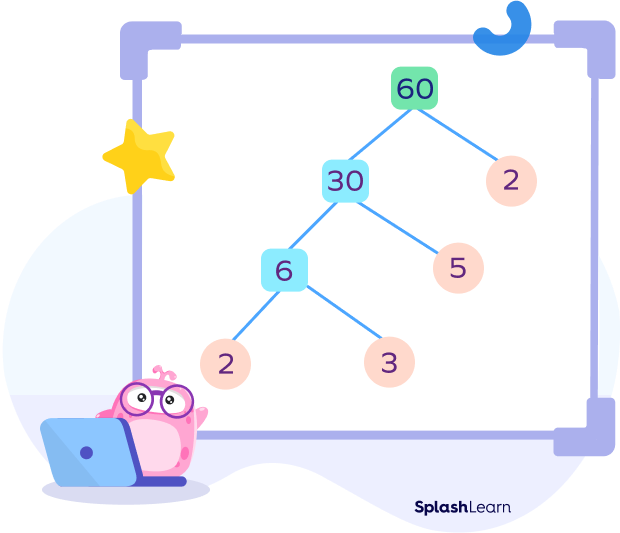
Example 3: Factor tree of 60
60 = 2 × 30
60 = 2 × 3 × 5 × 2
60 = 2 × 2 × 3 × 5
Prime Factor Tree
A prime factor tree specifically aims to find the prime factorization of a composite number. The focus is solely on breaking down the number into its prime components.
The primary purpose of a prime factor tree is to express a composite number as a product of its prime factors, simplifying it to its prime form.
A prime number is a natural number with only two factors: 1 and the number itself.
Examples: 2, 3, 5, 7,…
Example 1: Find the prime factorization of 72
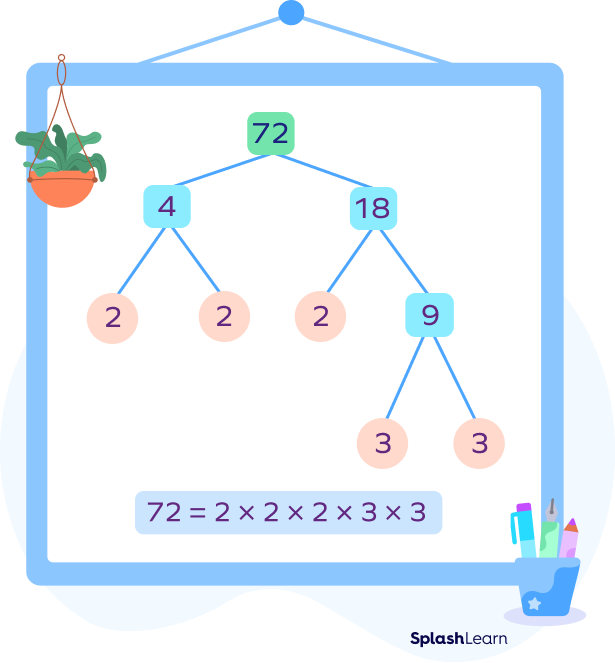
Example 2: Factor tree of 180
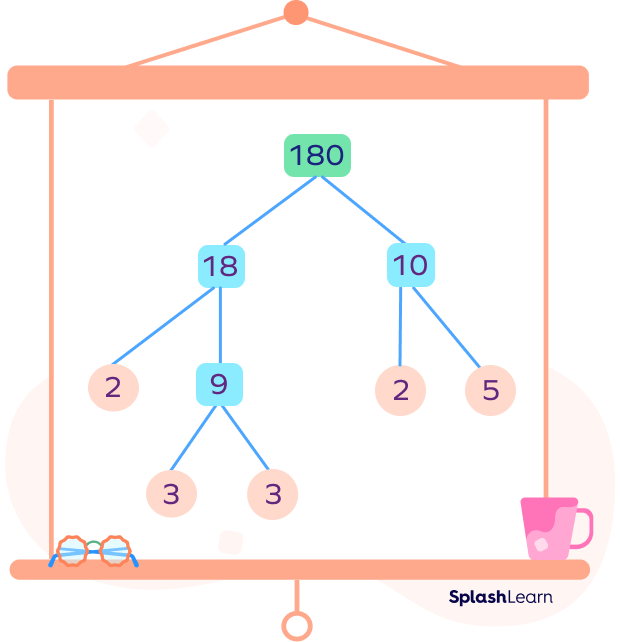
NOTE: A number can have multiple factor trees, which ultimately give the same prime factorization. The prime factorization is unique, but a factor tree can have different forms depending on how you break down the number.
Here are two different factor trees of 64:
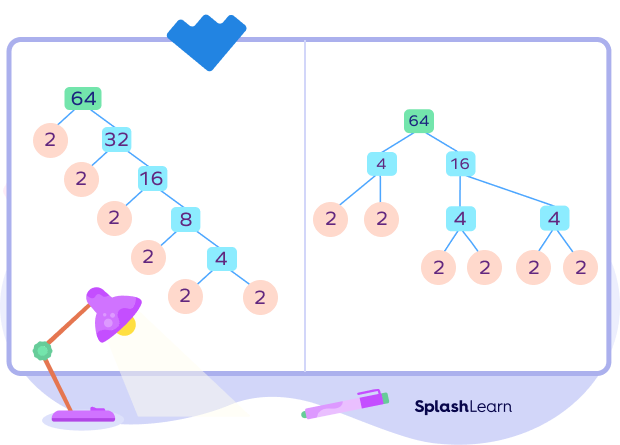
Prime factorization of 64 = 26
Applications of a Factor Tree
1) To find the prime factors of a number
2) To write the prime factorization of a number
3) To find the GCD (Greatest Common Divisor) of a number
4) to find the LCM (Least Common Multiple) of a number
Facts about Factor Trees
- The endpoints of the tree represent prime factors, as they cannot be further factored. They are also called “leaf nodes.”
- The prime factorization of any number is always unique. However, the factor
Conclusion
In this article, we learned about Factor Trees, a method for finding a number’s prime factors. We discussed how to draw a factor tree, its applications, and associated concepts. Let’s solve a few examples for better comprehension and reinforcement.
Solved Examples on Factor Trees
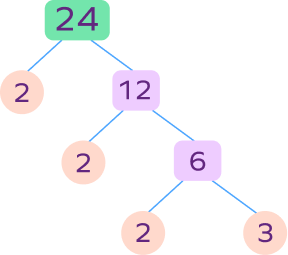
1. Draw a factor tree for 24.
Solution:
24 = 2 × 12
24 = 2 × 2 × 6
24 = 2 ×2 × 2 × 3
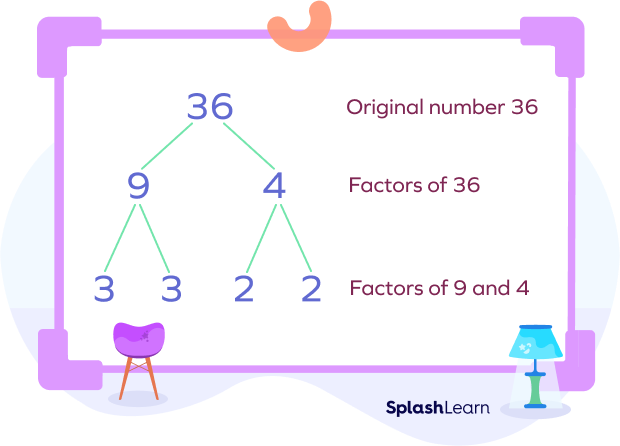
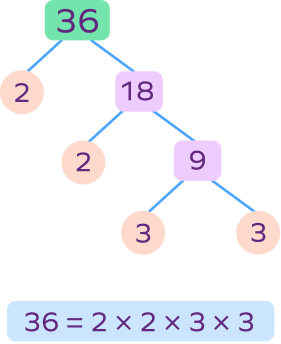
2. Write the prime factorization of 36 using a factor tree.
Solution:
Here’s the factor tree and prime factorization of 36:
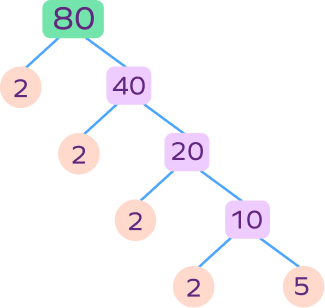
3. Draw a factor tree for 80.
Solution:
Factor tree of 80:
4. Write the prime factors of 156 using the factor tree method.
Solution:
Here’s a factor tree of 156:
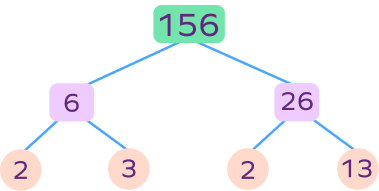
Prime factors of 156: 2, 3, and 13
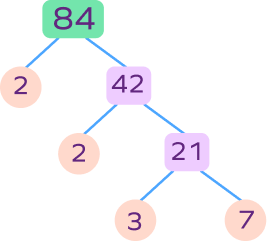
5. Draw a factor tree of 84.
Solution:
Factor tree of 84:
Practice Problems on Factor Trees
Factor Tree – Definition with Examples
Find the missing number in the factor tree of 125.
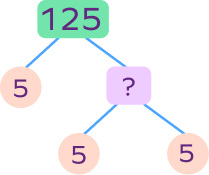
There are two ways to find the missing numbers.
Divide 125 by 5.
$125 \div 5 = 25$
OR multiply two numbers forming the two branches.
$5 \times 5 = 25$
A prime number has ___ factors.
A prime number has only two factors.
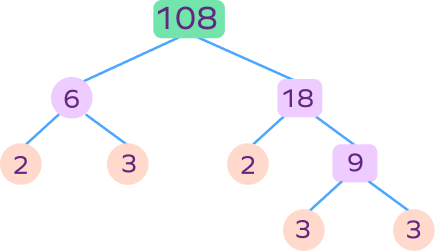
Which of the following prime factorizations are correct?
Prime factorization of $108 = 2 \times 2 \times 3 \times 3 \times 3$
Write the prime factorization of 92 using the given factor tree.
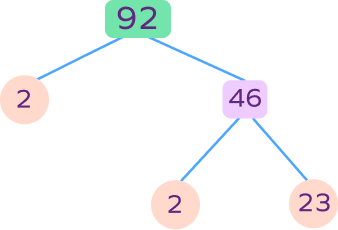
$92 = 2 \times 2 \times 23$
Frequently Asked Questions about Factor Trees
What are factor trees?
Factor trees are a visual way to show how numbers can be broken down into their prime factors (numbers divisible only by 1 and themselves).
How do I make a factor tree?
- Start with your number at the top. Find two factors that multiply to make that number. Write them below, branching out like a tree.
- Repeat for each factor, breaking them down further until you reach prime numbers.
What are prime numbers?
Prime numbers are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11).
What are some uses of factor trees?
- Finding prime factors of a number.
- Checking if a number is prime.
- Finding the least common multiple (LCM) or greatest common factor (GCF) of two numbers (more advanced).




























