Prime Factorization: Definition, Methods, Examples, FAQs

What Is Prime Factorization in Math?

Prime factorization of a number is a way of writing a number as the product of its prime factors. Thus, the meaning of prime factorization of a number is finding prime numbers which when multiplied together give us the required number.

Example: The product prime numbers 2, 3, and 5 is 30.

Prime factorization of $30 = 2 \times 3 \times 5$

Prime Factorization Definition

Prime factorization can be defined as a way of expressing a given number as the product of its prime factors. 

If a prime number occurs more than once, we write it using exponents.

Example: Prime factorization of $18 = 2\times3\times3 = 2\times3^{2}$

What Are Factors and Prime Factors?

A factor of a number is a number that divides the given number exactly, leaving no remainder.

Prime numbers are numbers that have only two factors, 1 and the number itself. Examples of prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, and so on.

Consider an example. The numbers 1, 2, 3, 6 are factors of the number 6.

Thus, we can say that 2 and 3 are the prime factors of 6 and express 6 as 

$6 = 2\times3$

Here, we expressed 6 as the product of its prime factors. When we write a number as a product of all its prime factors, it is called prime factorization. 

How to Find Prime Factorization of a Number

The most common methods that are used for prime factorization are:

• Prime Factorization by Factor tree method
• Prime Factorization by Division method

We will discuss these methods in detail. However, we can also find prime factors of a number by simply breaking down the number using its factors until we get prime numbers. 

Example: Find prime factorization of 48.

$42 = 8\times6$

$42 = (2\times2\times2)\times(2\times3)$

$42 = 2^{4}\times3$

Prime Factorization Methods

You can find the prime factorization of a number using various methods.

Let’s discuss the two important methods to solve prime factorization problems.

• Factor tree method
• Division method

Let us look at both the methods in detail.

Factor Tree Method

In the factor tree method, we first break down the number using the smallest prime factor of the number. The composite factors obtained in the process are further broken down until we reach the prime factors. 

The factors of the given number written in this way look like a tree. The prime numbers obtained in the end are called leaf nodes of the factor tree.

Example: Find the prime factorization of 250 using the factor tree method.

Step 1: Place the number 250 on top of the factor tree.

Step 2: Break down the given number using its smallest prime factor.

Here, $250 = 2 \times 125$

Step 3: Factorize the composite factor obtained in step 2. 

$125 = 5 \times 5$

Repeat the same step until we get all prime factors in the end. 

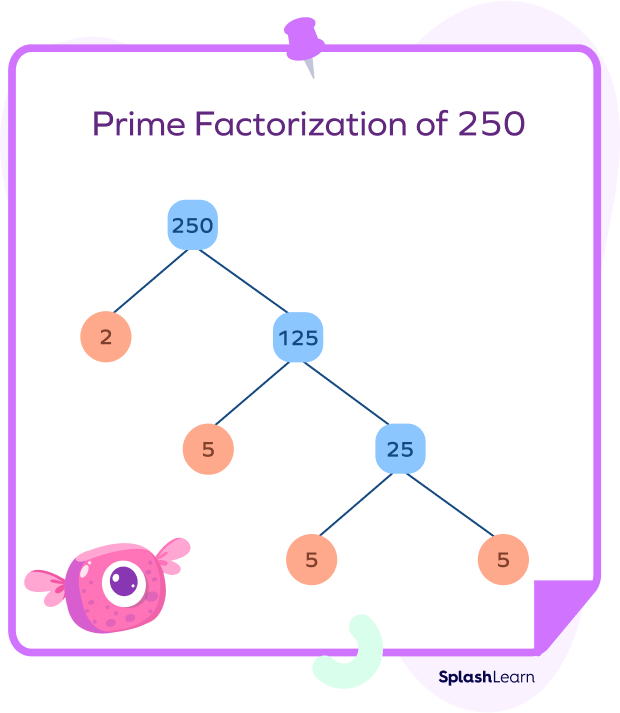
Thus, prime factorization of $250 = 2 \times 5^{3}$

Division Method

Step 1: Divide the given number by its smallest prime factor. 

Step 2: Divide the quotient obtained by its smallest prime factor.

Step 3: Repeat the process until the quotient becomes 1.

Step 4: Multiply all the prime factors.

Example: Prime factorization of 28 using division method.

Why Find Prime Factors?

As we already know that a prime number can only be divided by 1 or the number itself, so it cannot be factored any further. A composite number can be broken down using prime numbers and can be written uniquely as a product of its prime factors.

The prime numbers are the basic building blocks of any number.

We have many real-life uses of this concept while dealing with large numbers, such as in cryptography.

What Are the Applications of Prime Factorization?

• Finding square roots of perfect squares

It’s very easy to find square roots of perfect squares using prime factorization. 

Consider an example.

Prime factorization of $1225 = 5\times5\times7\times7$

$\sqrt{1225} = \sqrt{5\times5\times7\times7}$

$\sqrt{1225} = 5\times7$

$\sqrt{1225} = 35$

• Encryption or cryptography 
• Finding HCF and LCM using prime factorization
• Mental arithmetic
• Studying patterns

Finding HCF and LCM Using Prime Factorization

HCF (Highest Common Factor): The largest number of all the common factors of two numbers.

LCM (Least Common Multiple): The smallest number of all the common multiples of two numbers.

The HCF and LCM of two numbers can be calculated using the prime factorization method. It is quite useful when dealing with two or more large numbers. 

• First find the prime factorization of both the numbers. 
• HCF is the product of the smallest power of each common prime factor.
• LCM is the product of the greatest power of each prime factor.

Let us understand these points with the help of an example.

Example 1: Find the HCF and LCM of 42, 72, and 120 using prime factorization.

We will first find the prime factorization of the given numbers.

$42 = 2 \times 3 \times 7$

$72 = 2^{3} \times 3^{2}$

$120 = 2^{3} \times 3 \times 5$

HCF $=$ Product of the common prime factors with the lowest degree. 

HCF (42, 72, 120) $= 2 \times 3 = 6$

LCM = Product of the greatest powers of all prime factors.

LCM (42, 72, 120) $= 2^{3} \times 3^{2} \times 5 \times 7 = 2520$

Example 2: What is the HCF and LCM of 50 and 75?

We will first find the prime factorization of the given numbers.

The prime factorization of $50 = 2 \times 5^{2}$

The prime factorization of $75 = 3 × 5^{2}$

HCF $=$ Product of the common prime factors with the lowest degree. 

Multiply all the common prime factors with the lowest degree (power).

Here, we have only 5 as a common prime factor with the lowest power of 2.

Hence, HCF of (50, 75)$ = 5^{2} = 25$

LCM = Product of the greatest power of each prime factor.

Multiply all the prime factors with the highest degree.

Hence, LCM of (50, 75) $= 2^{1} \times  3^{1} \times 5^{2} = 150$

Prime Factorization of a Number

Take a look at the table showing prime factorization of some numbers.

Number	Prime Factorization
32	$2^{5}$
60	$2^{2}\times3\times5$
48	$2^{4}\times3$
30	$2\times3\times5$
92	$2^{2} × 13$
42	$2 \times 3 \times 7$
18	$2 \times 3^{2}$
45	$3^{2} \times 5$
72	$2^{3}\times3^{2}$
105	$3 \times 7 \times 5$
24	$2^{3} \times 3$

Facts about Prime Factorization

Conclusion

In this article, we learned about factors, prime factors, prime factorization, methods of prime factorization, and how to find HCF and LCM using prime factorization. Let’s solve a few examples and practice problems for better understanding and revision!

Solved Examples on Prime Factorization

1. Find the prime factorization of 24 using the factor tree method.

Solution:

Let us look at the steps to find the prime factorization of 24 using the factor tree method:

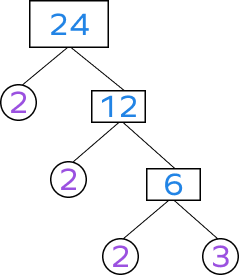
Therefore, the prime factorization of $24 = 2^{3} \times 3$.

2. Find the prime factorization of 42 using the division method.

Solution: 

Divide 42 by its smallest prime factor. Next, divide the quotient by its smallest prime factor. Repeat this process until we get 1 as a quotient.

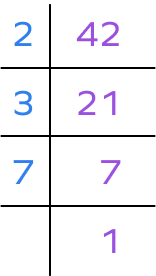
Prime factorization = Product of all prime factors

Therefore, the prime factorization of $42 = 2 \times 3 \times 7$.

3. Find the HCF of 100 and 250 using prime factorization.

Solution:

To find the HCF of any number using prime factorization, we first need to find the prime factorization of both the numbers.

Prime factorization of $100 = 2^{2} \times 5^{2}$

Prime factorization of $250 = 2^{1} \times 5^{3}$

HCF $=$ Product of the common prime factors with the lowest degree. 

HCF (100, 250) $= 2^{1}\times 5^{2}$

Therefore, the Highest Common Factor of 100 and $250 = 50$. 

4. Find the LCM of 100 and 250 using prime factorization.

Solution:

To find the LCM of any number using prime factorization, we first need to find the prime factorization of both the numbers.

Prime factorization of $100 = 2^{2} \times 5^{2}$

Prime factorization of $250 = 2^{1} \times 5^{3}$

LCM = Product of the greatest power of each prime factor.

LCM(100, 250) $= 2^{2} \times 5^{3}$

Therefore, the LCM of 100 and $250 = 2^{2} \times 5^{3} = 500$.

5. Write all the prime factors of 1250 using the division method.

Solution:

To find the prime factors of a number, we need to find the prime factorization using one of the two methods.

Let us solve this by the division method.

Now, $\frac{1250}{2} = 625$

          $\frac{625}{5} = 125$

          $\frac{125}{5} = 25$

           $\frac{25}{5} = 5$

           $\frac{5}{5} = 1$

The prime factors of 1250 are 2 and 5. 

The prime factorization is $2 \times 5^{4}$.

Practice Problems on Prime Factorization

Frequently Asked Questions on Prime Factorization