What Is 3-digit Multiplication?
The 3-digit multiplication refers to multiplication problems involving three-digit numbers.
Three-digit numbers (100-999) have only three digits, placed at three place values: Hundreds, Tens, and Ones.
In this article, we will discuss
- 3-digit by 1-digit multiplication
- 3-digit by 2-digit multiplication
- 3-digit by 3-digit multiplication
Recommended Games
How to Solve the 3-digit Multiplication
The column method or the long multiplication method is convenient and the most commonly used method to carry out three-digit long multiplication.
Step 1: Write the two numbers one below the other, preferably the larger number on top and the smaller number below, such that their place values are aligned.
The number placed on top (the first number) is called a multiplicand, and the number written below (the second number) is called the multiplier.
Step 2: Multiply each digit of the multiplier with all the digits of the multiplicand one by one starting from the ones digit, followed by the tens digit, and then the hundreds digit.
These products are called partial products.
Step 3: Add all the partial products to find the final answer.

Recommended Worksheets
3-digit by 1-digit Multiplication
There are two cases to consider when a three-digit number is multiplied by a one-digit number.
- 3-digit by 1-digit multiplication without regrouping (No carry-overs)
To multiply a three-digit number and a one-digit number, we multiply the one-digit number by all the digits of the three-digit number.
If the product of the one-digit number with each digit of the 3-digit multiplicand is a single digit, then there is no hassle of carrying over.
Example: 1323
We multiply each digit of 132 by 3.
Multiplying (ones digit) 2 with 3, we get 3 ✕ 2 = 6
Multiplying (tens digit) 3 with 3, we get 3 ✕ 3 = 9
Multiplying (hundreds digit) 1 with 3, we get 3 ✕ 1 = 3

- 3-digit by 1-digit multiplication with regrouping (carry over involved when we get a product greater than 9)
When multiplying digits of the multiplicand with the one-digit number, if we get a product greater than 9, we have to use regrouping. Let’s understand with the help of an example.
Example: Multiply 456 by 2.
Arrange 456 and 2 one below the other such that their place values are aligned (2 is aligned with 6).
Step 1: Multiply 2 with the ones digit of 456, which is 6.
6 ✕ 2 = 12
Since 12 is a two-digit number, we write 2 under the ones column and carry 1 to the next place (tens column).
- How does the regrouping in multiplication work?
Regrouping in multiplication, similar to addition, involves managing the numbers that exceed the base value of a place (which is 10 in our decimal system). - Since 12 is a two-digit number that exceeds the base of 10, we must regroup.
- Here, we are splitting 12 as 12 = 10 + 2.
- We write 2 at the ones place. (The place value of 2 at ones place = 2 ✕ 1=2)
- Next, we carry over the 1 to the tens place. (The place value of 1 at tens place is 10.)
Write the carry-over 1 in the tens column, right above 5.
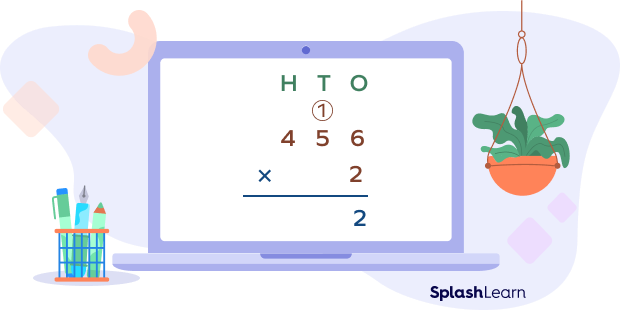
Step 2: Now, multiply 2 with the next digit (tens digit) of 456, which is 5.
5 ✕ 2 = 10
Add the carry-over 1.
10 + 1 = 11
Write 1 at the tens place and carry 1 over to the hundreds place.
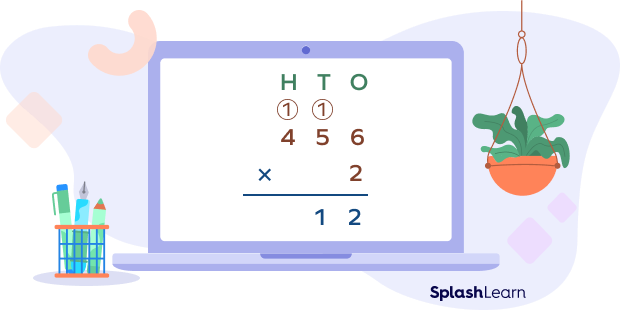
Step 3: Finally, multiply 2 with the next digit (hundreds digit) of 456, which is 4.
4 ✕ 2 = 8
Add the carry-over 1.
8 + 1 = 9
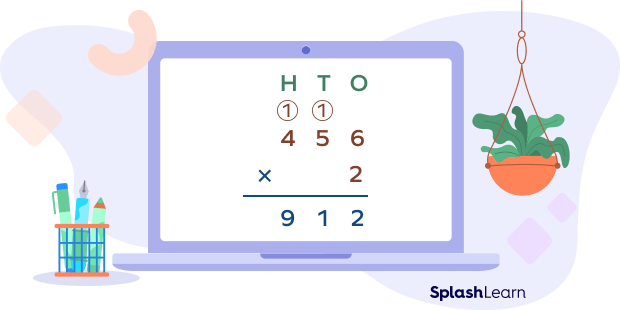
Thus, 456 ✕ 2 = 912
3-digit by 2-digit Multiplication
Let’s learn how to multiply 3-digit numbers by 2-digit numbers. The process is similar to the steps we discussed in the previous section. Here, we add one more step: multiply the second digit (tens digit) of the multiplier with all the digits of the multiplicand (three-digit number).
We come across similar cases: grouping and no regrouping.
- 3-digit by 2-digit multiplication without regrouping
Let’s understand the steps with the help of an example.
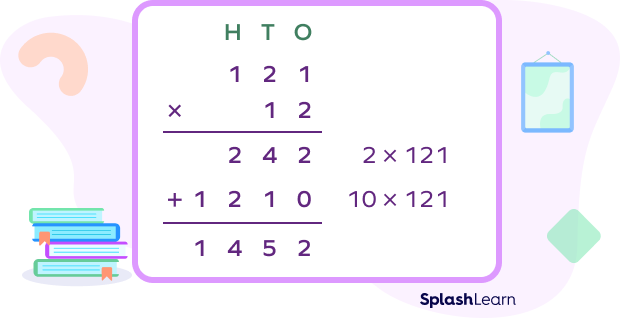
Example: Multiply 121 by 12.
Arrange the numbers 121 and 21 in columns such that their place values are aligned.
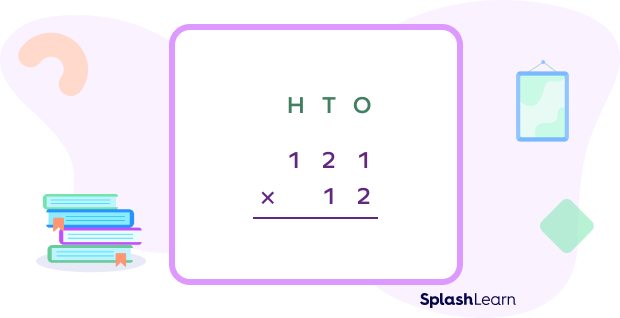
Step 1: Multiply 1 by each digit of 121 to find the first partial product.
2 ✕ 1 = 2
2 ✕ 2 = 4
2 ✕ 1 = 2
242 is the first partial product.
Step 2: The second partial product is the product of 10 and 121.
Write 0 in the ones place of the second partial product.
Multiply 1 by each digit of 121.
1 ✕ 1 = 1
1 ✕ 2 = 2
1 ✕ 1 = 1
1210 is the second partial product.
Add the two partial products to obtain the final answer.
242 + 1210 = 1452
Thus, 121 ✕ 12 = 1452
Let’s summarize it!
- 3-digit by 2-digit multiplication with regrouping
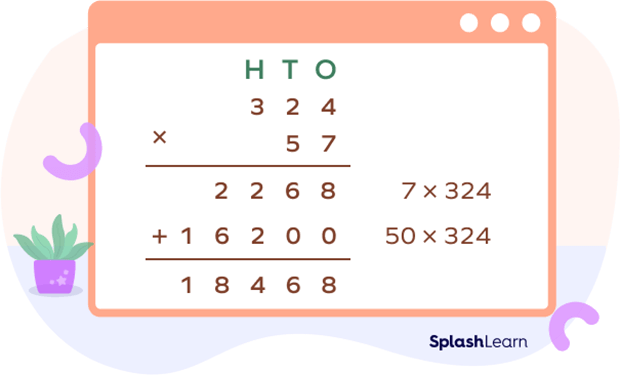
The concept of regrouping remains the same regardless of the type of multiplication. We just need to take care of the place values of the digits.
Example: 324 ✕ 57
3-digit by 3-digit Multiplication
Let’s learn how to multiply 3-digit numbers by 3-digit numbers. It takes us one step ahead of three-digit by two-digit multiplication, adding another partial product in the process.
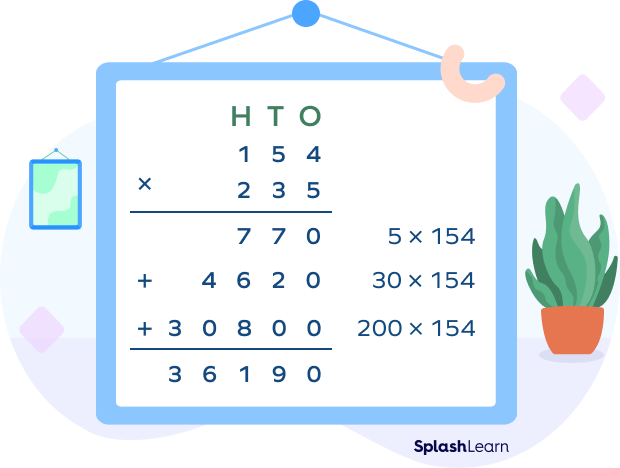
Example: Multiply 154 by 235.
Here, we will find
1st partial product = 154 ✕ 5
2nd partial product = 154 ✕ 30
3rd partial product = 154 ✕ 200
Box Method for Three-digit Multiplication
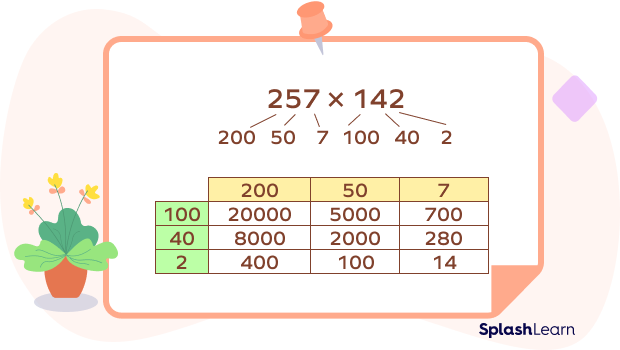
The box method, also known as the area model, is a visual method for solving three-digit multiplication problems. It helps break down the multiplication into smaller, more manageable steps.
In this method, we break down the two numbers using their place value, arrange the expanded form of numbers in a rectangular grid, and write the partial products in their respective boxes. Finally, add all the partial products together to find the final product.
If you are looking for 3-digit multiplication tricks, this method is for you!
Example: 257 ✕ 142
257 ✕ 142 = 20000 + 5000 + 8000 + 2000 + 700 + 400 + 100 + 280 + 14 257 ✕ 142 = 36,494
Facts about Three-digit Multiplication
- Three-digit numbers range from 100 to 999. The multiplication of the smallest three-digit number (100) and the greatest three-digit number (999) is 999100=99,900.
- Three-digit multiplication helps students better understand math concepts such as place values, partial products, addition, etc. With more practice, it also helps students carry out error-free calculations.
- Practice and repetition are key to improving speed and efficiency in three-digit multiplication.
- When multiplying 3 numbers, the simplest way is to multiply any two numbers and the resulting product with the remaining third number.
- Multiplication is commutative. Thus, the order of numbers does not matter.
Conclusion
In this article, we learned three-digit multiplication methods and how to do three-digit multiplication with and without regrouping. We discussed steps for each category with examples. Let’s go through a few more examples for better comprehension and hands-on practice.
Solved Examples on 3-digit Multiplication
1. What is the product of 142 by 7?
Solution:
Let’s use the long multiplication (column) method.
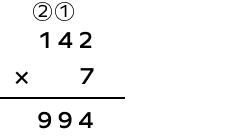
Thus, the product of 142 and 7 is 994.
2. Find the product of 235 by 37.
Solution:
37 = 30 + 7
First partial product: 235 ✕ 7 = 1,645
Second partial product: 235 ✕ 30 = 7,050
Adding the partial products, we get
1,645 + 7,050 = 8,695
Thus, 235 ✕ 37 = 8,695

3. What is the result when 376 is multiplied by 100?
Solution:
Multiplication of a number with any power of 10 is easy.
Simply write the number of zeros equal to the power of ten in front of the given number.
376 ✕ 100 = 37,600
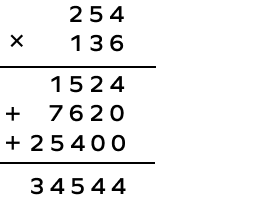
4. What is the product of 254 by 136?
Solution:
136 = 100 + 30 + 6
By multiplying 254 by 6 using regrouping, we get 1,524.
By multiplying 254 by 30 and regrouping, we get 7,620.
By multiplying 254 by 100, we get 25,400.
On adding the partial products, we get
235 ✕ 136 = 25,400 + 7,620 + 1,524 = 34,544
5. Find the product of the smallest two-digit number and the greatest three-digit number.
Solution:
Smallest two-digit number = 99
Greatest three-digit number = 999
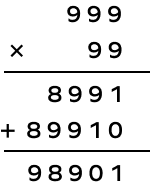
Practice Problems on 3-digit Multiplication
3-digit Multiplication
On multiplying 409 by 8, we get ____.
$409 \times 8 = 3275$
Product $= 3272$
Find the product of 654 by 14.
$14 = 10 + 4$
On multiplying 654 by 4 using regrouping, we get 2,616.
On multiplying 654 by 10 using regrouping, we get 6,540.
$2616 + 6540 = 9,156$
The product of 306 and 77 is ____.
$77 = 70 + 7$
$306 \times 7 = 2,142$
$306 \times 70 = 21,420$
$21,420 + 2,142 = 23,562$
Which of the following is the product of 981 by 19?
$19 = 10 + 9$
$981 \times 9 = 8,829$
$981 \times 10 = 9,810$
$8,829 + 9,810 = 18,639$
The product of 592 by 301 is ___.
$301 = 300 + 0 + 1$
$592 \times 1 = 529$
$592 \times 0 = 0$
$592 \times 300 = 177,600$
$592 + 0 + 177,600 = 178,192$
Frequently Asked Questions about 3-digit Multiplication
How many positive three-digit numbers are there?
Smallest three-digit number = 100
Greatest three-digit number = 999
Common difference = d = 1
First term = a = 100
nth term = 999 = a + (n − 1) d
999 = 100 + (n − 1) (1)
899 = n − 1
n = 900
What skills can you develop by practicing three-digit multiplication?
Three-digit multiplication helps with numerical fluency, mental math skills, and problem-solving abilities, preparing students for more advanced mathematical concepts.
When do we use regrouping in three-digit multiplication?
Regrouping, also known as carrying over, is used in three-digit multiplication when the product of multiplying the digits in a particular place value position exceeds 9.
How can I practice three-digit multiplication?
Practice regularly using worksheets, online math games, or flashcards. Start with simpler problems and gradually increase the complexity. You can also use real-life examples to apply three-digit multiplication, such as calculating prices or quantities.




































