Multiplication – Definition with Examples

$8 + 8 = ?$

$8 + 8 + 8 + 8 = ?$

$8 + 8 + 8 + 8 + 8 + 8 + 8 = ?$

Don’t you think it’s too tedious to add 8 so many times. 

There is an easy and better way to do this. 

Multiplication Definition in Math

Multiplication is one of the four basic arithmetic operations, alongside addition, subtraction, and division. In math, multiply means the repeated addition of groups of equal sizes. 

To understand better, let us take a multiplication example of the ice creams.

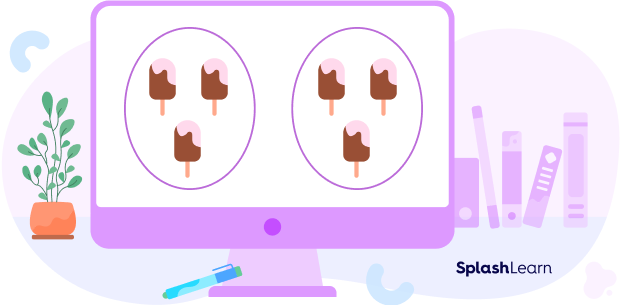
Each group has ice creams, and there are two such groups. 

Total ice creams are $3 + 3 = 6$. 

However, you have added two groups of 3 ice creams. Therefore, you have multiplied three ice creams by two. You may also write it as $2 \times 3 = 6$.

As we can see, $3 + 3$ is the same as $2 \times 3$.When we multiply two numbers, the answer is called product. The number of objects in each group is called multiplicand, and the number of such equal groups is called the multiplier. In our case, $3$ is the multiplicand, $2$ is the multiplier and 6 is the product.

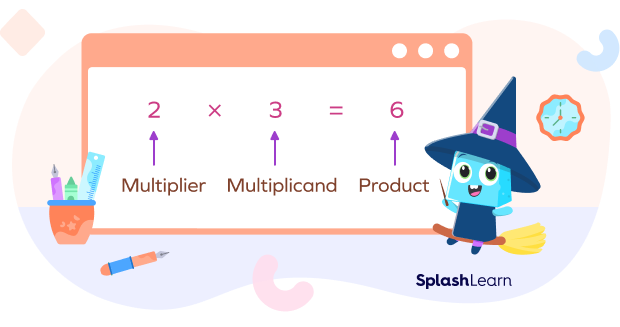
There are many ways to read an equation that involves multiplication. 

For example, $2 \times 3 = 6$. It can be read as follows:

• Two multiplied by three is six.
• Two times three is six.
• Two threes are six. 

Symbol of Multiplication

Multiplication is represented by the signs cross (×), asterisk (*), or dot (·). While writing in your notebooks, you are most likely to use the cross. The asterisk and dot are used in computer languages and algebra (higher mathematics). 

For example: $6 \times 5 = 30$

$7 * 8 = 56$ 

$5 · 4 = 20$

Multiplying Integers

In order to multiply the integers, we need to see the sign of the integers. 

• Multiply two positive integers

The product of the two positive integers is always a positive integer.

For example: $5 \times 6 = 30$

• Multiply one positive and one negative integer

The product of a positive and negative integer is always a negative number. 

For example: $(-$ $5) \times 6 = (-$ $30)$

• Multiply two negative integers

The product of two negative integers is always a positive integer. 

For example: $(-$ $5) \times ( -$ $6) = 30$

Multiplying Fractions

In order to multiply the fractions, the numerators and denominators are multiplied together such that:

$\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}$

For example: Multiply $\frac{1}{2}$ and $\frac{3}{4}$.

$\frac{1}{2} \times {3}{4} = \frac{1 \times 3}{2 \times 4} = 38$

Multiplying Decimals

Multiplying the decimals is the same as multiplying the integers. 

For example: Multiply $13.2$ and $3.5$. 

Let us multiply $13.2$ and $3.5$ by removing the decimals here and consider them whole numbers. Hence,

$132 \times 35 = 4620$

We put the decimal point back, then the product of the two decimal numbers will have decimal up to two positions from right to left, such that

$13.2 \times 3.5 = 46.20$

Multiplying Numbers with Powers

In math, powers define a base raised to the exponent. For example: $3^2, {(-5)}^4$.

1. When the base is the same but power is different

Let the two expressions be $x^m$ and $x^n$. Here, the base is “x”. 

When the terms with the same base are multiplied, the powers gets added, i.e., $x^m$ $x^n = x^{(m + n)}$

For example: $3^2$ $3^5=3^{2+5} = 3^7$

2. When the base is different but the exponent is the same

Let the two expressions be $x^m$ and $y^m$. Here, the power is “m”. 

When the terms with the same exponents are multiplied, the bases are multiplied first and then we apply the exponent, i.e., $x^my^m = (xy)^m$ 

For example: $3^24^2=(3 \times 4)^2=12^2 = 144$

3. When the bases and powers are different

Let the two expressions be xn and ym. Here, the bases are x and y. The powers are n and m. When we multiply these expressions, each expression is evaluated separately and then multiplied. It can be written mathematically as

$x^ny^m = (x)^n(y)^m$

            For example: $3^2 \times 4^3=9 \times 64 = 576$

Properties of Multiplication

Just like addition, multiplication also follows specific properties, which are as follows: 

1. Commutative Property: This property states that when we multiply two numbers, the order will not cause any change in the product.

Let us consider $2 \times 3 = 6$, for example. If we reverse the order, i.e., compute $3 \times 2$, the answer will still be $6$. 

2. Associative Property: This property states that if we multiply three numbers or more, one after the other, the order does not matter. For example: if we have to $2, 3$ and $4$:

• $(2 \times 3) \times 4 = 24$
• $2 \times (3 \times 4) = 24$

If you jumble the order and multiply, the result will still not change.

• $3 \times (2 \times 4) = 24$

3. Distributive Property: This property states that if you multiply a number by the sum of two numbers, the result will be equal to the sum of products you obtain by multiplying that number by those two numbers individually. For example, $3 \times 8$.

• You can write $8$ as $6 + 2$. Therefore $3 \times 8 = 3 \times (6 + 2) = 24$
• Now, $3 \times 6 = 18$. Also, $3 \times 2 = 6$.
• $18 + 6 = 24 = 3 × 8$. Therefore, distributive property holds true.

Tips to Master Multiplication

Here are some tips that will come in handy while multiplying:

• Memorizing tables: Multiplication is all a game of tables. So, if you have tables at your fingertips, you will find little easy to multiply.
• Making good use of the properties: If you are thorough with the properties of multiplication, you will be able to deconstruct complex problems into simpler ones. For example: 
• $3 \times 13 = 3 \times (10 + 3) = (3 \times 10) + (3 \times 3)$ (Distributive property)

This also helps in deriving new facts from the known facts. 

For example :

• If you know $2 \times 9 $ is $18$, using the commutative property of multiplication, you also know that $9 \times 2$ is also $18$.
• If you know $2 \times 10$ is $20$ and $2 \times 4 $ is $ 8$, using the distributive property of multiplication, you also know that $2 \times 14$ is $ 28$.

Fun Facts

• If you multiply any number by $1$, the answer will be the number itself. One is called the identity element under multiplication.
• If you multiply any number by zero, the result is always zero.

Conclusion

Multiplication is not just an arithmetic tool. It is a life skill that students must master at a very early age to solve real life problems.  We hope this helped you deepen your understanding of the subject.To read more such informative articles on other concepts, do visit our website. We, at Splashlearn, are on a mission to make learning fun and interactive for all students.

Solved Examples

1.  Multiply $4 \times 2$ using a number line.

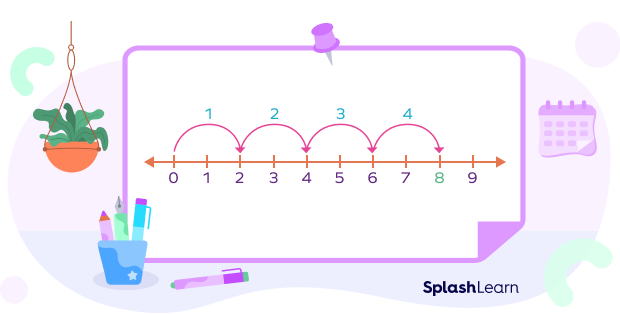
$4 × 2$ means $4$ jumps of $2$ or $2$ jumps of $4$ which is $8$ in both cases. 

1.  Compute the problem: $2 \times 16$.

$2 \times 16 = 2 \times (10 + 6) = (2 \times 10) + (2 \times 6)  = 20 + 12 = 32$.

2. $3 \times 25 = 25 \times 3$. Which property is this?

The property given above is the commutative property of multiplication i.e. $a \times b = b \times a$. 

  IV. What should we multiply to $(-$ $24)$ to get the product as $48$?

Let the number be x.

$(-$ $24) \times \times = 48$

$x = -$ $2$

   V. Multiply $\frac{2}{5}$ and $\frac{15}{8}$.

$\frac{2}{5} \times \frac{15}{8} = \frac{3}{4}$

Practice Problems

Frequently Asked Questions