Multiplier in Math – Definition, Examples, Practice Problems, FAQs

Multiplier: Introduction

A multiplier plays an important role in the basic arithmetic operation of multiplication, and so does a multiplicand, as shown in the images below. But what exactly is a multiplier? How can we identify it along with the multiplicand and use it to find a product? To know the answers to these questions, read on! 

Multiplier: Definition

A multiplier is a factor that amplifies or increases the base value of something else. 

For example, in the multiplication statement $3 \times 4 = 12$, the multiplier 3 amplifies the value of 4 to 12.

But it need not be the case always. 

• If the multiplier is 1, the value of the multiplicand remains the same in the product. For example: $1 \times 4 = 4$.
• If the multiplier is 0, the value of the multiplicand gets reduced to zero in the product. For example: $0 \times 4 = 0$.

In case of the vertical multiplication, the multiplier is the number on the top.

In case of the horizontal multiplication, the multiplier is the leftmost number.

What Is a Multiplier and Multiplicand?

Multiplication is one of the four basic operations of arithmetic. It is the result of combining groups of equal sizes. Multiplication is usually represented by the cross sign (×).

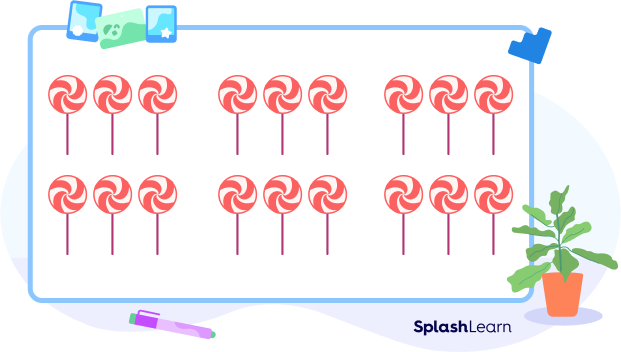
Here, each group has 6 candies, and there are 3 such groups. So, there are 3 times 6 or $6 + 6 + 6$ or 18 candies in total. 

Numerically, we can also write 3 times 6 as $3 \times 6 = 18$.

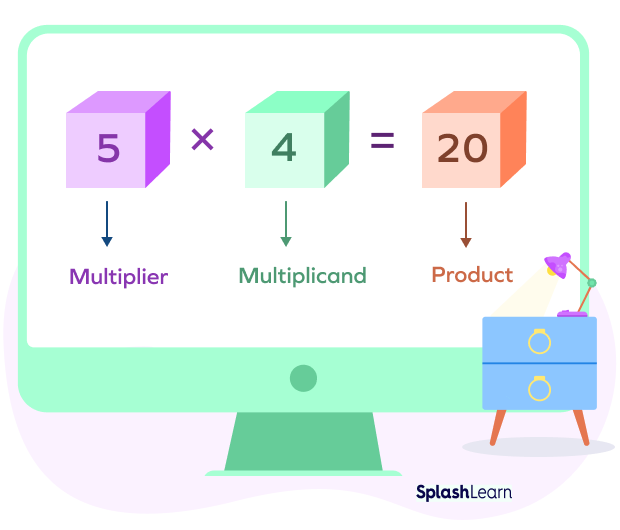
The number of objects in each group is called multiplicand. The number of such equal groups is called the multiplier.

Finally, the result of the multiplication of two numbers is called the product.

How to Find the Multiplier

To understand this concept, let’s consider a few examples:

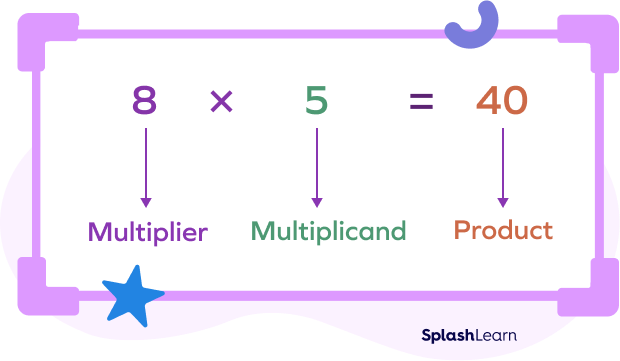
In the horizontal way of writing a multiplication statement, the multiplier is the leftmost number.

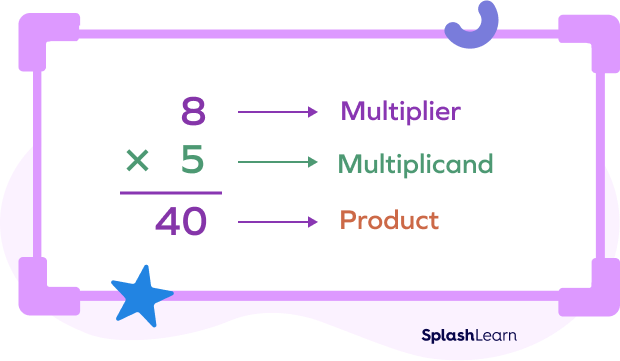
In the vertical column method of multiplication, the multiplier is the number on top.

When we represent multiplication on a number line, the multiplier is the number of jumps it takes to reach the product.

For example: $3 \times 4 = 12$

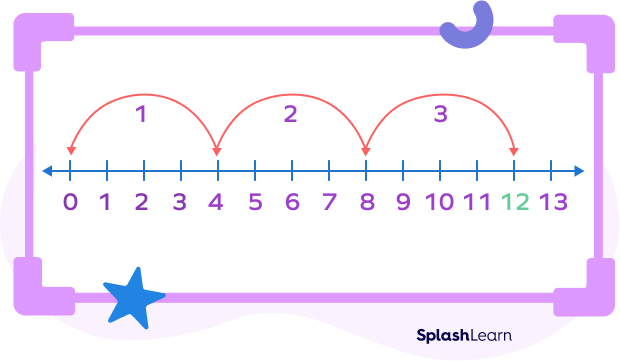
How to Find the Product Using a Multiplier

There are two ways to find the product using a multiplier. Let’s understand them with an example.

$5 \times 6 =$ ?

Here, 5 is the multiplier, and 6 is the multiplicand.

One Way: Adding the multiplicand according to the number of the multiplier. 

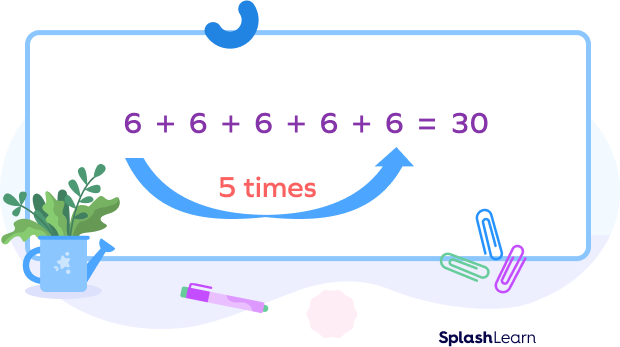
Another Way: Simply multiplying the multiplier with the multiplicand. 

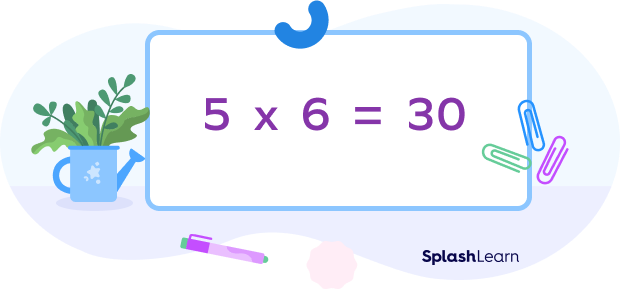
To find the product following this way, we need to keep in mind multiplication tables.

Fun Facts!

When we multiply two numbers, the order does not matter. That is: $2 \times 3 = 3 \times 2$. $2 \times 3 = 3 + 3 = 6$ $3 \times 2 = 2 + 2 + 2 = 6$ Thus, when we change the order in which the numbers are multiplied, the multiplicand and multiplier get interchanged.

Conclusion

A multiplier in math is the number by which a multiplicand (another number) is multiplied. It is usually the topmost number in the column method and the leftmost number in the horizontal multiplication method.

A multiplier, along with a multiplicand, helps in finding the product either through repeated addition or multiplication. Both are used to find the product of whole numbers, fractions, decimals, and many other numbers.

Solved Examples on Multiplier

1. Lisa has to solve $7 \times 9$. She wants to know what the multiplier and multiplicand are in this question. Help her by telling her the answer according to the horizontal method of multiplication.

Solution: In $7 \times 9$, according to the horizontal method of multiplication:

• 7 is the multiplier (the leftmost number)
• 9 is the multiplicand

2. Find $25 \times 5$.

Solution: To find the product, we need to multiply the multiplier with the multiplicand.

$25 \times 5 = 125$. 

3. Determine $6 \times 8$ using repeated addition.

Solution: To find the product using repeated addition, we need to add the multiplicand (8) according to the number of the multiplier (6).

$8 + 8 + 8 + 8 + 8 + 8 = 48$.

4. Using the column method of multiplication, Shay has to solve $15 \times 30$. 

What will be the multiplier and multiplxicand in this question?

Solution: According to the column multiplication method, we can write the question as:

    $15 \times 30$

Here, the multiplier (topmost number) is 15, and the multiplicand is 30. 

5. Find $1 \times 99$. Does the product amplify the value of the multiplicand?

Solution: $1 \times 99 = 99$.Since the multiplier is 1, the value of the multiplicand will not get amplified and remains the same upon finding the product. 

Practice Problems on Multiplier

Frequently Asked Questions on Multiplier