
Let’s say you have 12 donuts and want to distribute them equally among your three friends. How do you decide fairly how much each gets?
You just divide the donuts equally among your friends! This method of distributing a group of things into equal parts is termed as division. It is one of the four basic operations of arithmetic, which gives a fair result of sharing.
What is Division in Math?
Division is the opposite of multiplication. If 3 groups of 4 make 12 in multiplication, 12 divided into 3 equal groups give 4 in each group in division.
The main goal of dividing is to see how many equal groups are formed or how many are in each group when sharing fairly.
In the above example, to divide 12 donuts into 3 similar groups, you will have to put 4 donuts in each group. So, 12 divided by 3 will give the result 4.
Recommended Games
Mathematical Notation for Division

There are various signs that can be used to indicate division, such as
- ÷
- /
For example:
- 27 ÷ 3
- 27/3
Recommended Worksheets
Special Names for Numbers in Division Equation

Each part involved in a division equation has a special name.
Dividend: The dividend is the number that is being divided in the division process.
Divisor: The number by which the dividend is being divided by is called the divisor.
Quotient: The quotient is a result obtained in the division process.
Remainder: Sometimes, we cannot divide things exactly. There may be a leftover number. That leftover number is called the remainder.
The relationship between these four parts can be expressed as follows:
Dividend = Divisor x Quotient + Remainder
This is also called the division formula to check whether the answer is correct or not.
For example, let’s divide 16 by 3. The leftover will be 1.
Here, dividend = 16, divisor = 3, quotient = 5 and remainder = 1
So, 16 = 3 × 5 + 1
Properties of Division

To understand division better, let’s look at a few general division rules and properties:
1. If we divide a whole number (except zero) by itself, the quotient or the answer is always 1.
For example:
· 7 ÷ 7 = 1
· 25 ÷ 25 = 1
2. If we divide a whole number by zero, the answer will be undefined.
For example:
6 ÷ 0 = undefined
325 ÷ 0 = undefined
3. Zero divided by any number will give the answer zero.
For example:
0 ÷ 5 = 0
0 ÷ 100 = 0
4. If we divide a whole number (other than zero) by 1, the answer will be the number itself.
For example:
4 ÷ 1 = 4
11 ÷ 1 = 11
5. If a whole number is divided by another whole number, the quotient may not necessarily be a whole number.
For example:
15 ÷ 2 = 7.5
20 ÷ 3 = 6.67
6. In the case of exact division (with no remainder), the divisor multiplied by the quotient is the dividend. This property holds true only if all three numbers are non-zero whole numbers.
For example:
If 30 ÷ 5 = 6 then 5 × 6 = 30
7. If there are three non-zero whole numbers a, b and c, and b × c = a, then,
a ÷ b = c and a ÷ c = b
For example:
5 × 10 = 50, then,
· 50 ÷ 5 = 10
· 50÷ 10 = 5
Long Division
In math, long division is the mathematical method for dividing large numbers into smaller groups or parts. It helps in breaking down a problem into simple and easy steps.
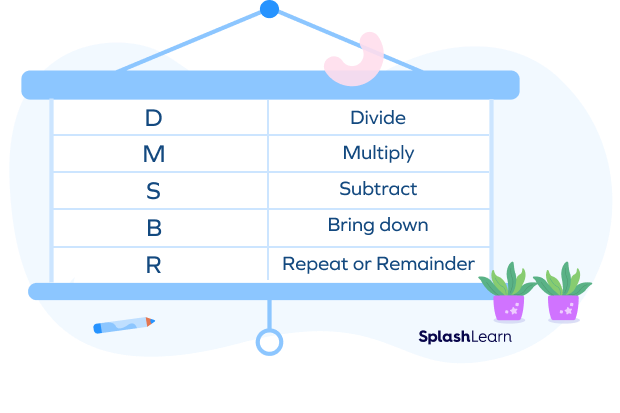
Long Division Steps
Every long division can be solved with the five steps given below.
Here’s an example that will help you understand the division steps.
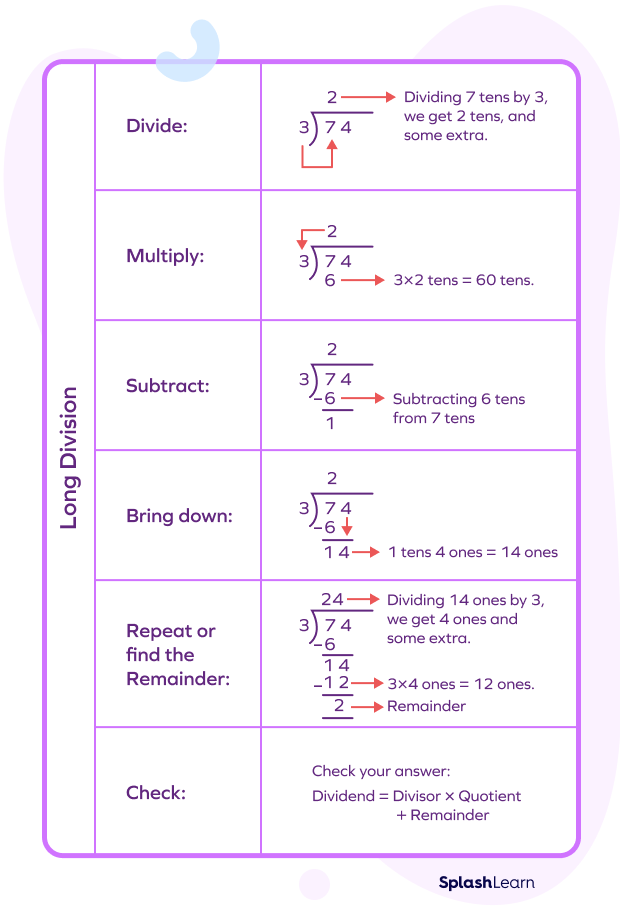
Let’s do some division examples to practice the long division steps.
Solved Examples On Division
1. Divide 171 by 3.
Solution:
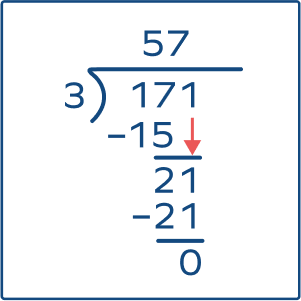
So, Quotient = 57, Remainder = 0
(Note: The writer has created the images for all the long division calculations themselves)
2. Divide 6148 by 4.
Solution:

So, Quotient = 1537, Remainder = 0
3. Divide 1579 by 6.
Solution:
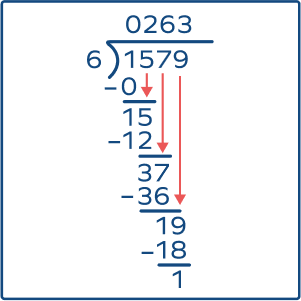
So, Quotient = 263, Remainder = 1
Practice Problems On Division
Division - Definition with Examples
Divide 1723 by 5 and find the quotient (Q) and the remainder (R).
The quotient (integer division) of $1723/5$ equals 344; the remainder (“left over”) is 3. 1723 is the dividend, and 5 is the divisor.
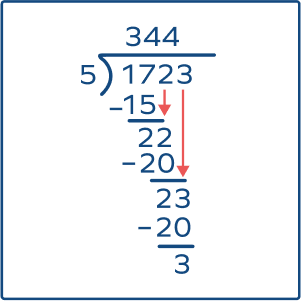
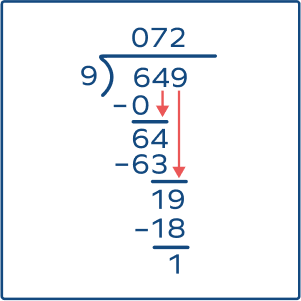
649 people are invited to a wedding party. The caterer is arranging the tables for the event. If each table has 9 seats, how many tables will be needed?
Here, the remainder is 1. So, if the caterer arranges 72 tables, 1 person will not be able to have a seat for the wedding. Hence, they will have to arrange 73 tables.
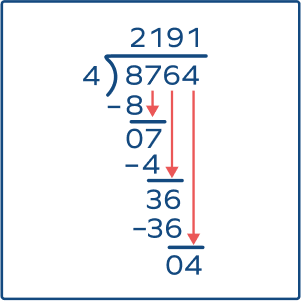
If $\$$8764 is divided equally among four people, how much will each person get?
Therefore, each person will get $\$$2191.
Harry earned $\$$20,752 in 8 months. How much money did he earn each month?
Hence, Harry earned $\$$2594 each month.

Frequently Asked Questions On Division
Does commutative property hold true for division?
Commutative property tells us that if we can move or swap numbers from their position while performing mathematical operations, the answer will still remain the same.
This property holds true for multiplication and addition but not for division.
For example: 27 × 3 = 3 × 27 but 27 ÷3 ≠ 3 ÷ 27
Can division be done through repeated subtraction?
Yes, repeated subtraction is the continuous subtraction of the same number from a large number until you get a remainder 0 or less than the actual number. Division is the shortcut to this process.
Is there a way to check the quotient and remainder in a division problem?
Yes, you can check the quotient and remainder by using the relationship:
Dividend = Divisor x Quotient + Remainder




































