Remainder –  Definition, Parts, Formula, Example

What Is a Remainder in Math?

A remainder is something which is “left over” or “remaining.” 

So, What does remainder mean in a division problem? The meaning of remainder is the leftover value or the remaining part after a division problem is called a remainder. 

In a division problem, there are two cases.

• When a number is completely divisible by another number: In this case, we are not left with anything at the end of the division.
  
• When a number is not divisible by another number: In this case, we are left with some value at the end of the division. We call it the “remainder” of the division.

Definition of Remainder

The definition of remainder in math can be given as the leftover number in a division problem. If the number is not completely divisible by another number, then we are left with a value, which is called remainder. A remainder is always less than the divisor.

Parts of a Division

The four important parts of any division problem are:

• Dividend
• Divisor
• Quotient
• Remainder

In a division problem, the number that is being divided is called dividend. The number that divides the dividend is called divisor. The result of the division is called a “quotient.” When the dividend is not completely divided by the divisor, the leftover value is called “remainder.”

Example: Divide 25 by 6. 

We know that $6\times4 = 24$

Thus, quotient $= 4$ and we are left with the remainder of 1.

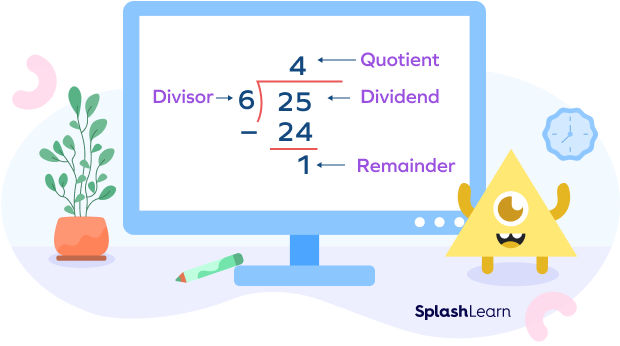
We can write this as $25 \div 6 \rightarrow 4 R 1$, where 4 is the quotient and 1 is the remainder.

Remainder in Division: Examples

Let’s discuss a few examples.

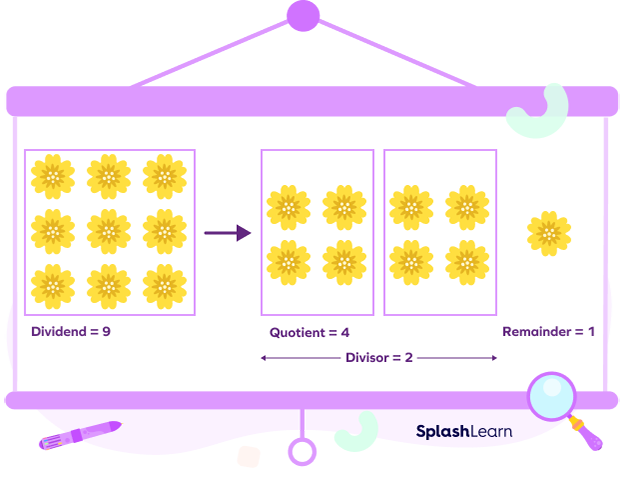
Example 1: Suppose you have 9 flowers (9 is the dividend). You wish to divide the flowers equally into 2 groups (2 is the divisor). Each group will have 4 flowers (4 is the quotient). Thus, 8 flowers get distributed equally and 1 flower is left over. 

Example 2: The number 16 is not exactly divided by 5. The closest value to 16 that we can get is $5\times3 = 15$

Therefore, $16 \div 5$ gives the quotient 3 and the remainder is $16\;-\;(5\times3)= 1$

Hence, $R = 1$

Example 3: Division problem with remainder 0.

$27\div9 = 3$

27 is completely divisible by 3. Thus, the remainder is 0.

Remainder Formula

In a division problem, the dividend, divisor, quotient and remainder are related by the following equation 

$Dividend = (Divisor \times Quotient) + Remainder$

Thus, we can express the remainder as

$Remainder = Dividend\;-\;(Divisor \times Quotient)$

How to Find the Remainder

How to find a remainder in a division problem? Let’s understand the steps with an example. This method is convenient to use when the numbers involved are small and easy to use for calculations.

Example: Find the remainder when 69 is divided by 6.

Step 1: Identify the parts of the division. 

Here, dividend $= 69$, divisor $= 6$

Step 2: Check if the dividend appears in the table of the divisor. If not, find the multiple of the divisor nearest to the dividend.

Here, 69 is not in the table of 6. It is not completely divisible by 6.

Nearest multiple of $6 = 6\times11 = 66$

and quotient $= 6$

Step 3: Subtract this multiple from the dividend.

$69\;-\;66 = 3$

You can also use the formula we discussed earlier. 

$Remainder = Dividend\;-\;(Divisor \times Quotient)$

Here, remainder $= 69 – (6\times11) = 3$

$18 \div 7$	Quotient $= 2$	Remainder $= 4$
$15 \div 10$	Quotient $= 1$	Remainder $= 5$
$23 \div 6$	Quotient $= 3$	Remainder $= 5$
$46 \div 9$	Quotient $= 5$	Remainder $= 1$
$15 \div 5$	Quotient $= 3$	Remainder $= 0$

Long Division Method

The best way to find the remainder is the long division method. When the dividend is a large number, it is better to use the long division method. It is a method for dividing large numbers into smaller groups or parts. It helps to break down a problem into simple and easy steps.

Note that the remainder always has to be less than the divisor. If it is more than the divisor, it means the long division is incomplete.

Example: Divide 75 by 4. Find the remainder.

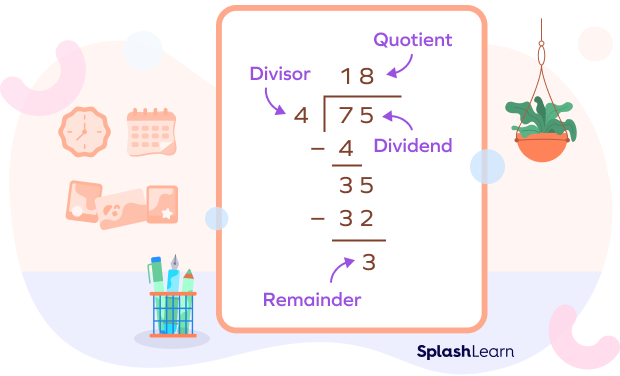
Properties of a Remainder

• A remainder is always less than the divisor. 
• If one number (divisor) divides the other number (dividend) completely, then the remainder is 0. It is referred to as a complete division.
• If a dividend is a multiple of the divisor, then the remainder is 0.

Learn About Remainder with an Activity

Long division is a method that allows us to divide large numbers into multiple smaller groups or parts. When we divide a dividend with a divisor, the quotient obtained is the number of groups that can be made, and the remainder identifies how many elements or numbers that will be left ungrouped. 

Let’s do a fun activity and understand both division and remainder concepts.

Consider a group of objects that needs to be divided into equal groups. 

• Number of objects: Dividend
• Number of groups: Divisor
• Number of items in each small group: Quotient
• Number of items left: Remainder

Example 1: How can we divide 12 flowers among 3 children?

When 12 flowers are divided among 3 children, each child will get 4 flowers and no flower will be left.

Example 2: Divide 9 books into 2 equal groups. How many books are left?

When 9 books are divided among two groups each group gets 4 books and 1 book is left.

When we cannot make equal groups or distribute equally to all the groups, the number that is left undivided is called the remainder. 

How to Represent the Remainder

We can represent the parts of the division problem using a single equation.

Example 1: If you have 9 toffees and you share it equally with your four friends. How many toffees will you have? 

If you give two toffees each to your friends, you would have shared 8 toffees. Only 1 toffee will remain with you, and this leftover of 1 toffee is called the remainder.

Mathematically, we can write the above expression as:

$9 \div 4 = 2 \;R\; 1$

9 is the dividend, 4 is the divisor, 2 is the quotient, and 1 is the remainder.

Example 2: Divide 22 by 3. 

We get 3 equal parts of 7 that add up to 21.

$3\times7 = 21$

We are left with 1. This 1 is the remainder.

We represent this as: $21 \div 7 = 3$

Example 3: Another way to represent the remainder is by representing in the form of mixed fractions. The number 19 divided by 2 can be written as $\frac{19}{2} = 9\frac{1}{2}$.          

Facts about Remainder

• When one number divides another number completely, the remainder is 0 and the division is called complete division.

• The word remainder comes from the Latin word “remanere,” which means “to remain.”

Conclusion

In this article, we learned about remainder in a division problem, methods of finding remainder, the long division method, properties of a remainder. Let’s solve a few examples to understand the concept better.

Solved Examples on Remainder

1. Find the remainder when 23 is divided by 4.

Solution:

Here, divisor $= 4$, dividend $= 23$  

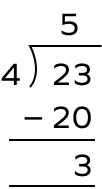
Remainder $= 3$

 2. Find the remainder when 87 is divided by 3.

Solution:

Here, divisor $= 3$, dividend $= 87$  

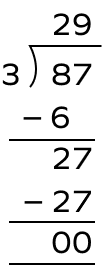
87 is completely divisible by 3. Thus, the remainder is 0.

3.  What is the missing term?

Solution:

Here, the divisor is 7 and the dividend is 456. 

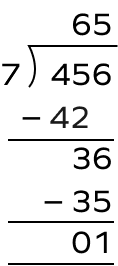
The missing term $= 7\times6 = 42$

4. Find the dividend, divisor, quotient, and remainder, when 100 is divided by 9?

Solution:

Here, divisor $= 9$ and dividend $= 100$ 

The multiple of 9 nearest to $100 = 9\times11 = 99$

Thus, quotient $= 11$

Remainder $= 100\;-\;99 = 1$

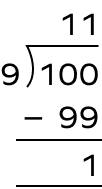
Practice Problems on Remainder

Frequently Asked Questions on Remainder