What Is a Divisor in Math?
In division, the divisor is the number by which the dividend is divided to obtain the quotient.
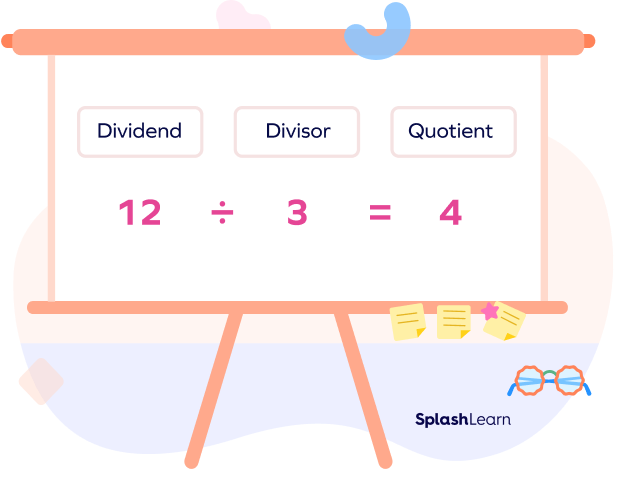
A number that divides another number either completely or partially is known as a divisor. In other words, a divisor in a division problem is a number we divide another number by.
Divisor Examples:

What is Division?
Division is a mathematical operation that involves splitting a quantity or number into equal parts or groups.
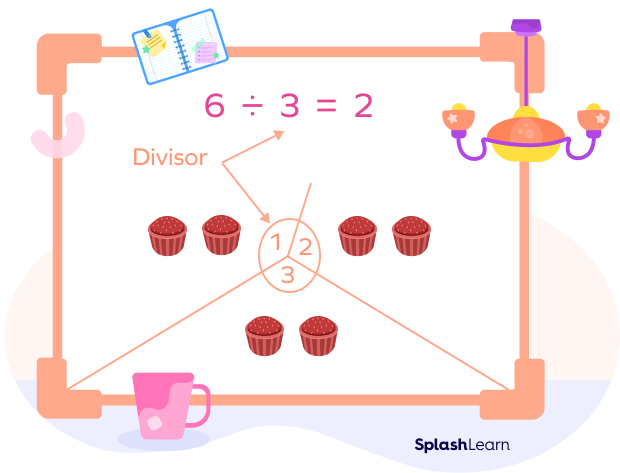
Example: Divide 20 balls equally into five boxes.
This is defined by a division problem: $20 \div 5$
$20 \div 5 = 4$
Each box gets 4 balls.

Recommended Games
Dividend, Divisor, Quotient, and Remainder
Four important parts in any division problem are:
Dividend, Divisor, Quotient and Remainder.
- Dividend is the number or quantity being divided.
- Divisor is the number by which we divide the dividend.
- Quotient is the answer to the division problem. It is the number which we get by dividing a number.
- Remainder is the number which is left after dividing the two numbers.
Example 1:
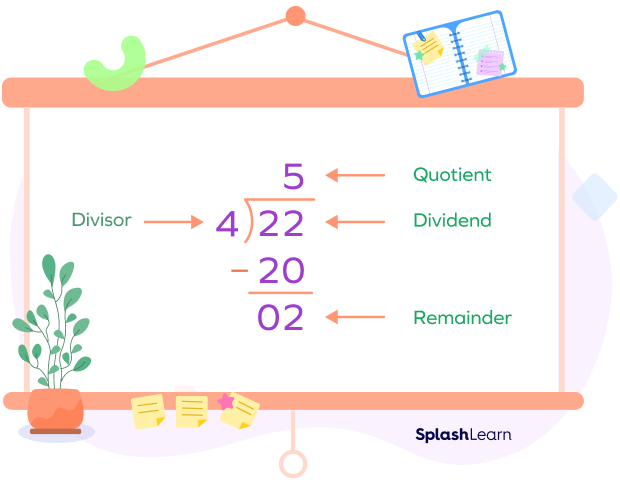
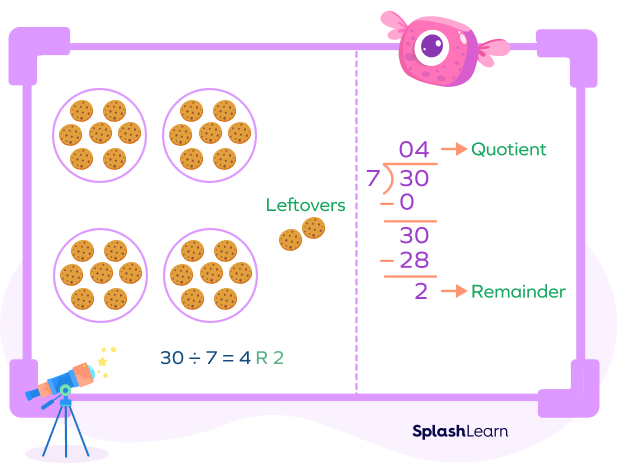
Example 2: $30 \div 7$
Dividend $= 30$
Divisor $= 7$
Quotient $= 4$
Remainder $= 2$
Recommended Worksheets
How to Identify the Divisor
Identifying a divisor is quite simple. It is the number by which a given number (dividend) is divided.
Example: If we divide the number 45 by 9, it can be represented as $45 \div 9$.
Here, 45 is the dividend.
We are dividing 45 by 9.
Thus, 9 is the divisor.
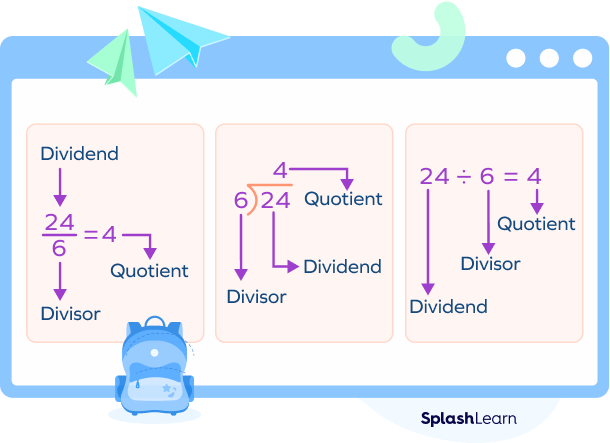
There are different ways to write a division problem. Let’s understand the different parts of the division in each case.
What Does the Divisor Represent in a Division?
As mentioned earlier, in the division problem, we break a large number into equal groups.
Divisor is the quantity that determines the number of equal parts or groups the dividend is divided into. The divisor indicates the size or magnitude of each part or group.
Divisor Formula
The relationship between the dividend, divisor, quotient and remainder is given by
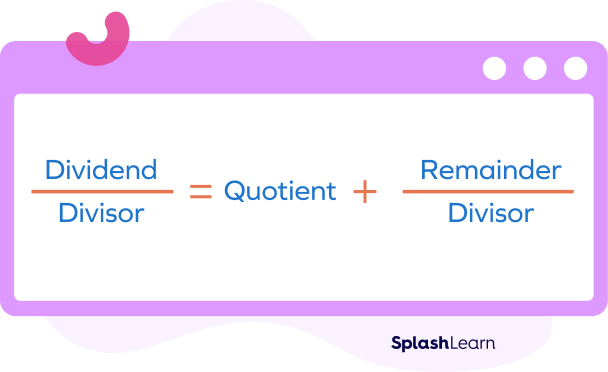
We can also write this as
Dividend = (Divisor × Quotient) + Remainder
Using this equation, we can define the divisor formula.
Let’s discuss two situations – with or without a remainder:
| When remainder = 0 | When remainder 0 |
| Divisor = Dividend ÷ Quotient | Divisor = (Dividend – Remainder) ÷ Quotient |
Properties of Divisor
1) Zero cannot be a divisor.
2) When the divisor is 1, the quotient equals the dividend.
3) When the dividend is the same as the quotient, the divisor = 1.
Example: 65 ÷ 1 = 65.
4) When the dividend equals the divisor, then the quotient = 1.
Example: 65 ÷ 65 = 1.
5) The remainder is always less than the divisor.
Difference between Divisors and Factors
In a division problem, the term ‘divisor’ refers to the number that divides the dividend. It does not matter if the remainder is zero or non-zero.
A factor is a positive integer that divides a given number exactly, leaving no remainder. Thus, if the divisor evenly divides the dividend with 0 remainder, the divisor is termed as the factor of that particular number.
A factor of any number is a special case where the remainder of division is 0.
NOTE: You might notice that the terms ‘divisor’ and ‘factor’ are often used interchangeably. Understanding the context is very important to avoid confusion and misunderstanding.
Examples:
- The divisors of 6 are 1, 2, 3, and 6. It means that the numbers 1, 2, 3, and 6 evenly divide the number 6, without any remainder.
- If you divide 100 by 3, the dividend is 100 and the divisor is 3. This does not mean that 3 divides 100 evenly without remainder. 3 is not a factor of 100. Here, the term “divisor” simply explains the role of number 3 in the division problem.
Special Divisors: Division by Powers of 10
- When the divisor is 10, the decimal point will move one place to the left.
Example: $15 \div 10 = 1.5$
- When the divisor is 100, the decimal point will move two places to the left.
Example: $256 \div 100 = 2.56$
- When the divisor is 1000, the decimal point will move three places to the left.
Example: $345 \div 1000 = 0.345$

Facts about Divisor
- When the divisor is greater than the dividend, then the quotient will be a fraction or a decimal number which is less than 1.
- Example: $20 \div 50 = \frac{20}{50} = \frac{2}{5} = 0.4$
- A divisor can never be zero because the division by zero is undefined.
- When zero is divided by any non-zero divisor, we always get zero as the quotient.
- When dividend and divisor are both 0, the division is indeterminate.
- If the remainder is 0, that means the divisor completely divides the dividend, or the dividend is ‘divisible by’ the divisor.
Conclusion
In this article, we learned about divisors, how to identify divisors, their properties, and different parts of division. We also discussed how different powers of 10 act as special divisors. Let’s solve a few examples and practice MCQs for better comprehension.
Solved Examples on Divisor
1. Identify dividend and divisor in each division problem.
i) 108 ÷ 12
ii) 24 ÷ 5
iii) 200 ÷ 10
iv) 7 ÷ 2
Solution:
| Sr. No. | Division problem | Dividend | Divisor |
|---|---|---|---|
| i) | 108 ÷ 12 | 108 | 12 |
| ii) | 24 ÷ 5 | 24 | 5 |
| iii) | 200 ÷ 10 | 200 | 10 |
| iv) | 7 ÷ 2 | 7 | 2 |
2. Define the parts of division when 729 is divided by 9.
Solution:
729 is divided by 9.
Dividend is the number being divided.
Dividend = 729
Divisor is the number we divided the dividend by.
Divisor = 9
Let’s divide.
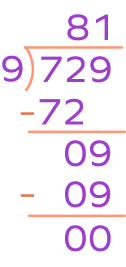
$72 \div 99 = 81$
Thus, quotient = 81
Remainder = 0
3. Alex distributed 12 strawberries equally. Everybody got only 1 strawberry. What is the divisor and what does the divisor represent?
Solution:
Number being divided = 12
Everybody got only 1 strawberry.
So, quotient = 1
Here, the divisor is the number of groups or the total number of equal parts of 12.
Since the quotient is 1, Alex actually divided 12 strawberries into 12 equal parts (friends), such that each person got 1 strawberry.

Practice Problems on Divisor
Divisor
The cost of 24 apples is equal to $120. In order to find the cost of 1 apple, what will be the divisor?
To find the cost of 1 apple, we divide $\$120$ by 24.
Thus, divisor = 24.
If the remainder is 0, which of the following is true?
When the remainder is 0, then Divisor = Dividend $\div$ Quotient
What will be the divisor if the dividend is 25 and the quotient is 0.25 and the remainder = 0?
Dividend = 25
Quotient = 0.25
Remainder = 0
When the remainder is 0, then Divisor = Dividend $\div$ Quotient
Divisor = 25 $\div$ 0.25 = 100
Which of the following is NOT a factor of 14?
Factors of 14 are: 1, 2, 7, 14.
Frequently Asked Questions On Divisor
Is a number a factor of itself?
Yes, a number is a factor of itself as a number can divide itself completely without leaving any remainder. This means that it will give the quotient as 1. Every number is the largest factor of itself.
Example: $15 \div 15 = 1$
What is the Greatest Common Divisor?
The greatest common divisor is the greatest number among the common divisors for a given set of positive integers. Example: GCD for 24 and 36 is 12.
What is the quotient?
The quotient is the result or outcome of the division operation and represents the number of times the divisor is contained within the dividend.
What is the difference between the denominator and divisor?
Denominator is the number written at the bottom in a fractions and it tells us about the total number of parts a whole is divided into. In a fraction ab, the numerator is “a” and the denominator is “b.”
Divisor is the number we divide another number by. If we denote a division problem as a/b, then “a” is the dividend and “b” is the divisor.




































