Less Than
The relationship between two quantities can be described using comparison terms. There are primarily three comparison terms: greater than (>), less than (<), and equal to (=).
Greater than (>):
When one quantity is more than the other quantity, we use “greater than”.
For example, 5 > 3.
Less than (<):
When one quantity is smaller than the other quantity, we use “less than”.
For example, 8 < 10.
Equal to (=):
When two quantities are the same, we use “equal to”.
For example, 15 = 15.
Recommended Games
Less than Definition
It is one of the terms used to show a relationship between two values. It states that one value is lesser than or lower than or fewer than or smaller than the other. The less than symbol is “<” and with this metric, we can compare numbers, weights, heights, and values.
Let’s look at some examples of less than.
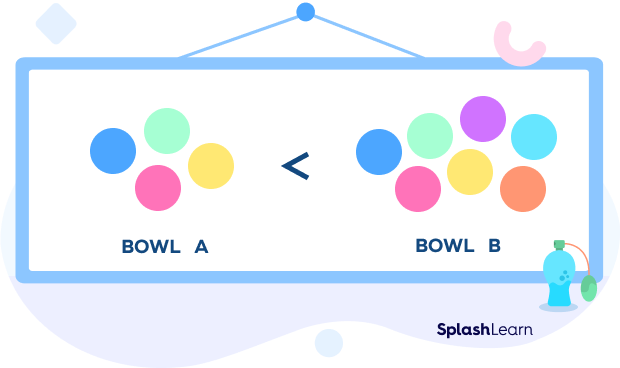
Example 1, there are 4 marbles in Bowl A, and 7 marbles in Bowl B. On comparing the two, it is clear that Bowl A has fewer marbles than Bowl B.
Weights can be compared similarly.
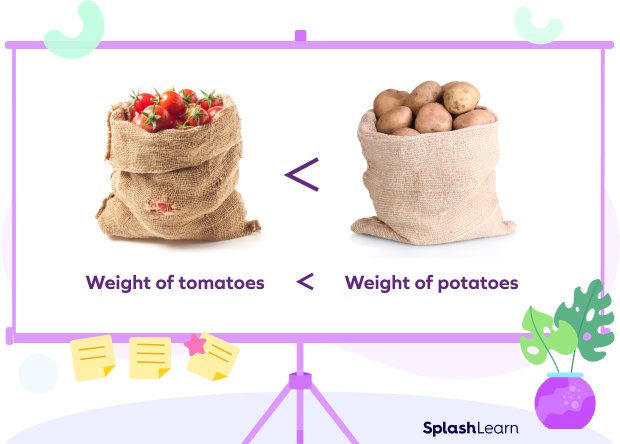
Example 2, Ray buys 8 lb of potatoes and 4 lb of tomatoes and puts them in two separate bags. He hands over the lighter bag to his son. Which one does he hold himself?
Well, for that, it is important to find out which bag is lighter. There are two bags, the one with the potatoes weighs 8 lb, and the other that has tomatoes weighs 4 lb. So, the bag of tomatoes weighs less and Ray hands it to his son, while he carries the bag of potatoes.
Example 3, John has 6 bars of chocolates. Rita has 2 bars of chocolates and Suma has 3 bars of chocolates. Does John have more chocolates than Rita and Suma combined?
The total number of bars that Rita and Suma have = 2 + 3 = 5 bars
And John has 6 bars of chocolates.
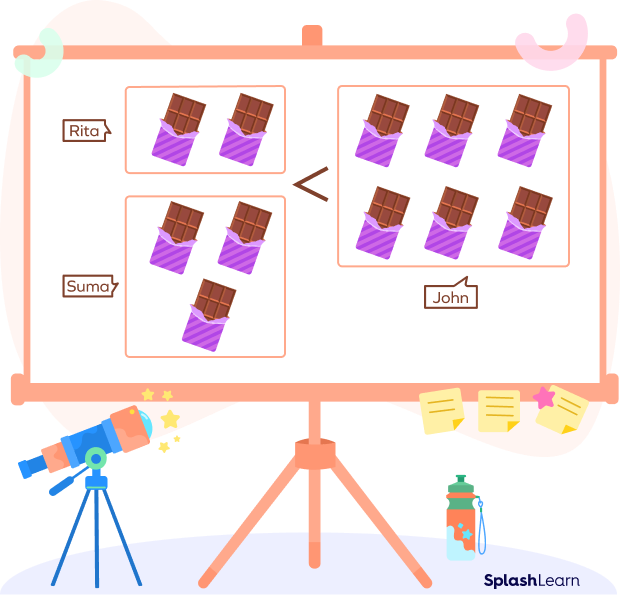
Therefore, Rita and Suma together have fewer chocolates than John.
Recommended Worksheets
Less Than on the Number Line
To show the lesser than sign on the number line, we use an empty circle to mark the limit value and point an arrow towards the given condition of inequality. The empty circle shows that a limit value is not the solution to the given inequality.
Let’s look at the steps to represent inequality of the form x < 3 on the number line.
Step 1: Locate “3” on the number line and mark it with the empty circle.

Step 2: The inequality x < 3 shows that the variable x is allowed to have any value smaller than 3, which means all the values on the left of this circle. Starting from the empty circle(limit value), extend an arrow to the left end signifying all the values the variable x can have.
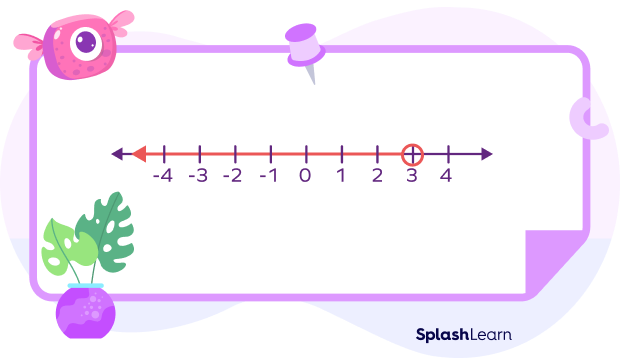
Note: If the inequality was “less than or equal to” we would have filled the circle. A filled circle shows that the limit value is also the solution to given inequality.
Difference between Comparison Symbols
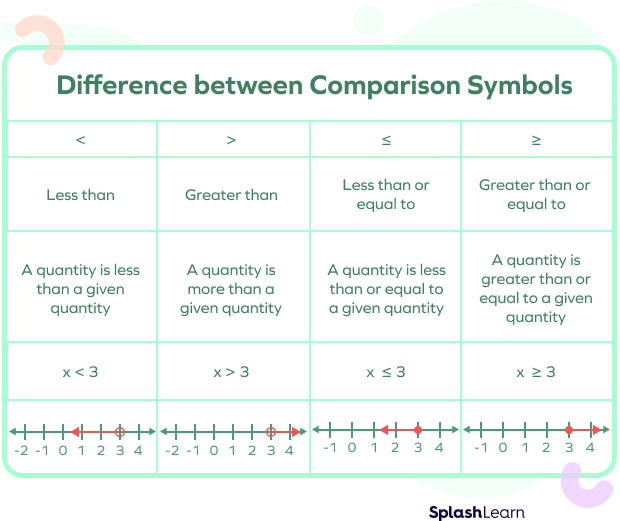
To sum up, comparison plays a significant role in our lives. Without comparison, it is difficult to show the equality or inequality between things that we see around us.
| Fun Facts British mathematician Thomas Harriot first used the sign for less than (<) in 1631, in his book Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas. |
Solved Examples
Example 1: Select the numbers that are smaller than 20 from the given set of numbers.
0, 14, 21, 20, 18, 22, 36, 45, 12, 3, 15, 99, 27
Solution:
0, 14, 18, 12, 3, 15 – are all numbers < 20.
Example 2: In an aquarium, there are various types of fish.

Which type of fish are less than 60 in number?
Solution:
Guppies (45), zebra fish (25), and tiger barb (26) are all < 60 in number.
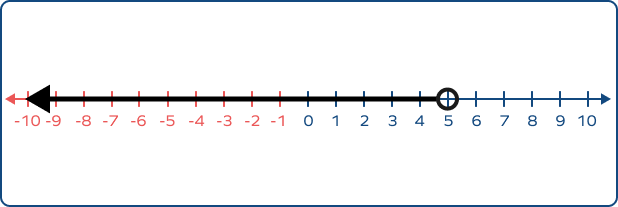
Example 3: Graph x < 5.
Solution:
Example 4: State whether true or false:
- 15 < 15
- 15 < 18
- 15 < 14
- 15 < 20
Solution:
- False
- True
- False
- True
Practice Problems
Less Than in Math - Definition with Examples
Choose the possible value that satisfies a number$\lt$10.
4$\lt$10. All other options are either greater than or equal to 10.
Choose the correct graph that best describes numbers $\lt$ 4.
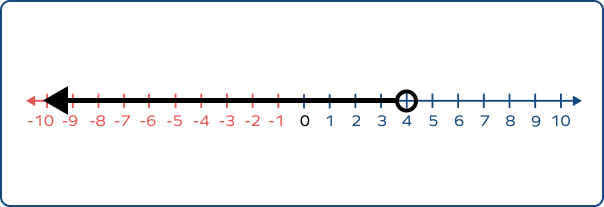
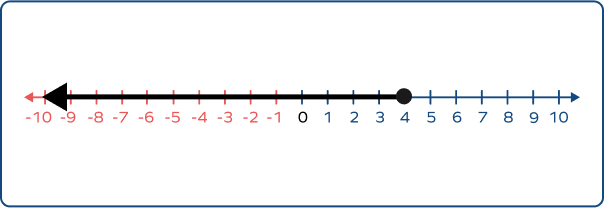
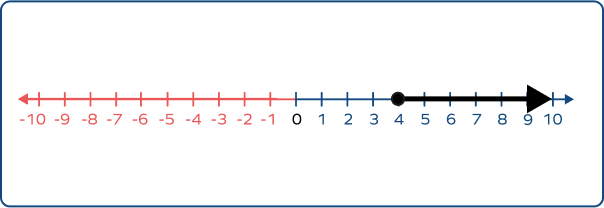
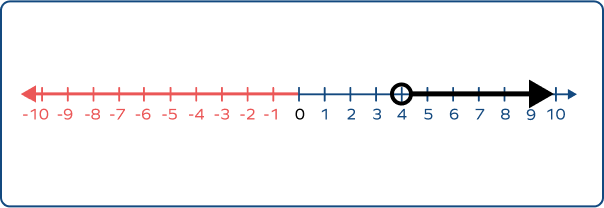
The graph of numbers $\lt$ 4 should have an empty circle marked at 4, and an arrow starting from 4 and extending to the left of it.
There are 50 apples in basket A, 42 apples in basket B, 46 apples in basket C and 44 apples in basket D. Which basket has fewer apples than Basket D?
42 (B) $\lt$ 44 (D) $\lt$ 46 (C) $\lt$ 50 (A). So, basket B has fewer apples.
Choose the statement that explains 23 $\lt$ 50.
The “$\lt$” symbol represents less than.
Frequently Asked Questions
What is the difference between less than and less than or equal to?
Less than is represented by “<” and less than or equal to is represented by “≤”. The first term means that the variable or quantity has to have a value lesser than the given limit, whereas “less than or equal to” means that the variable or quantity has to be equal to or lesser than the given limit.
What is greater than?
It shows that one quantity is greater than the other quantity. Greater than is one of the terms used to show the relationship between two values. It states that one value is greater than or more than or larger than or bigger than the other. The sign for greater than is ”>”.
Is –5 lesser than 5, and if so, what is the mathematical representation?
Yes, –5 is lesser than 5. Therefore, the mathematical representation for the given statement will be –5 < 5.
What are different inequality symbols?
Greater than (>), less than (<), not equal to (≠), greater than or equal to (≥), and less than or equal to (≤) are inequality terms and symbols.




































