Definition of Quotient
The number we obtain when we divide one number by another is the quotient.
For example, in 8 ÷ 4 = 2; here, the result of the division is 2, so it is the quotient. 8 is the dividend and 4 is the divisor.
Note that the quotient and the divisor are always smaller than their dividend.
Recommended Games
Different Forms of Quotient
The quotient can be an integer or a decimal number.
- When a number is completely divisible by another number, the quotient is a whole number.
For example, 15 ÷ 3 = 5 (whole number)
- When a number is not completely divisible by another number, the quotient is a decimal number.
For example, 15 ÷ 2 = 7.5 (decimal number)
Such divisions leave a remainder, so there is another way of writing answers to such division problems, which is:
15 ÷ 2 = 7 R 1 (where, quotient = 7 and remainder = 1)
Recommended Worksheets
Finding Quotients by Repeated Subtraction
It can be helpful to think of division as a repeated subtraction problem. To divide by repeated subtraction, we subtract the divisor from the dividend till we get a 0 or until subtraction is no longer possible. In this process, the number of times we subtract is the quotient.
Let’s find the quotient of 20 ÷ 5 using repeated subtraction.
20 – 5 = 15
15 – 5 = 10
10 – 5 = 5
5 – 5 = 0 (STOP)
We subtracted 5 four times to get a 0, so 4 is the quotient. That is, 20 ÷ 5 = 4
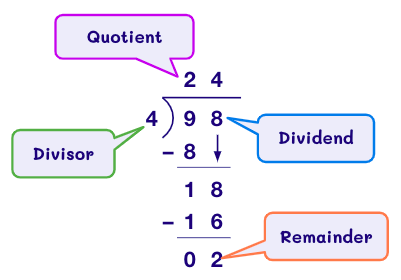
Finding Quotients by Long Division Method
In math, long division is a method used for dividing large numbers into groups or parts. To divide a number using this method, a division house is drawn. The divisor is written outside the division house, while the dividend is placed within. The quotient is written on top of it.
Long Division involves five steps:
D → Divide
M → Multiply
S → Subtract
B → Bring Down
R → Repeat/ Remainder
For example:
Solved Examples
Example 1: Find the quotient: 28 ÷ 3 using repeated subtraction.
Solution:
28 – 3 = 25
25 – 3 = 22
22 – 3 = 19
19 – 3 = 16
16 – 3 = 13
13 – 3 = 10
10 – 3 = 7
7 – 3 = 4
4 – 3 = 1 (3 cannot be subtracted from 1, so we stop here)
We subtracted 3 nine times to get , so, 4 is the quotient. That is, 20 ÷ 5 = 4
Example 2: Find the quotient 153 ÷ 7 using the long division method.
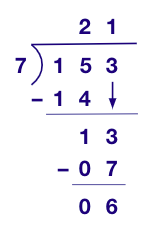
Quotient = 21; Remainder = 6
Example 3: Jack needs 2 mangoes to make a glass of mango juice. If he has 28 mangoes, how many glasses of mango juice can he make?
Solution:
Number of mangoes with Jack = 28
Number of mangoes required for 1 glass of juice = 2
Number of glasses of juice Jack can make = 28 ÷ 2
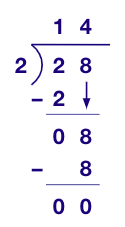
Number of glasses of juice Jack can make = 14 glasses
Practice Problems
Quotient
Find the quotient: 15 ÷ 3.
We know that, 3 ✕ 5 = 15, so, 15 ÷ 3 = 5.
Find the quotient: 90 ÷ 3.
We know that, 30 ✕ 3= 90, so, 90 ÷ 3 = 5.
Find the quotient 400 ÷ 10.
We know that, 40 ✕ 10 = 400, so, 400 ÷ 10 = 40.
Frequently Asked Questions
What Is the difference between quotient and product?
Quotient is the result of dividing two numbers and product is the result of multiplying two numbers.
What are the different terms related to division?
Dividend → the number to be divided
Divisor → the number by which a dividend is divided
Quotient → the result of dividing the dividend by the divisor
Remainder → the number leftover after division
What is the difference between a quotient and a remainder?
The leftover part after division is known as the remainder while the quotient is the number we obtain when we divide one number by another. For perfect divisions, a quotient is a whole number, and the remainder is zero. In general, a remainder is sometimes accounted into the quotient, making it a decimal number.
How Can We Verify the Quotient in Division?
Dividend = Divisor × Quotient + Remainder




































