Subtraction: Introduction
Suppose we purchase ice cream for a certain amount of money, say $\$140$, and we give $\$200$ to the cashier. Now, the cashier returns the excess amount by performing subtraction such as $200 − 140 = 60$. Then, the cashier will return $\$60$.
What is exactly happening here?
The answer to this question is subtraction.
Recommended Games
What is Subtraction in Math?
Subtraction is one of the four basic arithmetic operations in mathematics. The other three being addition, multiplication, and division.
We can observe the applications of subtraction in our day-to-day life in different situations.
For example, if we have 3 candies and our friend asks us for 1 candy, how many candies are we left with? Simply,
$3 − 1 = 2$
Let’s understand the concept with the help of the following example of apples.

In the example above, if Harry has 6 apples and he gives 3 apples to Jim, How many apples are left with him?
We can calculate this by subtracting 3 from 6:
$6 − 3 = 3$
Harry is left with 3 apples.
Recommended Worksheets
Definition of Subtraction
The operation or process of finding the difference between two numbers or quantities is known as subtraction. To subtract a number from another number is also referred to as ‘taking away one number from another’. Some instances where we use subtraction are while making payments, transferring money to our friends and many more.
Symbol of Subtraction
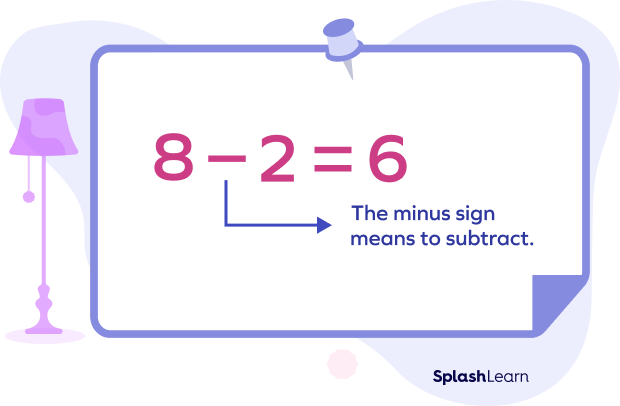
In mathematics, we have generally used different symbols for different operators. We have symbols like $+, −, /, *$ and many more. The subtraction symbol $“−”$ is one of the most important math symbols that we use. In the above section, we read about subtracting two numbers 6 and 3. If we observe this expression: $(6 − 3 = 3)$, the symbol $(−)$ between the two numbers is what denotes subtraction. This symbol is also known as the minus $(−)$ sign.
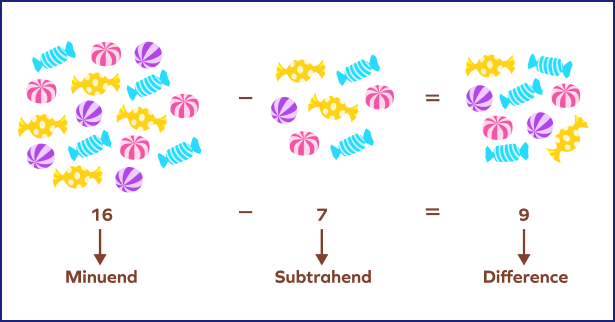
Formula of Subtraction Operation
When we subtract two numbers, we commonly use some terms that are used in a subtraction expression:
Minuend: A minuend is the number from which the other number is subtracted.
Subtrahend: A subtrahend is the number which is to be subtracted from the minuend.
Difference: A difference is the final result after subtracting the subtrahend from the minuend.
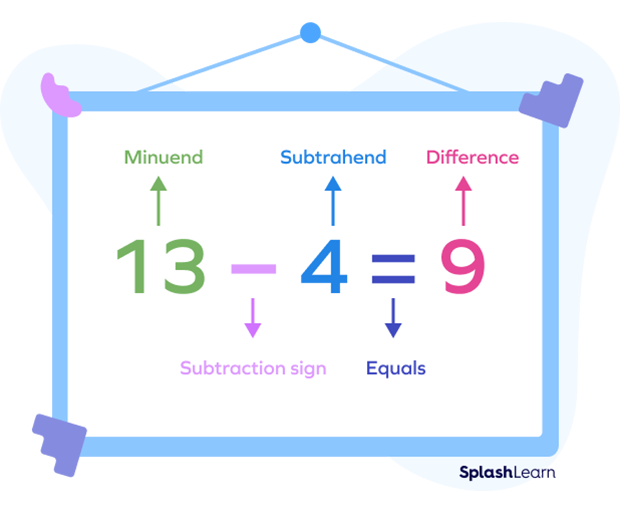
The subtraction formula is written as
Minuend $−$ Subtrahend $=$ Difference
For example,
$7 − 3 = 4$
Here,
$7 =$ Minuend
$3 =$ Subtrahend
$4 =$ Difference
What Is Minus in Math?
Minus is a sign or a symbol that is represented by a horizontal line.

We use minus in mathematics for multiple representations.
Uses of Minus Sign
Subtraction Operation
Minus represents the arithmetic operation of subtraction between two numbers. We use minus sign to denote subtract, decreased by, take away, etc.
For example,
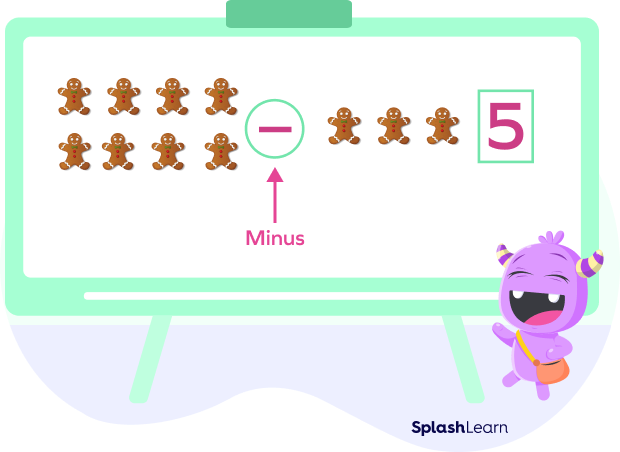
Minus sign also means how much is one value more than the other value.
For example, Darby has 8 gingerbread with her and Olive has 3 gingerbreads.
Darby has more gingerbreads by $(8 − 3) = 5$
To Represent Negative Integers
Integers are the numbers that are not in decimal or fractional form and include positive and negative numbers along with 0. We use the minus sign to represent the negative integers, i.e., the whole numbers which are less than zero (no fractions).
For representing a negative integer, we add a negative or minus sign in front of a whole number. For example, negative integer 5 is represented as: $(− 5)$
Use in Measurement
We also use the minus sign in measurement specially in temperature.
For example, a temperature of $− 4^{\circ} \text{C}$ means 4 degrees below zero.
Another example: The temperature is $5^{\circ} \text{C}$ and then drops $− 10^{\circ} \text{C}$. What is the temperature now?
The temperature now $= 5 − 10 = − 5^{\circ} \text{C}$

To Represent Opposite Directions
We also use the minus sign to represent a negative direction on a graph paper to show the coordinates.
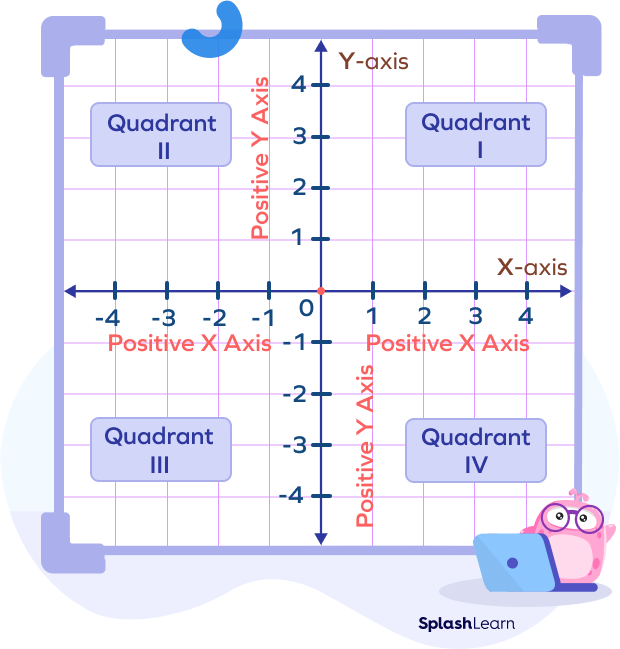
The graph also runs in the negative direction.
- In the first quadrant, the coordinates are of the form $(x,y)$.
- In the second quadrant, the coordinates are of the form $(−x,y)$.
- In the third quadrant, the coordinates are of the form $(−x,−y)$.
- In the fourth quadrant, the coordinates are of the form $(x,−y)$.
Mathematical Operations on Integers Using “Minus” Sign
- Multiplication of two negative numbers gives a positive number.
Negative $\times$ Negative $=$ Positive
For example, $(− 5) \times (− 15) = + 75$
- Multiplication of a negative number and a positive number gives a negative number.
Negative $\times$ Positive $=$ Negative
For example, $(− 5) \times (15) = − 75$
- Addition of a negative number with a negative number will always give a negative number.
Negative $+$ Negative $=$ Negative
For example, $(− 3) + (− 4) = (− 7)$
- Subtracting a positive number from a negative number will always give a negative number.
If we subtract a positive number from a negative number, we start at the negative number and count backwards.
Negative $−$ Positive $=$ Negative
Using the number line, let’s start at $− 3$.
For example: Say, we have the problem $(− 2) − 3$.
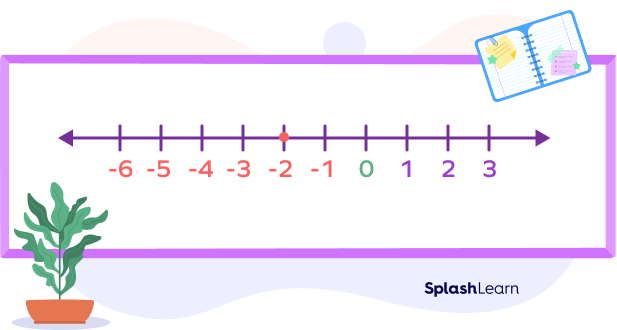
Now count backwards 3 units. So, keep counting back three spaces from $− 2$ on the number line, we get
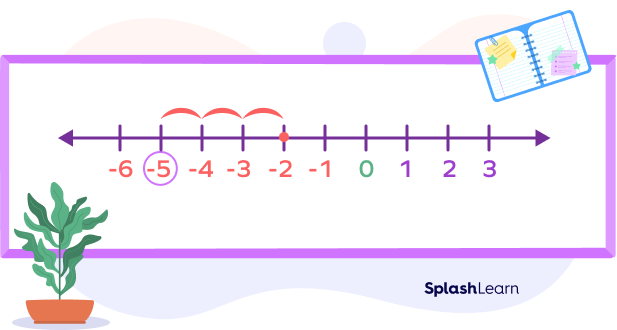
The answer is $(− 2) − 3 = − 5$.
- Subtracting a negative number from a negative number
A negative sign followed by a negative sign, turns the two signs into a positive sign. So, instead of subtracting a negative, you are adding a positive. The answer could be either positive or negative, depending on the magnitude of the numbers.
Negative $−$ Negative $=$ Negative $+$ Positive
Basically, $− (− 5)$ becomes $+ 5$, and then you add the numbers.
For example, we have $(− 2) − (− 5)$. We can read it as “negative two minus negative 5”. We’re changing the two negative signs into a positive, so the equation now becomes $(− 2) + 5$.
On the number line, it starts at $− 2$.
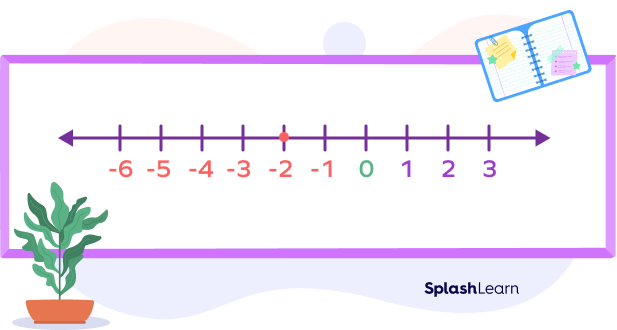
Then we move forward 5 units: $+ 5$.
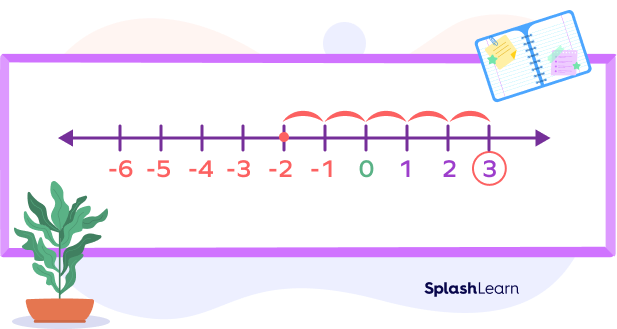
The answer is $− 2 − (− 5) = 3$.
- Subtracting a negative number from a positive number will always give a positive number.
When we subtract a negative number from a positive number, we turn the subtraction sign followed by a negative sign into a plus sign. So, instead of subtracting a negative, you’re adding a positive. So the equation turns into a simple addition problem.
Positive – Negative = Positive + Positive
For example, let’s say we have the problem $2 − (− 4)$. This reads “two minus negative four.” The $− (− 4)$ turns into $+ 4$.
On the number line we start at 2.
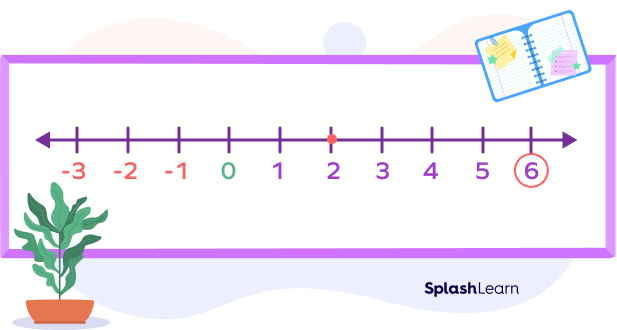
Then we move forward three units: $2 + 4$.
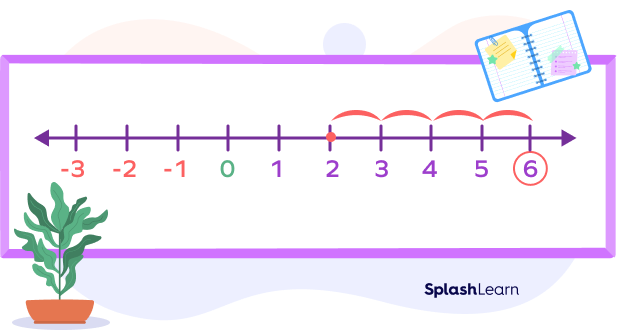
The answer is $2 − (− 4) = 6$.
Methods of Subtraction
There are various methods for subtraction. In this article, we shall be discussing three of them.
Visual representation
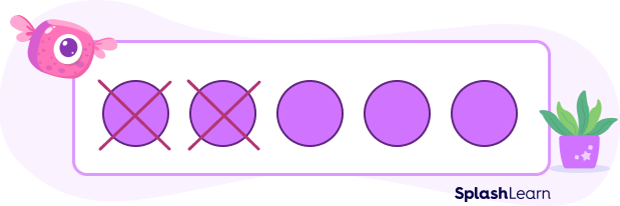
One of the methods is to use a diagram showing what you start with, what you are taking away, and what you are left with.
For example, we have 5 balls, now a friend asks for 2 balls, we can easily calculate that we are left with 2 balls using the concept of subtraction by depicting it through a diagram as given below:
Another method to perform subtraction is by using a number line.
Subtraction on Number Lines
If we want to calculate 5 minus 2, we start from 5. Since we need to subtract 2, we take 2 steps back. Finally we observe that we are standing at 3.
So, this is how $5 − 2$ is calculated on the number line.
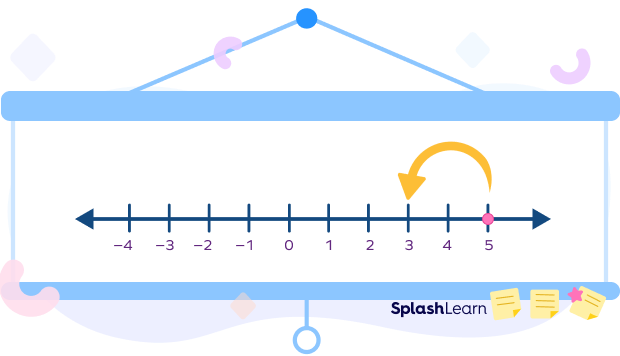
This is a number line representation of the expression.
Column method
The generally used method is the column method of subtraction, where we separate the numbers into ones, tens, hundreds and so on and write the minuend above the subtrahend, where all the ones are in one column, all the tens are in another column and so on. In this method, we always start the subtraction with the ones and proceed from right to left.

Regrouping in Math
Regrouping in math can be defined as the process of making/breaking groups when carrying out operations like addition and subtraction. To regroup means to rearrange groups in place value to carry out an operation. We use regrouping in subtraction, when digits in the minuend are smaller than the digits in the same place of the subtrahend.
This process is called regrouping as we are regrouping numbers or rearranging them into their place value to carry out this process. When we use regrouping in subtraction, it is also sometimes called borrowing.
Subtraction with Regrouping
In subtraction, we sometimes use the concept of regrouping between numbers. When the numbers are subtracted using the column method and the bottom digit is greater than the upper digit, we regroup the numbers to be able to subtract.
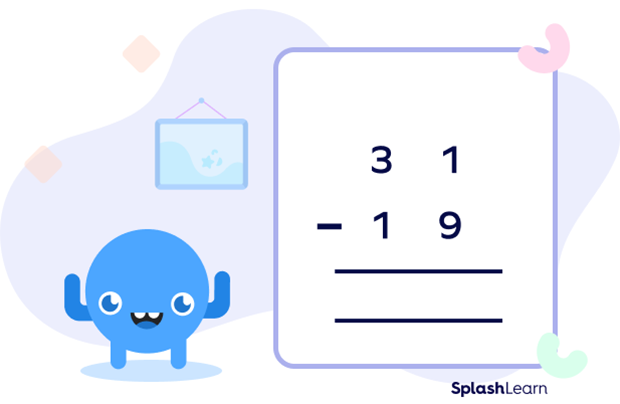
Let us understand subtraction using this regrouping example, which includes finding the answer to the expression $31 − 19$.
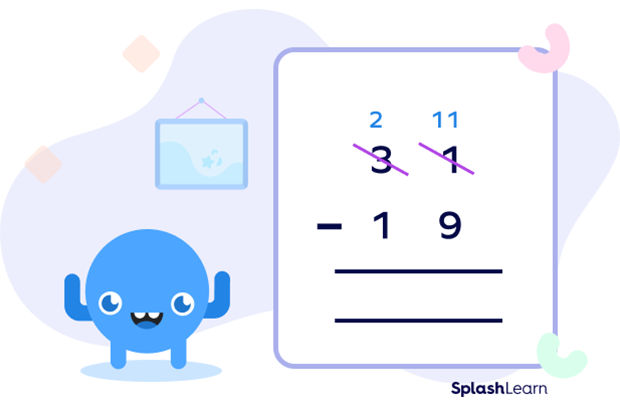
Here, we first subtract the unit place digit of the number in the lower slot with the upper slot. If the number in the lower slot is larger than the number in the upper slot, regrouping takes place, also called borrowing. In this case, we subtract one from the tens place digit from the upper slot number and write the remaining number above it, that is, we take 1 from 3 making it 2 which we wrote above 3, while this 1 that we subtracted is “borrowed” to the unit place, making it a 10 and adding it to the unit place existing number, giving us a two digit number. In simpler words 10 is borrowed from the tens place digit and added to the unit place digit. In the above example, 10 is added to the unit place digit i.e. 1 and we write 11 above the unit place digit.
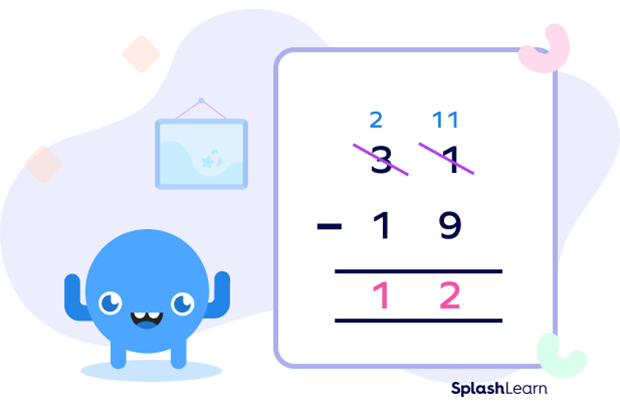
Now, we move on to the real subtraction of the two numbers. The number of the unit place of the upper slot can now be subtracted from the unit place number of the lower slot, i.e. $11 − 9$ giving us 2. While we normally take the remaining number from the upper slot i.e. 2 and subtract the lower slot number from it, i.e., $2 − 1$, giving us 1, which leaves us with 12 as the final answer.
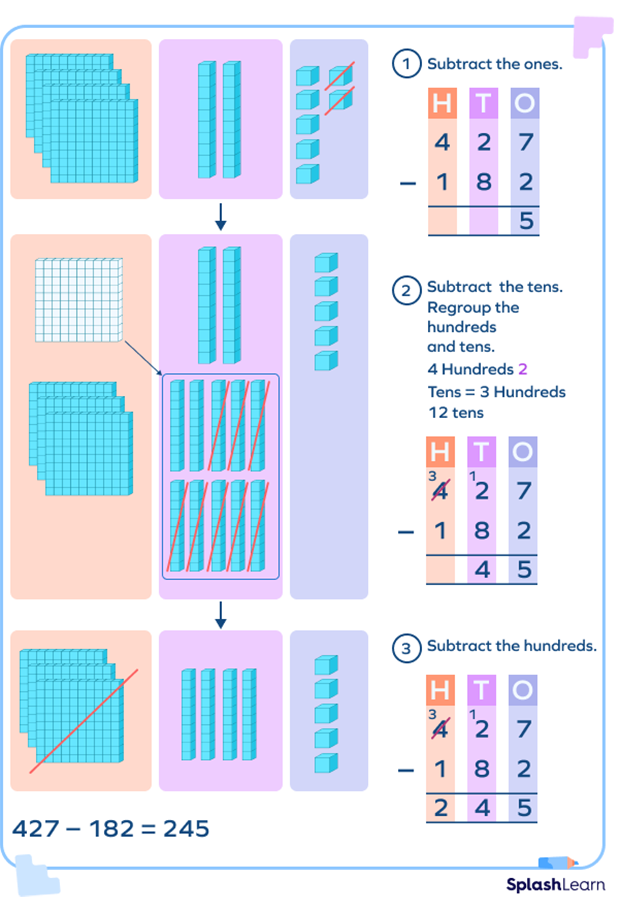
Here’s how we regroup hundred and tens to subtract 182 from 427:
Properties of Subtraction
Here are a few important properties of subtraction in our everyday life.
- Commutative property of subtraction:
Commutative property states that swapping of numbers does not alter the result. But in subtraction, we cannot get the same output when we put minuend in place of subtrahend and vice versa. Hence, commutative property is not possible in case of subtraction.
For example, $8 − 5$ is not equal to $5 − 8$.
- Identity property of subtraction:
Identity property states that when we subtract “0” from a number, the resultant is the number itself.
For example, $5 − 0 = 5$.
- Inverse Property of Subtraction (Subtracting a number by itself):
When we subtract a number from itself, the resultant is always “0.”
$\text{A} − \text{A} = 0$
For example, $9 − 9 = 0$.
According to the property, if we subtract any number on both sides of an equation, the equality of the equation still holds.
For the given algebra equation;
$\Rightarrow \times − 3 = 5$
If we subtract the same number on both sides, the equation will still hold true. Here we will subtract 8 from both sides.
$\Rightarrow \times − 3 − 8 = 5 − 8$
$\Rightarrow \times − 11 = − 3$
- Distributive Property of Subtraction
According to the property, the multiplication of subtraction of numbers is equal to subtraction of the multiplication of individual numbers.
$\text{A} \times (\text{B} − \text{C}) = \text{A} \times \text{B} − \text{A} \times \text{C}$
For example: $3 \times (5 − 2) = 3 \times 3 = 9$ and $3 \times 5 − 3 \times 2 = 15 − 6 = 9$
Conclusion
In this article, we have learned about subtraction, its definition with example, the symbols used for it, the common methods used for subtraction. We also learned about the minus sign. The minus sign is used for different purposes. Let’s practice our understanding with a few solved examples and practice problems and solved examples.
Solved Examples On Subtraction
1. In a soccer match, Team A scored 5 goals and Team B scored 9 goals. Which team scored more goals and by how much?
Solution:
Goals scored by Team $\text{A} = 5$;
Goals scored by Team $\text{B} = 9$
We can clearly see that Team B scored more goals. To calculate the numbers of goals by which Team B exceeded, we will subtract 5 from 9.
$9 − 5 = 4$
Therefore, Team B scored 4 more goals than Team A.
2. Jeff has 120 pens. Her friend Tim has 50 pens less than Jeff. How many pens does Tim have?
Solution:
As we know, the term “less than” refers to the operation subtraction.
Given,
Jeff $= 120$
Tim $= 120 − 50 = 70$
Therefore, Tim has 70 pens.
3. During an annual Easter egg hunt, the participants found 52 eggs in the clubhouse, out of which 14 Easter eggs were broken. Can you find out the exact number of unbroken eggs?
Solution:
The number of easter eggs found in the Clubhouse $= 52$;
Number of easter eggs that were broken $= 14$;
The total number of unbroken eggs $=$ ?
Now, we will subtract the number of broken eggs from the total number of eggs.
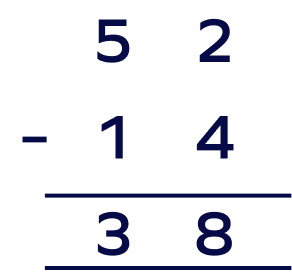
Therefore, the number of unbroken eggs is 38.
4. Jerry collected 194 fishes and Evan collected 132 fishes. Who collected more fish and by how much?
Solution:
Number of fishes collected by Jerry $= 194$;
Number of fishes collected by Evan $= 132$
This shows that Jerry collected more fish. Let us subtract $194 − 132$ to get the difference.
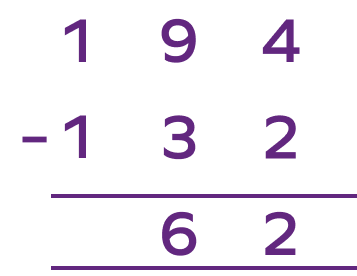
Therefore, Jerry collected 62 fish more than Evan.
5. By how much is 5251 less than 6556?
Solution:
From the given, it is clear that 6556 is greater than 5251 .
Now subtract 5251 from 6556.
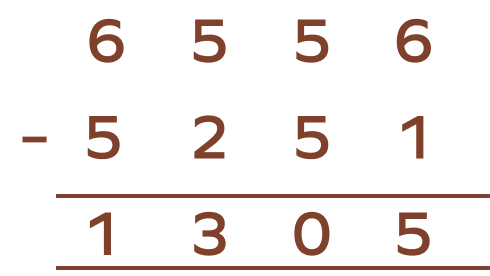
$6556 − 5251 = 1305$
Therefore, 5251 is less than 6556 by 1305.
6. What is the value of 794 minus 658?
Solution: $794 − 658 = 136$
7. When Steve woke up, his temperature was $101^{\circ} \text{F}$. Two hours later, it was 3º lower. What was his temperature after two hours?
Solution: Temperature at the time of Steve waking up $= 101^{\circ} \text{F}$
Temperature after 2 hours $= 101^{\circ} \text{F} − 3^{\circ} \text{F} = 98^{\circ} \text{F}$
8. What will be the coordinates of A if $x = −5$ and $y = − 7$. In which quadrant will A lie?
Solution: Since it is given that $x = − 5$ and $y = − 7$, the coordinates of A will be $(− 5, − 7)$. Also, as both the coordinates are negative, i.e., $( − x, − y)$, A will lie in the third quadrant.
9. An elevator is on the eighteenth floor. It goes down 13 floors. What floor is the elevator on now?
Solution: The floor on which the elevator is now $= 18 − 13 = 5$th floor
10. Is $(4 − 6) = (6 − 4)$?
Solution: Let us find the solution to both of them.
On the left side, $4 − 6 = − 2$
Whereas, on the right side, $6 − 4 = 2$
We can clearly see that $2 \neq − 2$.
So, $(4 − 6)$ is not equal to $(6 − 4)$.
Practice Problems On Subtraction
Subtract - Definition with Examples
On subtracting 69 from 108, we get
Let’s use the steps for subtraction with regrouping.
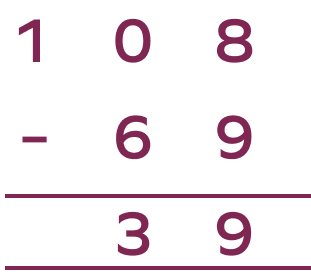
What is the difference between 155 and 56?
Let’s use the steps for subtraction with regrouping.
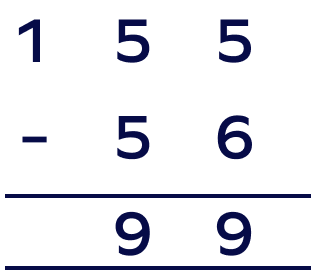
Derek has 25 apples and he gave 18 apples to his brother. How many apples is Derek left with?
Here, we will subtract 18 from 25 to find the answer.
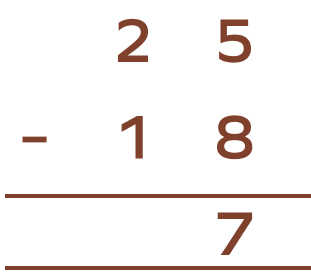
Look at the given number line. What equation would correctly match the solution on the number line?
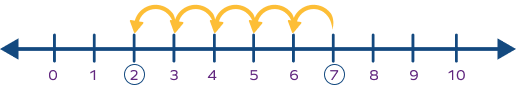
Starting from 7, we took 5 steps back and landed on 2. So, the image shows the equation $7 − 5 = 2$.
On subtracting 1267 from 1513, we get
C
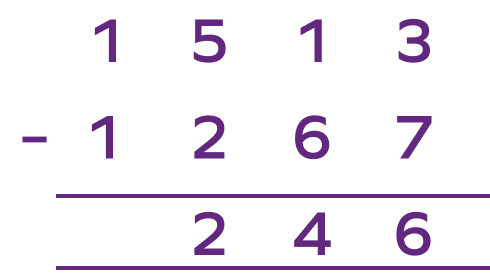
Frequently Asked Questions On Subtraction
Why is the answer to a subtraction problem called the difference?
Because if you subtract a smaller number from a bigger number the result is the difference between the two numbers.
Example: Subtract 2 from 6
$6 − 2 = 4$
But, the number 6 is also 4 bigger than 2. It is the difference between the two numbers.
Which other operation has the output smaller than the input?
Another operation where the output is smaller than the input is division.
Is subtraction associative?
No, subtraction is not associative. Let us look at it using an example. $10 − (5 − 1) \neq (10 − 5) − 1$
Can we subtract a larger number from a smaller number?
Yes, we can subtract a larger number from a smaller number. The resultant will be a negative number.
Mathematically speaking, why does subtraction by “counting up” work?
When we subtract 2 numbers, we can do it in two ways. Let’s take an example of subtracting 5 from 8. You can either take 8 and subtract 5 from it, or you can begin with 5 and count up to 8. When you begin with 5 and count up to 8, you do it 3 times: 6, 7 and 8. So, 3 will be the difference between 5 and 8.
What is the difference between minus sign and plus sign?
Minus sign is denoted by a horizontal symbol, i.e., $−$, and it means to subtract or take away. Whereas, the plus sign is denoted by intersection of horizontal and vertical lines, i.e., $+$ which means to add or find the sum.
Does commutative property hold true for subtraction?
The commutative property does not hold for subtraction. It means for any two whole numbers, $\text{A} − \text{B} \neq \text{B} − \text{A}$.For example: $3 − 5 = − 2$ and $5 − 3 = 2$ and $− 2 \neq 2$.
Does Associative property hold true for subtraction?
The associative property does not hold for subtraction. It means for any three whole numbers A, B, and C.
$\text{A} – (\text{B} – \text{C}) \neq (\text{A} – \text{B}) – \text{C}$ For example: $(2 – 3) – 5 = – 1 – 5 = – 6$ and $2 – (3 – 5) = 2 + 2$ and $– 6 \neq 4$.
What is a minuend and a subtrahend?
In a subtraction equation, minuend is the highest number from which a component would be subtracted. A subtrahend is the term that denotes the number being subtracted from another.
Who discovered the minus sign?
Robert Recorde introduced the modern use of minus to the UK in 1557. The first appearance of the minus sign was given by Johannes Widmann in 1489 and was found in his book called “Mercantile Arithmetic.”




































