- What is the Subtraction Property of Equality?
- Subtraction Property of Equality Formula
- Subtraction Property of Equality Including Fractions
- Solved Examples on Subtraction Property of Equality
- Practice Problems on Subtraction Property of Equality
- Frequently Asked Questions on Subtraction Property of Equality
What is the Subtraction Property of Equality?
The subtraction property of equality states that subtracting the same number from both sides of an equation maintains the equality. An algebraic equation is a mathematical statement that uses the “equal to sign” or “$=$” to state that two expressions are equal.
Examples: $5 + 7 = 12$
$13 \;–\; 4 = 9$
$y + 6 = 10$
When we have a mathematical equation, the balanced operations of addition, subtraction, multiplication, and division on both sides do not affect the equality.
If any mathematical operation is applied on one side of an equation, then it must be applied on the other side of an equation to keep it balanced. The properties that do not impact equality are called the properties of equality.
Subtraction Property of Equality Definition
The subtraction property of equality states that subtracting the same number from both sides of an equation does not affect the equality. If the same number or value is subtracted from two sides of an equation, then the equality also holds for the difference obtained on both sides.
Mathematically, we can express this as
If $a = b$, then $a \;–\; c = b \;–\; c$.
The converse is also true!
Thus, we get
$a = b\Rightarrow a \;–\; c = b \;–\; c$
Example 1: Alice has 2 chocolates and Janice has 5 chocolates. How many chocolates do both have?
Number of chocolates both have $= 2 + 5 = 7$
Now suppose Alice and Janice eat one chocolate each, then how many chocolates will both have?
L.H.S. $= 2 + 5 \;-\; 1 = 6$
R.H.S. $= 7 \;-\; 1 = 6$
L.H.S. $=$ R.H.S.
We can see that subtracting 1 from both sides maintains equality.
Example 2: Solve $x + 5 = 9$.

Recommended Games
Subtraction Property of Equality Formula
Consider an equation $x = y$.
If a real number “c” is subtracted from L.H.S. and R.H.S., then we get $x \;–\; c = y \;–\; c$.
So, the formula is given by,
$x = y \Longleftrightarrow x \;–\; c = y \;–\; c$
So, equality holds or the equation is balanced if the same number is subtracted from both sides of the equation.
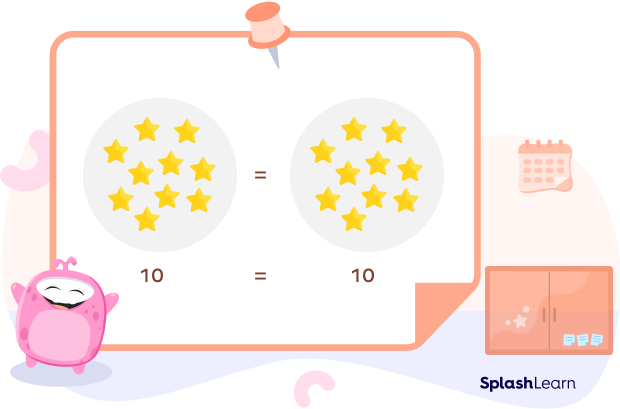
Consider an example of the subtraction property of equality: Consider two circles with the same number of stars.
Stars in Circle $1 =$ Stars in Circle 2
$\Rightarrow 10 = 10$
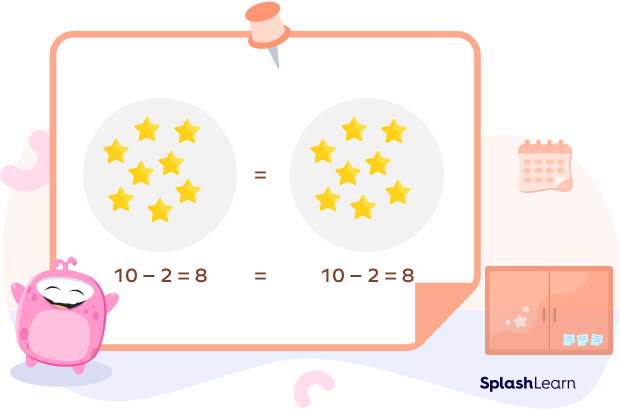
Now, if we take away 2 stars from Circle 1 then, in order to balance this equation in both the circles, we need to take away 2 stars from the other circle also.
Recommended Worksheets
Verification of Subtraction Property of Equality
Let’s verify the property with examples.
Example 1: Arithmetically, we know that $15 + 8 = 23$.
Now, if we subtract 5 from both sides of the equation, we have
L.H.S. $= 15 + 8 \;–\; 5 = 18$
R.H.S. $= 23 \;–\; 5 = 18$
L.H.S. $=$ R.H.S.
It implies that when the same number is subtracted from both sides of an equation, the equality still holds or the equation is balanced.
Example 2: Now, let us take another example. Let us consider an algebraic equation $x + 5 = 37$. To find the value of x, we need to subtract 4 from both sides of the equation. So, we have
$x + 5 = 37$
$\Rightarrow x + 5 \;–\; 5 = 37 \;–\; 5$
$\Rightarrow x = 32$
So, the property is extremely useful in solving the algebraic equations.
Subtraction Property of Equality Including Fractions
Consider an equation involving fractions $\frac{a}{b} = \frac{p}{q}$ . Subtracting the same fraction $\frac{c}{d}$ from both sides of the equation keeps the equation balanced.
$\frac{a}{b} = \frac{p}{q} \Rightarrow \frac{a}{b}\;-\;cd = pq \;-\; cd$
Conclusion
In this article, we learned about the subtraction property of equality. It states that if we subtract the same number on both sides of an equation, then the equation remains balanced. Let’s solve a few examples!
Solved Examples on Subtraction Property of Equality
1. John has 10 balloons in one hand and 10 in another. A bird bursts 3 balloons on the left side. How should he balance the number of balloons in each hand?
Solution:
Initially, John is holding 10 balloons in both of his hands.
$10 = 10$
Then, 3 balloons on the left side were burst by a bird, resulting in a loss of balance.
Number of balloons in the left hand $= 10 \;–\; 3 = 7$
To balance the other side, John lets go of 3 balloons from the right side.
$7 = 10 \;–\; 3$
$\Rightarrow 7 = 7$ [Equation is balanced.]
2. Let x be a real number such that $x + 6 = 18$. Find the value of $x$.
Solution: $x + 6 = 18$
$x + 6 = 18$
To solve for $x$, it is necessary to isolate the variable. In this case, subtracting 6 from the left side of the equation will do that.
Subtract 6 from both sides of the equation to get:
$x + 6 \;-\; 6 = 18 \;-\; 6$
$x = 12$
3. Let a,b and c be real numbers such that $b = c$ and $c = 4 + a$. Show that $b \;-\; a = 4$.
Solution:
$b = c$
$c = 4 + a$
Subtracting a from both the sides, we get
$c\;-\;a = 4 + a\;-\;a$
$c\;-\;a = 4$
Since, $b = c$
$b \;-\; a = 4$
4. Let $x + 7 = 18$ and $y + 5 = 21$. Find the value of $x$ and $y$.
Solution:
$x + 7 = 18$
Subtracting 7 from both the sides, we get
$x + 7 \;-\; 7 = 18 \;-\; 7$
$x = 11$
$y + 5 = 21$
Subtracting 5 from both the sides, we get
$y + 5 \;-\; 5 = 21 \;-\; 5$
$y = 16$
Practice Problems on Subtraction Property of Equality
Subtraction Property of Equality – Definition with Examples
Find the value of $x$ for the algebraic equation $x + 12 = 17$.
On subtracting both the sides by 12, we get: $x + 12-12 = 17\;-\;12 x=5$
If $x = y$, then choose the correct option:
If $x = y$, $x\;-\;5 = y\;-\;5$ by the subtraction property.
Find the value of $x,\; \frac{2}{3} + x = \frac{3}{4}$.
On subtracting $\frac{2}{3}$ from the sides, we get $\frac{2}{3} + x\;-\;\frac{2}{3} = \frac{3}{4}\;-\;\frac{2}{3}$
$x = \frac{9\;-\;8}{12} = \frac{1}{12}$
The subtraction property of equality formula is given by:
The subtraction property equality states that we have to subtract same number from both the sides, i.e., if $x = y$, so $x\;-\;c = y\;-\;c$.
Two bags of wheat have the same weight. If 12 ounces of wheat are removed from each bag, how do the new weights of the bags compare to each other?
Let $a$ and $b$ be the weight of the wheat in the first and second bag respectively. Since both bags have same weight, so $a = b$. On removing 12 ounces from each bags, we get $a\;-\;12 = b\;-\;12$
Frequently Asked Questions on Subtraction Property of Equality
What is the difference between the subtraction property of equality and the addition property of equality?
The subtraction property of equality is the property that states that if a value is subtracted from two equal quantities, then the differences are also equal, i.e., if $X = Y$, then $x /;-/; c = y /;-/; c$.The subtraction property of equality is that property which states that if a value is added from two equal quantities, then the sums are also equal, i.e., if $X = Y$, then $x + c = y + c$.
What is the subtraction property of inequality?
According to the subtraction property of inequality, if the same number is subtracted from both sides of any given inequality, then the sense or the sign of the inequality remains the same.
Can the number which we subtract from both the sides of an equation be 0?
Yes, the number which we subtract from both sides of an equation can be 0. However, subtracting 0 does not change the equation.
How can we deduce the addition property of equality using the subtraction property of equality?
We can deduce the addition property of equality by subtracting $(/;-/;c)$ from both the sides of $x = y$.
$x/;-/;(/;-/;c) = y/;-/;(/;-/;c)x + c = y + c$ which is the addition property of equality.
What are the applications of the subtraction property of equality?
We are able to manipulate, simplify, balance, and solve equations, as well as draw accurate conclusions supported by reasons using the subtraction property of equality. It also helps in simplifying the complex algebraic expressions.
What are the nine properties of equality?
There are nine properties of equality:
1. Addition
2. Subtraction
3. Multiplication
4. Division
5. Reflexive
6. Symmetric
7. Transitive
8. Substitution and
9. Square root
What are the properties of subtraction?
- Identity property: $a /;-/; 0 = a$
- Change of order: $a /;-/; b = /;-/;(b /;-/;a)$
- Subtracting a number from itself: $a /;-/; a = 0$




































