What Are Whole Numbers?
In our daily life, we use counting numbers, which are 1, 2, 3, ….. and so on. Whole numbers is a collection of all the basic counting numbers and 0. In mathematics, counting numbers are called natural numbers. So, we can define the whole number as a collection of all natural numbers and 0. Whole numbers also include all positive integers along with zero.
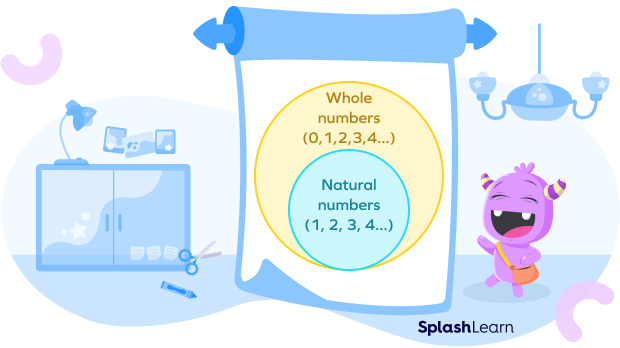
Whole numbers include natural numbers that begin from 1 onwards.
Let us look at some examples of whole numbers.
| Whole Numbers | NOT Whole Numbers |
| 0, 14, 97, 345, 8901, and 888888 | -5 (Negative numbers), 7.3 (Decimals), ⅘ (Fractions) |
The set of whole numbers is denoted by the alphabet ‘W‘.
W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,.…}
Recommended Games
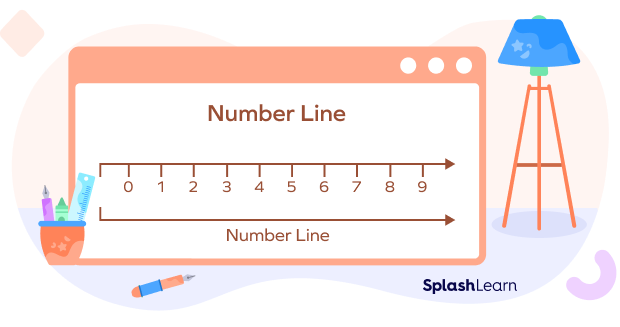
Whole Numbers on Number Line
The set of whole numbers can be displayed on the number line as shown below.
Smallest and Largest Whole Number
The smallest whole number is 0. In whole numbers, 0 has no predecessor or a number that comes before. There is no ‘largest’ whole number.
Recommended Worksheets
Properties of Whole Numbers
The basic operation of addition, subtraction, multiplication, and division give rise to four main properties of whole numbers.
- Closure Property:
The sum and product of two whole numbers is always a whole number and is closed under addition and multiplication.
Consider two whole numbers, 5 and 8.
5 + 8 = 13; a whole number
5 × 8 = 40; a whole number
- Commutative Property:
The sum and product of whole numbers are the same even if the order of the numbers are interchanged.
Consider two whole numbers, 2 and 7.
2 + 7 = 7 + 2 = 9
2 × 7 = 7 × 2 = 14
The commutativity property holds true for addition and multiplication.
- Associative Property:
How the whole numbers are grouped during addition or multiplication does not change the sum or product.
Consider three whole numbers, 2, 3, and 4.
2 + (3 + 4) = 2 + 7 = 9
(2 + 3) + 4 = 5 + 4 = 9
Thus, 2 + (3 + 4) = (2 + 3) + 4
2 × (3 × 4) = 2 × 12 = 24
(2 × 3) × 4 = 6 × 4 = 24
Thus, 2 × (3 × 4) = (2 × 3) × 4
- Distributive Property:
The multiplication of a whole number is distributed over the total or difference of the whole numbers. Applying the distributive property makes the equation easier to solve.
Consider three whole numbers, 9, 11, and 6.
9 × (11 + 6) = 9 × 17 = 153
(9 × 11) + (9 × 6) = 99 + 54 = 153
Thus, 9 × (11 + 6) = (9 × 11) + (9 × 6)
Difference between Whole Numbers and Natural numbers
| Whole Numbers | Natural Numbers |
| Whole numbers include all natural numbers and zero. | Natural numbers are generally used for counting objects or things. |
| The set of whole numbers is, W = {0,1,2,3,…}. | The set of natural numbers is, N = {1,2,3,…}. |
| The smallest whole number is 0. | The smallest natural number is 1. |
From these differences, we can easily deduce that every whole number other than 0 is a natural number. We can say that the set of natural numbers is a subset of whole numbers.
Fun Facts
- There is no ‘largest’ whole number.
- Every whole number has an immediate predecessor, except 0.
- A decimal number or a fraction that falls between two whole numbers is not a whole number.
Conclusion
In a nutshell, we can say that whole numbers are a pivotal part of the number system that includes all the positive integers from 0 to infinity. To learn more concepts like natural numbers and real numbers, check out the game-based learning platform, SplashLearn. With fun activities and courses, it aims to transform K-8 learning and equip children with the skills required in the 21st-century.
Solved Examples on Whole Numbers
Q1. Add the numbers in three different ways. Indicate the property used.
25 + 36 + 15
Solution:
(a) 25 + 36 + 15
Method I: 25 + (36 + 15) = 25 + 51 = 76
Method II: (25 + 36) + 15 = 61 + 15 = 76
Method III: (25 + 15) + 36 = 40 + 36 = 76
Here, we have used associative property.
Q2. Solve 6 × (8 – 3) using the distributive property of multiplication.
Solution:
Applying the distributive law formula a(b + c) = ab + ac
6 × (8 – 3)
= 6(8) – 6(3)
= 40 – 18
= 22
Q3. Under what condition is the product of two whole numbers zero?
Solution:
If the product of 2 whole numbers is zero, then one of them is surely zero.
For example, 0 × 5 = 0 and 19 × 0 = 0
If the product of 2 whole numbers is zero, then both of them may be zero.
0 × 0 = 0
The product of two whole numbers is zero under the condition that one or both of them are zero.
Practice Problems on Whole Numbers
Whole Numbers
What are the next three whole numbers after 1099?
Every whole number other than 0 is a natural number, so the next three numbers following 1099 are natural numbers.
How many whole numbers are there in between 22 and 35?
Whole numbers between 22 and 35: 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34
Which of the following is equal to 636 x 102.
636 × (100 + 2) = 636 × 102
Find the product of 6 × (40 + 2).
Using the distributive formula, $6 × (40 + 2) = (6 × 40) + (6 × 2) = 240 + 12 = 252$
Frequently Asked Questions on Whole Numbers
Give some examples and non-examples of whole numbers.
A whole number is any positive number that does not include a fractional or decimal part, and zero.
Examples: 0, 1, 2, 3, 4, 5, 6, and 7
Non-examples: 3, 2.7, or 3 ½
Can we write 1/2 as a whole number?
No, we cannot write the given fraction as a whole number. Whole numbers do not include fractional or decimal numbers.
We can round up ½ or 0.5 to 1 or down to 0.
What are whole numbers used for?
Whole numbers are used as building blocks to impart an in-depth understanding of more complex number identifiers like real numbers, rational numbers, and irrational numbers. By rounding a decimal number to the nearest whole number, we can simplify calculations and solve problems faster.




































