Hamburger menu

What Are Natural Numbers? Definition, Properties, Types, and Examples

Home » Math Vocabulary » What Are Natural Numbers? Definition, Properties, Types, and Examples

What Are Natural Numbers?

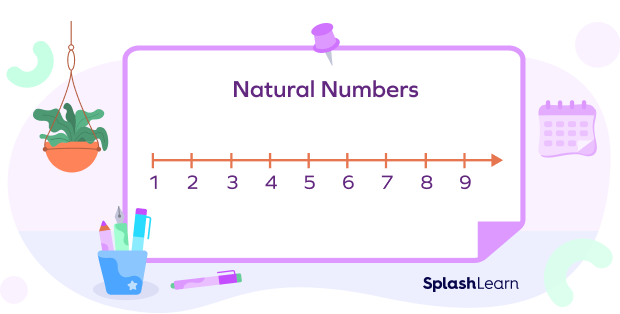
Natural numbers are 1, 2, 3, 4, 5, 6, and go on till infinity. They are also called counting numbers, as they are used to count objects. Natural numbers do not include 0 or negative numbers. The symbol ℕ is used to represent the set of natural numbers. 

Natural numbers on a number line

Definition of Natural Numbers

Natural numbers are all positive integers from 1 to infinity. They are also called counting numbers as they are used to count objects. Natural numbers do not include 0 or negative numbers. 

We need numbers in our everyday lives, be it for counting objects, telling time, numbering houses, etc. Numbers that help us count and represent quantities are called natural numbers. These include 1, 2, 3, 4, 5, 6, and go on until infinity. 

Here we can see that 1 is the smallest natural number and each subsequent natural number is exactly one more than the previous one. Thus, the numbers that come in between these numbers are not natural numbers like fractions, decimals etc. 

Types of Natural Numbers

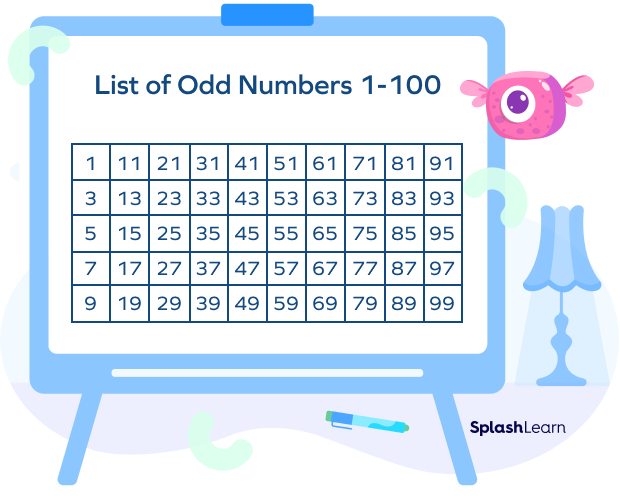
  1. Odd Natural Numbers

The odd natural numbers are the positive numbers not divisible by 2.

For example: 29, 677, 89901 etc.

List of odd numbers within 100
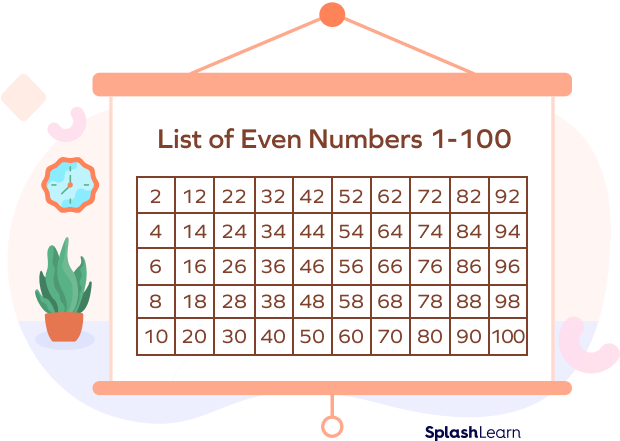
  1. Even Natural Numbers

The even natural numbers are the positive numbers that are divisible by 2. 

For example: 28, 456, 6022 etc. 

List of even natural numbers within 100

What Are the Properties of Natural Numbers?

Properties of natural numbers in mathematics are certain rules that can be applied or the characteristics of natural numbers that can be used when we perform arithmetic operations on them.

The four basic properties of natural numbers are:

  • Closure Property 
  • Associative Property
  • Commutative Property 
  • Distributive Property

The basic operations of addition, subtraction, multiplication, and division give rise to four main properties of natural numbers. 

Properties of natural numbers: closure, associative, commutative, distributive

The image shown above gives a quick overview of each property. Let’s understand each property in detail with examples.

Properties of Natural Numbers

Here are the significant properties of natural numbers:

  • Closed under addition and multiplication
  • Follows the associative property of addition and multiplication
  • Follows the distributive property of multiplication over addition and subtraction

Closure Property of Addition and Multiplication

  • Closure property of addition: When you add two natural numbers, the result will always be a natural number. 

Examples of closure property of addition: 2 + 2 = 4, 3 + 4 = 7, 5 + 5 = 10 

In each case, the result of the addition of natural numbers is a natural number. 

  • Closure property of multiplication: When you multiply two natural numbers, the result will always be a natural number. 

Examples of closure property of multiplication: 2 × 2 = 4, 3 × 2 = 6, 5 × 5 = 25 

In each case, the result of the multiplication of natural numbers is a natural number. 

Thus, we say that the natural numbers are closed under addition and multiplication.

The question remains: Are natural numbers closed under division and subtraction? In case of division and subtraction, the closure property does not hold true. Subtracting or dividing two natural numbers will not always give us a natural number.

  • Examples of subtraction: 4 – 6 = –2, 5 – 3 = 2, 6 – 9 = –3 

The second case resulted in a natural number, but the first and third examples did not.  

  • Examples of division: 10 ÷ 3 = 3.33, 9 ÷ 3 = 3, 15 ÷ 4 = 3.75 

The first and third cases did not result in natural numbers.  

Associative Property of Addition and Multiplication

  • Associative property of addition: The sum of natural numbers remains unchanged even if the grouping of numbers is changed. It is expressed as an equation as a + (b + c) = (a + b) + c.

Examples of associative property of addition: 2 + (5 + 6) = 13 and (2 + 5) + 6 = 13 

  • Associative property of multiplication: The product of natural numbers remains unchanged even if the grouping of numbers is changed. It is expressed as an equation as a × (b × c) = (a × b) × c.

Examples of associative property of multiplication: 2 × (3 × 4) = 24 and (2 × 3) × 4 = 24 

The associative property does not hold for subtraction and division.

a − (b − c) ≠ (a − b) − c 

a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c

Examples of subtraction: 4 -(10 − 2) = − 4 and (4 − 10) − 2 = − 8 

Examples of division: 5 ÷ (6 ÷ 3) = 2.5 and (5 ÷ 6) ÷ 3 = 0.27

Commutative Property of Addition and Multiplication

  • Commutative Property of Addition: If we change the order of natural numbers in addition, the result does not change. 

Examples of commutative property of addition: 6 + 5 = 11 and 5 + 6 = 11

  • Commutative Property of Multiplication: If we change the order of natural numbers in multiplication, the result does not change. 

Examples of commutative property of multiplication: 2 × 4 = 8 and 4 × 2 = 8 

The commutative property does not apply to subtraction and division of natural numbers. 

Examples for subtraction and division:

a − b ≠ b − a  

a ÷ b ≠ b ÷ a

Examples for subtraction: 5 − 3 = 2 and 3 − 5 = − 2

Examples for division: 6 ÷ 3 = 2 and 3 ÷ 6 = 0.5 

Distributive Property

  • Distributive property of multiplication over addition: According to the distributive property of multiplication over addition, if we multiply the total of two addends by a number or multiply each addend individually and then add them, the result will be the same. 

Distributive property of multiplication over addition: a(b + c) = (a × b) + (a × c)

Example: 2 × (5 + 3) = 16

       (2 × 5) + (2 × 3) = 16

This property also holds in the case of multiplication over subtraction. 

  • Distributive property of multiplication over subtraction: a(b − c) = (a × b) − (a × c)

Example: 2 × (5 – 3) = 4

               (2 × 5) – (2 × 3) = 4

History of Natural Numbers 

It is widely accepted that natural numbers (starting from one) arose from the practical need to count objects. This development is tied to early human societies across the world as they began to manage resources, trade, and keep records.

Fun Facts about Natural Numbers

  • There are an infinite number of natural numbers. There is no largest natural number. Natural numbers go on forever. The smallest natural number is 1. 
  • You will get the next natural number by simply adding 1 to a given natural number.
  •  For the natural number 1, there is no “predecessor” or a previous natural number.
  •  (1 = 0 + 1, but we know that 0 is not a natural number).
  • Natural numbers are also called counting numbers, as they are used to count objects.
  • The properties of natural numbers do not hold true in the case of division and 
  • subtraction.
  • Negative numbers, fractions, and decimals are neither natural numbers nor whole numbers.
  • Even natural numbers = E = {2, 4, 6, 8, 10, …}
  • Odd natural numbers = O = {1, 3, 5, 7, 9, 11, …}

Conclusion

In this article, we learned about natural numbers and its properties. These properties make the natural number set unique. In this process, we also understand that the division and subtraction of natural numbers is not guaranteed to be a natural number but that there are incidences where the result is a natural number. Now, let’s apply this knowledge to solve some examples.

Solved Examples on Natural Numbers

  1. Identify natural numbers from the following list. 

             10, $\frac{1}{6}$, 4.66, 22, 1564, –6. 

Solution:

The natural numbers are 10, 22, and 1564. Negative numbers, decimal numbers, and fractions are not considered natural numbers.

  1. List the first ten natural numbers. 

Solution:

 The answer is 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10, as the natural numbers start from 1. 

  1. What is the difference between any two consecutive natural numbers? 

Solution:

The difference between any two consecutive natural numbers is always 1.

4. Which of the following numbers are natural numbers? 

2, 18, –5, 25.5, 1, –20. 

Solution: 

Natural numbers are given by 1, 2, 3, 4, 5, … and so on.

The numbers 2, 18, and 1 are natural numbers.

The numbers -5 and -20  are not natural numbers because they are negative.

25.5 is not a natural number because it is a decimal.

5. State whether each of the given statements is True or False.

  1. There is always a natural number between two consecutive natural numbers.
  2. Subtraction of two natural numbers is always a natural number.
  3. Natural numbers do not include 0.

Solution: 

  1. The statement is false. Between two consecutive natural numbers, there is no natural number. 

For example, no natural number exists between 1 and 2, as 1.1, 1.2, 1.3, 1.7, 1.9, etc. are decimal numbers.

  1. The statement is false. The natural numbers are not closed under subtraction. It means subtracting two natural numbers may or may not give a natural number.
  2. True. 0 is not a natural number. It is a whole number.

6. Solve the expression 2 (20 + 15) using the distributive property of multiplication over addition.

Solution: 

According to distributive property, we have 

a(b + c) = (a × b) + (a × c)

2 (20 + 15) = (2 × 20) + (2 × 15) = 40 + 30 = 70 

Thus, 2 (20 + 15) = 70

7. Identify the properties of the natural numbers based on the expressions given below:

a) 2 + (5 + 6) = (2 + 5) + 6

b) (10 + 15) = (15 + 10)

c) 4 × (6 × 8) = (4 × 6) × 8 

Solution: 

a) 2 + (5 + 6) = (2 + 5) + 6 

This is an example of the associative property of addition. 

b) (10 + 15) = (15 + 10) 

This is an example of the commutative property of addition.

c) 4 × (6 × 8) = (4 × 6) × 8 

This is an example of the associative property of multiplication.

Practice Problems on Natural Numbers

Natural Numbers

Attend this Quiz & Test your knowledge.

1

Identify a natural number.

– 1
1.0
$\frac{1}{2}$
0.1
CorrectIncorrect
Correct answer is: 1.0
1.0 = 1
1 is a natural number.
(Don’t get confused! 1.0 is just a decimal notation of the natural number 1.)
2

If m and n are two natural numbers, then:

m + n = n + m
m – n = n – m
m ÷ n = n ÷ m
None of these
CorrectIncorrect
Correct answer is: m + n = n + m
As the commutative property states, if we change the order of natural numbers during multiplication and addition, the result will not change. This property does not apply to subtraction and division.
3

Which property of natural numbers holds for 2 + (5 + 6) = 13 and (2 + 5) + 6 = 13?

associative property of multiplication
associative property of subtraction
associative property of addition
closure property of addition
CorrectIncorrect
Correct answer is: associative property of addition
The associative property of addition holds for the given problem. The property states that the sum of natural numbers remains unchanged even if their grouping is varied.
4

Which of the following examples correctly represents commutative property?

6 + 5 = 11 and 5 + 6 = 11
2 + (5 + 6) = 13 and (2 + 5) + 6 = 13
2 × (5 + 3) = (2 x 5) + (2 x 3) = 16
4 – 6 = –2
CorrectIncorrect
Correct answer is: 6 + 5 = 11 and 5 + 6 = 11
The commutative property states that changing the order of natural numbers during multiplication and addition will not change the result.
5

The smallest natural number is _______.

0
1
2
– 1
CorrectIncorrect
Correct answer is: 1
The smallest natural number is 1.
6

Natural numbers do not follow the closure property under _______.

addition
multiplication
subtraction
None of the above
CorrectIncorrect
Correct answer is: subtraction
The subtraction of two natural numbers may not be a natural number. The natural numbers are not closed under subtraction.
7

The sum and product of two natural numbers are always natural numbers. This property is called the ______.

associative property
closure property
commutative property
None of the above
CorrectIncorrect
Correct answer is: closure property
According to the closure property, the result will always be a natural number when you add or multiply two natural numbers.
8

If a, b, and c are natural numbers, then (a + b) + c = a + (b + c). This property is called ______.

associative property
closure property
commutative property
None of the above
CorrectIncorrect
Correct answer is: associative property
According to associative property, the sum or product of natural numbers remains unchanged even if the grouping of numbers is changed. It is given in the form of equation as (a + b) + c = a + (b + c)
9

Which of the following is an example of the commutative property of multiplication?

2 × 4 = 4 × $\frac{1}{2}$
2 × 2 = 4
2 × 4 = 4 × 2
2 × (3 × 4) = (2 × 3) × 4
CorrectIncorrect
Correct answer is: 2 × 4 = 4 × 2
According to the commutative property, if we change the order of natural numbers during multiplication, the result does not change.
Thus, 2 × 4 = 4 × 2 = 8

Frequently Asked Questions about Natural Numbers

No, 0 is not a natural number. It is neither positive nor negative. Natural numbers are a subset of real numbers that only include positive integers 1, 2, 3, 4, 5, 6, and so on, while excluding negative numbers, zero, decimals, and fractions. They do not comprise negative numbers or 0.

All natural numbers are whole numbers. Whole numbers include natural numbers and 0.

Natural numbers are used to count objects in the most natural and instinctive manner. If you can count them on your fingers, the numbers can be deemed natural.

The set of natural numbers in mathematics is {1, 2, 3, …}. Since –1 is a negative number, it is not a natural number.

Cardinal numbers are natural numbers or positive integers used for counting. The smallest cardinal number is 1. Examples of cardinal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, and so on.

The associative property applies to the addition and multiplication of natural numbers.
But for subtraction and division of natural numbers, the associative property does not hold.
For example,  $5 – (3 – 2 ) = 4$  and  $(5 – 3) – 2 = 0$
$30 \div (10 \div 5 ) = 15$ and $(30 \div 10) 5 = \frac{3}{5}$

A square of a natural number is a natural number multiplied by itself. Since natural numbers follow the closure property, the square of a natural number is also a natural number. For example, $5^{2} = 5 \times 5 = 25$, and  25 is a natural number.

The square root of a natural number may or may not be a natural number.
For example, the square root of 9 is 3, square root of 16 is 4, which are natural numbers, but the square root of 6 is approximately 2.449, which is not a natural number.

RELATED POSTS