Irrational Numbers

Irrational Numbers – Introduction

We use numbers in daily life for a variety of reasons. Also, we use different types of numbers for different purposes, such as natural numbers for counting, fractions for describing portions or parts of a whole, decimals for precision, etc. Today we will explore ‘Irrational Numbers’ in math, their applications, examples, operations. Let’s begin!

What Are Irrational Numbers?

Irrational numbers are the type of real numbers that cannot be expressed in the rational form $\frac{p}{q}$, where $p, q$ are integers and $q \neq 0$. 

In simple words, all the real numbers that are not rational numbers are irrational.

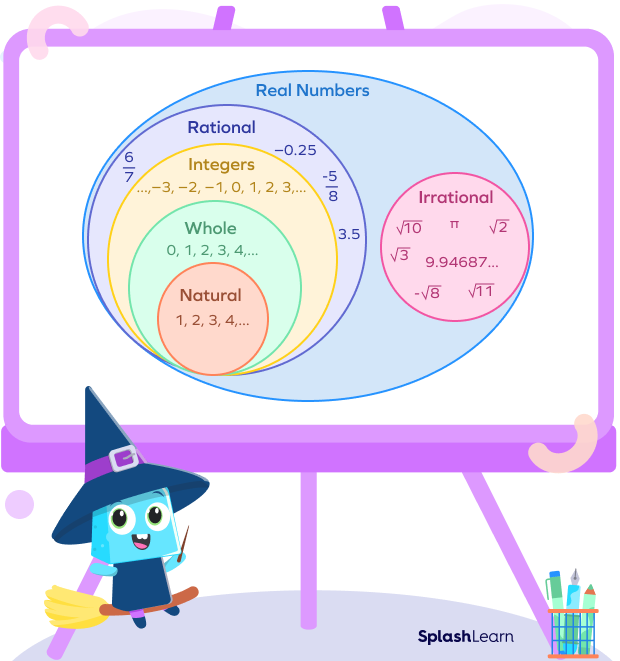
We see numbers everywhere around us and use them on a daily basis. Let’s quickly revise.

• Natural Numbers $= N = {1, 2, 3, 4, . . .}$ 
• Whole Numbers $= W = {0, 1, 2, 3, 4, . . .}$ 
• Integers $= Z = {. . . – 3,-2, -1, 0, 1, 2, 3, . . .}$
• Rational Numbers $= Q$

They include all the numbers of the form $\frac{p}{q}$, where $p, q$ are integers and $q \neq 0$. 

Decimal expansions for rational numbers can be either terminating or repeating decimals.

Examples: $\frac{1}{2} , \frac{11}{3}, \frac{5}{1}$, 3.25, 0.252525 . . .

• Irrational Numbers $= P$

Irrational numbers are the type of real numbers that cannot be expressed in the form $\frac{p}{q}, q \neq 0$. These numbers include non-terminating, non-repeating decimals

• Real Numbers $= R$

           Rational and irrational numbers together make real numbers. 

Irrational Numbers Definition

Irrational numbers can be defined as real numbers that cannot be expressed in the form of $\frac{p}{q}$, where p and q are integers and the denominator $q \neq 0$. 

Example: 

The decimal expansion of an irrational number is non-terminating and non-recurring/non-repeating. So, all non-terminating and non-recurring decimal numbers are “irrational numbers.”

Example: Suppose a square has an area of 5 square meters. Calculate the length of each side.

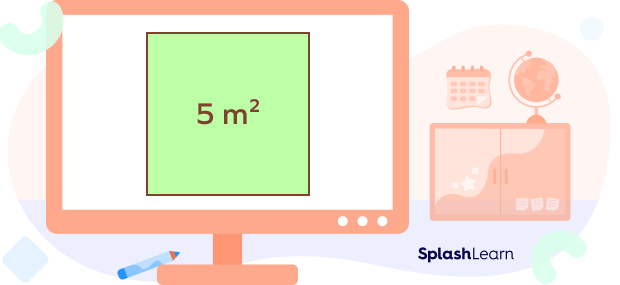
The area of the square = 5 sq. meters

The length of each side is $\sqrt{5}$  meter $=$ 2.23606797749 . . . meter

This answer is in irrational form since we cannot express $\sqrt{5}$ in rational form. Also, the decimal expansion is non-terminating, non-repeating.

Irrational Numbers Examples

The following are examples of a few specific irrational numbers that are commonly used. 

1. In math, we know “pi” as the circumference to diameter ratio. Is pi an irrational number? 

Yes! Pi or is an irrational number. The decimal expansion of $π =$ 3.14159265 . . . is neither terminating nor repeating decimal.

 (Understand that we use pi as 3.14 or $\frac{22}{7}$ to make calculations easier.)

2. $\sqrt{2}$ is an irrational number.
3. Euler’s number e is an irrational number, where $e$ $=$ 2.718281 . . .
4. Golden ratio, $\varphi =$ 1.61803398874989 . . .
5. Square root of non-perfect squares like $\sqrt{26}, \sqrt{63}$, etc.
6. Square root of a prime numbers like $\sqrt{2}, \sqrt{3}$, etc.
7. All non-terminating and non-recurring decimals.

Irrational Numbers List

Here’s a list of some common and frequently used irrational numbers.

• Pi or $\Pi=$ 3.14159265358979…
• Euler’s Number e $=$ 2.71828182845904…
• Golden ratio $\Theta =$ 1.61803398874989….
• $\sqrt{2}$

Irrational Numbers Symbol

Generally, we use the symbol “P” to represent an irrational number, since  the set of real numbers is denoted by R and the set of rational numbers is denoted by Q. We can also represent irrational numbers using the set difference of the real minus rationals, in a way $\text{R} – \text{Q}$ or $\frac{R}{Q}$.

Are all Irrational Numbers Real Numbers?

Rational numbers and irrational numbers together form real numbers. So, all irrational numbers are considered to be real numbers. The real numbers which are not rational numbers are irrational numbers. Irrational numbers cannot be expressed as the ratio of two numbers. However, every real number is not an irrational number.

Properties of Irrational Numbers

The irrational numbers, being a type of real numbers, follow all the properties of real numbers. The following are the properties of irrational numbers: 

• When we add an irrational number and a rational number, it will always give an irrational number.  Example: $\sqrt{3} + \frac{2}{5}$
• When we multiply an irrational number with a non-zero rational number, it will result in an irrational number. Example: $\frac{2}{5} \times \sqrt{3}$
• The LCM (Least Common Multiple) of any two irrational numbers may or may not exist. 
• The addition or the multiplication of two irrational numbers may be rational. 

For example, $\sqrt{3} \times \sqrt{3} = 3$. Here, $\sqrt{3}$ is an irrational number. If we multiply it twice, then the final product obtained is a rational number, 3. 

Also, consider the example of addition of two irrational numbers that gives a rational number. $\sqrt{3} + (2$ $-$ $\sqrt{3} ) = 2$  

It means the set of irrational numbers is not closed under the multiplication process and addition process, unlike the set of rational numbers.

Operations on Two Irrational Numbers

We can do some operations on two or more irrational numbers like addition, subtraction, multiplication, and division. 

Addition

Addition of two irrational numbers may or may not be irrational.

Example 1: $\sqrt{2}$ and $3\sqrt{2}$

$\sqrt{2} + \sqrt{3}2 = \sqrt{2} + 3\sqrt{2} = 3\sqrt{2}$ is an irrational number.

Example 2: $6 + \sqrt{2}$ and $2$ $-$ $\sqrt{2}$

$6 + \sqrt{2} + 2$ $-$ $\sqrt{2} = (6 + 2) + (\sqrt{2}$ $-$ $\sqrt{2}) = 8$ is a rational number.

Subtraction

Subtraction of two irrational numbers may or may not be irrational. 

Example 1: $5 + \sqrt{3}$ and $2$ $-$ $3\sqrt{3}$

$5 + \sqrt{3}$ $-$ $(2$ $-$ $3\sqrt{3}) = (5$ $-$ $2) + (\sqrt{3}$ $-$ $3\sqrt{3}) = 3$ $-$ $2\sqrt{3}$ is an irrational number.

Example 2: $5 + 3\sqrt{3}$ and $4 + 3\sqrt{3}$

$5 + 3\sqrt{3}$ $-$ $( 4 + 3\sqrt{3}) = ( 5$ $-$ $4 ) + ( 3\sqrt{3}$ $-$ $3\sqrt{3}) = 1$ is a rational number.

Multiplication

The product of two irrational numbers may or may not be irrational. 

Example 1: $2\sqrt{3}$ and $6\sqrt{3}$

$2\sqrt{3} \times 6\sqrt{3} =2 \times 3 \times 6 = 36$ is a rational number.

Example 2: $6+\sqrt{2}$ and $2$

$(6 + \sqrt{2}) \times 2 = (6 \times 2) + (\sqrt{2} \times 2) = 12 + \sqrt{2}2$ is an irrational number.

Division

The division of two irrational numbers may or may not be irrational. 

Example 1: $6 \sqrt{2} \div \sqrt{2}$ 

$\frac{6\sqrt{2}}{\sqrt{2}} = 6$ is a rational number.

Example 2: $(5 – \sqrt{2} ) \div \sqrt{2}$

$\frac{5-\sqrt{2}}{2} = \frac{5}{\sqrt{2}}$ $-$ $\frac{\sqrt{2}}{\sqrt{2}} = \frac{5} {\sqrt{2}}$ $- 1$ is an irrational number.

How to Find an Irrational Number between Two Numbers?

Let us find the irrational numbers between 3 and 4.

We know, square root of 9 is 3; $\sqrt{9} = \sqrt{3}$

and the square root of 16 is 4; $\sqrt16 = \sqrt4$

Therefore, $\sqrt{10},\sqrt{11}, \sqrt{12}$, etc., are irrational numbers between 3 and 4. These are not perfect squares and cannot be simplified further. Also, all the non-repeating, non-terminating decimals between 3 and 4 like 3.12537 . . . are irrational.

Rational Numbers vs. Irrational Numbers

The table illustrates the difference between rational numbers and irrational numbers.

Fun Facts

• $\sqrt{2}$ is the first invented irrational number!

Hippasus, the Greek mathematician and the student of the great mathematician Pythagoras proved that “root two” could never be expressed as a fraction.

It was invented while calculating the length of the isosceles right-angled triangle using Pythagoras’ theorem.

$\text{AC}^2 = \text{AB}^2 + \text{BC}^2$

$1^2 + 1^ 2 = \text{AC}^2 \Rightarrow \text{AC} = \sqrt{2}$

$\sqrt{2}$ lies between the rational numbers 1 and 2 as the value of $\sqrt{2}$ is 1.41421 . . .

• Pi day!

14 March or 3/14 is celebrated as Pi day since the date matches the first three digits of the decimal expansion of pi. 

Conclusion

In this article, we learned about irrational numbers. An irrational number is a number that cannot be expressed in the form of a fraction or ratio. To read more such informative articles on other concepts, do visit our website. We, at SplashLearn, are on a mission to make learning fun and interactive for all students. 

Solved Examples

1. Find two irrational numbers between 3.14 and 3.2.

Solution: The decimal expansion of an irrational number is non-terminating and non-repeating. The two irrational numbers between 3.14 and 3.2 can be 3.15155155515555 . . . and 3.19876543 . . .

2. Identify rational and irrational numbers from the following numbers.

 $\sqrt{5}$, 2, $\sqrt{11}$, 3.56, 1.3333 . . ., 100, 4.5346782 . . .

Solution: 

Rational numbers:  2, 3.56, 100, 1.3333 . . .

Irrational numbers: $\sqrt{5}, \sqrt{11}$, 4.5346782 . . .

3. Add $(2 + \sqrt{3} )$ and $( 3$ $- \sqrt{3} )$. Is the sum irrational?

Solution:

 $( 2 + \sqrt{3} ) + ( 3$ $-\sqrt{3} ) = 2 + 3 +\sqrt{3} – \sqrt{3} = 5$

The sum is a rational number.

4. Compare irrational numbers $\sqrt{12}$ and $\sqrt{21}$.

Solution: Since $12 \lt 21$, we can say that $\sqrt{12} < \sqrt{21}$.

5. Which decimals are irrational numbers?Solution: The decimals that are non-repeating and non-recurring are irrational numbers.

Practice Problems

Frequently Asked Questions