Rational Numbers – Definition, Operations, Examples, FAQs

The 101 to mastering any subject is the knowledge of its lexicon. The way we combine the letters of the alphabet to make a word and then arrange words in sentences to convey our thoughts is like a natural instinct to us only because we have the knowledge of the English alphabet. So, what should be the 101 for making maths a natural instinct? The knowledge of its rudimentary unit: numbers. We teach counting using whole numbers, but one of the most important aspect of the mathematical numbers system is rational numbers, or simply put, numbers between numbers.

What Are Rational Numbers?

Rational numbers are numbers that can be written in the form pq, where p and q are integers and q≠0. The difference between rational numbers and fractions lies in the fact that fractions cannot have negative numerator or denominator. Hence, the numerator and denominator of a fraction are whole numbers (denominator ≠ 0), whereas in the case of rational numbers, the numerator and denominator are integers.

Examples of Rational Numbers

• $\frac{4}{5}$, $\frac{-10}{15}$, $\frac{9}{-17}$, $\frac{-2}{-7}$

• Zero is a rational number as it can be written as  $\frac{0}{10}$, $\frac{0}{2}$, $\frac{0}{-15}$, $\frac{0}{27}$, etc. 

So, zero can be expressed as a fraction with a non-zero denominator.

• Every natural number is a rational number.

1 = $\frac{1}{1}$, 5 = $\frac{5}{1}$, 8 = $\frac{8}{1}$

So, every natural number can be expressed as a fraction with 1 as the denominator.

• Every integer number is a rational number.

-7 = $\frac{-7}{1}$, -13 = $\frac{-13}{1}$ 

So, every integer number can be expressed as a fraction with 1 as the denominator.

• Every fraction is a rational number.

$\frac{2}{3}$, $\frac{18}{7}$, $\frac{19}{11}$

Where the numerator and denominator are whole numbers and the denominator is not equal to zero.

• Positive rational numbers

A rational number is positive if its numerator and denominator have the same signs (either both positive or both negative).

$\frac{-5}{-6}$, $\frac{7}{12}$, $\frac{-19}{-12}$, $\frac{42}{85}$ 

• Negative rational numbers

A rational number is negative if its numerator and denominator have opposite signs (one of them is positive and the other is negative).

$\frac{-32}{43}$, $\frac{27}{-63}$, $\frac{-12}{14}$, $\frac{9}{-16}$

• Decimals: 0.45, 0.5446, 0.01864. Since decimals can be written as fractions with denominator as 10, 100, 1000 … decimal numbers also considered rational numbers.

Non-Examples of Rational Number

• The square root, cube roots, etc., of natural numbers if their exact value cannot be determined.

$\sqrt{2}$, $\sqrt{3}$, $\sqrt[2]{8}$, $\sqrt[3]{81}$, $\sqrt[4]{27}$ 

• $\sqrt{3}$, – $\sqrt{5}$, 8 + $\sqrt{10}$, $\sqrt{2}$ + $\sqrt{3}$

Standard Form of Rational Numbers

A rational number, $\frac{p}{q}$,  is said to be in standard form if the numerator and the denominator (p and q) have no common divisor (or factor) except 1 and the denominator “q” is positive.

How to convert a rational number into standard form:

• Consider the rational number $\frac{18}{–24}$; 

Let’s see how we can convert this rational number into its standard form.

Step 1: Make sure that the denominator is positive. If not, multiply the numerator and the denominator by “–1” to change the sign.

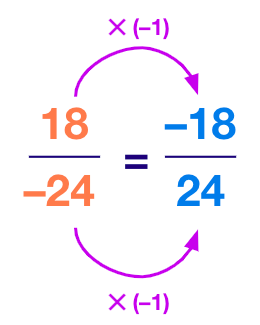
Step 2: Find all the common divisors of the numerator and the denominator.
            Here, 18 and 24 have common divisors 1, 2, 3, 6.

Step 3: Divide the numerator and the denominator by their greatest common divisor. Like this:

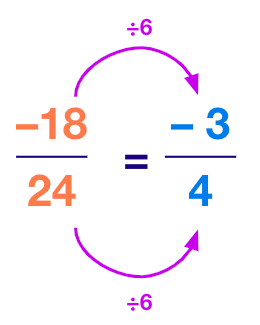
No Step 3 required! As you can see $\frac{–3}{4}$  is a standard rational number and is the standard form of $\frac{18}{–24}$.

• Consider the decimal number 0.5

Step 1: To convert a decimal number into a standard rational number, we first convert it into a rational number.

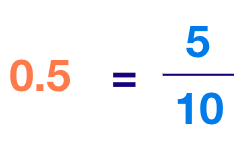
Step 2: Now follow the same steps for converting a rational number into its standard form as defined above and we get

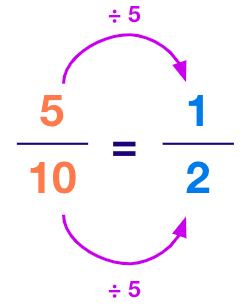
Operations on Rational Numbers 

Addition of Rational Numbers:

• When the denominators of the given rational numbers are equal:

Add the numerators and keep the denominators the same.

For example, we can add two rational numbers 2/8 and ⅜ like this:

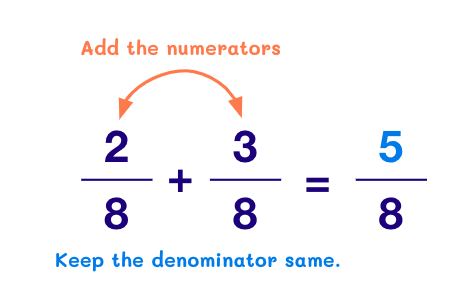
• When the denominators of given numbers are unequal:

For example, to add the rational numbers ⅖ and ¾ 

Step 1: Find the LCM of the denominator of the given rational numbers. Here, the LCM of 4 and 5 is 20.

Step 2: Convert each rational number into an equivalent rational number with the LCM as the new denominator.

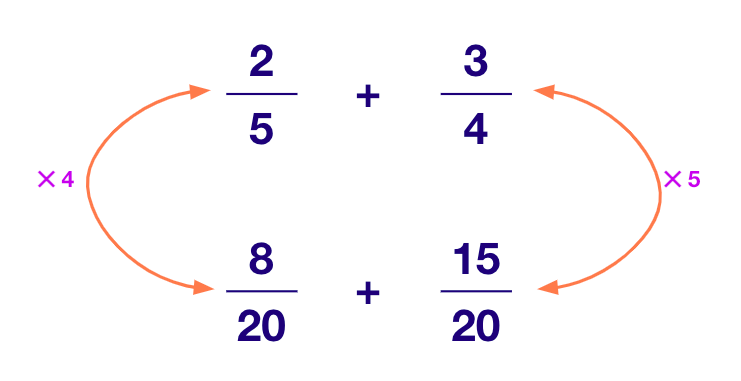
Step 3: For these new rational numbers, add the numerators and keep the denominators the same and that will be the final answer.

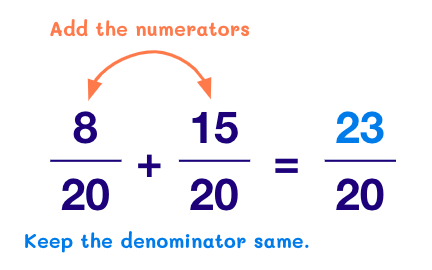
Therefore, ⅖ + ¾ = 23/20.

Subtraction of Rational Numbers:

• When the denominators of the given numbers are equal:

Subtract the numerators and keep the denominator the same.

For example:

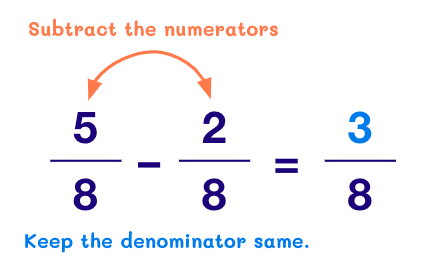
• When the denominators of the given numbers are unequal:

For example, to subtract ⅓ from ½ 

Step 1: Find the LCM of the denominator of the given rational numbers. In this case, the LCM of 2 and 3 is 6.

Step 2: Convert each rational number into an equivalent rational number with the LCM as the new denominator.

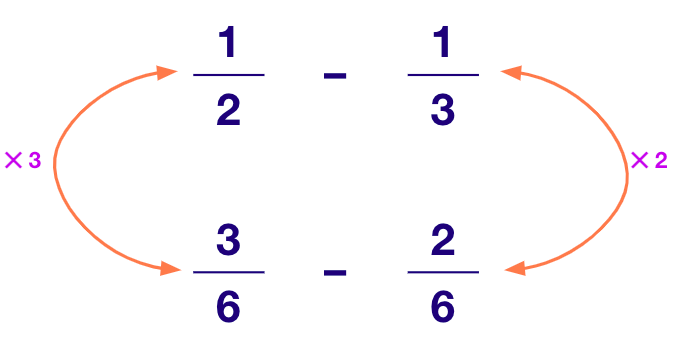
Step 3: Follow the steps of subtraction of rational numbers with equal denominators.

Therefore, ½ – ⅓ = ⅙ 

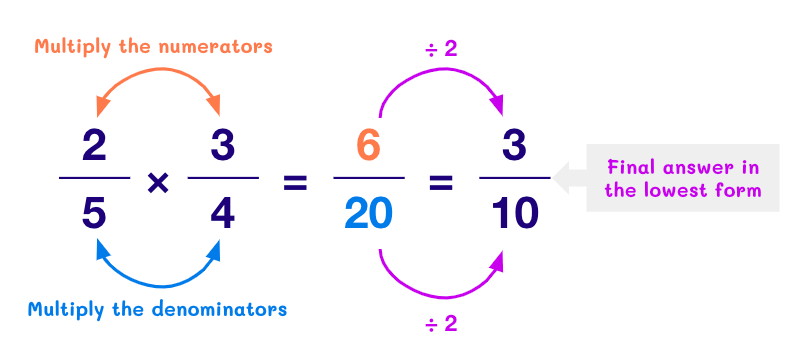
Multiplication of Rational Numbers:

This is perhaps the easiest operation on rational numbers.

To multiply two rational numbers, simply multiply the numerator and denominator of the first rational number with the numerator and denominator of the second rational number respectively.

For example, to multiply the rational numbers ⅖ and ¾, 

Solved Examples On Rational Numbers

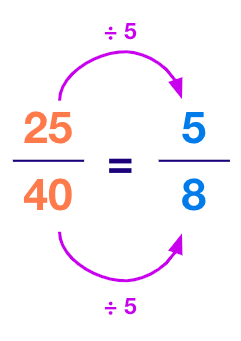
Example 1: Express $\frac{25}{40}$ in standard form.

Solution:

Greatest divisor of 25 and 40 = 5

Example 2: Add:  $\frac{2}{11}+\frac{7}{11}$.

Solution:

$\frac{2}{11}+\frac{7}{11}= \frac{2+7}{11}=\frac{9}{11}$ 

Example 3: Subtract $\frac{5}{7}$ from $\frac{9}{7}$.

Solution:

$\frac{9}{7}–\frac{5}{7}= \frac{9–5}{7}=\frac{2}{7}$

Practice Problems On Rational Numbers

Rational Numbers Attend this Quiz & Test your knowledge. 1 The number 398 can be expressed as a rational number as: 398/1 0/398 1/398 398 is not a rational number. CorrectIncorrect Correct answer is: 398/1 Whole numbers can be expressed as rational numbers with denominator 1. 398 = $\frac{398}{1}$ 2 The number 0.7 can be expressed as a rational number as: $\frac{10}{7}$ $\frac{7}{10}$ $\frac{0.7}{10}$ 0.7 is not a rational number CorrectIncorrect Correct answer is: $\frac{7}{10}$ Removing the decimal point we can represent $\frac{7}{10}$ as 0.7 3 Standard form of the number $\frac{–20}{15}$ is: 1 $\frac{2}{5}$ $\frac{-10}{3}$ $\frac{3}{-10}$ CorrectIncorrect Correct answer is: $\frac{-10}{3}$ Greatest common divisor of 20 and 15 is 5; so dividing both the numerator and denominator in –20/15 by 5 gives us –10/3. 4 Product of $\frac{8}{9}$ with $\frac{9}{8}$ is: $\frac{64}{81}$ 1 $\frac{72}{81}$ 0 CorrectIncorrect Correct answer is: 1 $\frac{8}{9}\times \frac{9}{8}=\frac{8×9}{9×8}= \frac{72}{72}$ = 1

Frequently Asked Questions On Rational Numbers