Standard Form – Definition with Examples

What is Standard Form?

Did you know that Earth is 4,543,000,000 years old? We know you skipped past all those zeroes, so we will give you a simpler way of saying it: Earth is 4.543 billion years old. Do you see how reading numbers a certain way makes them easier to understand? That’s why all the mathematicians in the world decided to agree on some rules on writing mathematical concepts so that it is convenient for everyone to read, write, and work with. This particular way is called the standard form.

All of the things you see in math, like numbers or fractions or equations or expressions, have a standard form defined for them. We can think of the standard form as the most common way of representing a mathematical element. 

Let’s look at the standard form of some common mathematical elements:

Whole Numbers

You can define the standard form of a whole number as follows.

Any number that we can write as a decimal number, between 1.0 and 10.0, multiplied by a power of 10, is said to be in standard form.

For example, take the number 123,000,000; an easier way of writing this number is ​​

1.23 × 10⁸;

If you observe carefully, 1.23 is a decimal number between 1.0 and 10.0 and so we have the standard form of 123,000,000 as 1.23 × 10⁸.

Examples of Standard Form of Numbers

• 14,300,000 in the standard form is 1.43 × 10⁷.
• 3000 in the standard form is 3 × 10³.
• Some other examples are 1.98 ✕ 10¹³ and  0.76 ✕ 10¹³.

Factoid: “Standard Form” is also called “Scientific Notation” depending on the mathematical lingo of the country you are in. In the United Kingdom and the countries that follow the same conventions as the United Kingdom, the term “Scientific Notation” is most commonly used whereas in countries that follow the US conventions majorly refer to this form of writing as the “Standard Form”.

Example 1: Consider the number 81,900,000,000,000.

Step 1: Write the first number: 8.

Step 2: Add a decimal point after this and write the remaining non-zero numbers: 8.19

Step 3: Now count the number of digits after 8. There are 13 digits. This 13 will be the power of 10 while writing the given number in standard form.

Step 4: So, in standard form: 81,900,000,000,000 is 8.19 × 10¹³.

Real-Life Examples of Standard Form

• The distance between the Sun and Mars is 141,700,000 miles or 228,000,000 km.

         This distance can easily be written in standard form as:
1.417 × 108 miles or 2.28 × 108 km.

• Atoms are tiny units of matter composed of three fundamental particles—proton, neutron, and electron.
  A proton and a neutron weigh equally, 1.67 × 10–27 kg.
  The weight of an electron is 9.11 × 10–31 kg.

Many other quantities, such as the size of planets, the size of microorganisms, the size of microchips, and the country’s population are all expressed in standard form.

Fractions

A fraction is said to be in standard form when both the numerator and denominator are co-prime numbers.

Factoid: Two numbers are said to be co-prime when their only common divisor(or factor) is 1. For example, 2 and 3, 4 and 9, 6 and 13. By virtue, two prime numbers are always co-prime.

For example, the fraction  ⅚  is a standard fraction because the numerator 5 and denominator 6 do not have only 1 as their common divisor, whereas the fraction 4/8 is not a standard fraction because the numerator and denominator have common divisors other than 1, i.e., 2 and 4.

But no worries, do you want to turn a fraction into its standard form? We got your back.
Let’s look at an example.

Consider the fraction 12/20.

Step 1: Find all the common divisors of the numerator and the denominator.
            In this case, 12 and 20 have common divisors: 1,2,4.

Step 2: Divide the numerator and denominator by their greatest common divisor. Like this:

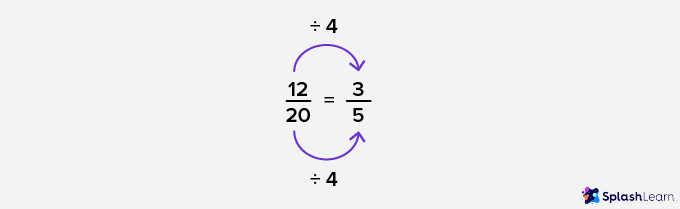
No Step 3 is required! As you can see ⅗ is a standard fraction and is the standard form of 12/20.

Examples of Standard Form of Fractions

• The most famous standard fraction is 22/7, also called “pi”.
• All unit fractions, i.e., fractions with numerator 1 are standard.

Decimal Numbers

The definition for the standard form of decimal numbers is the same as that of whole numbers,

Any number that we can write as a decimal number, between 1.0 and 10.0, multiplied by a power of 10, is said to be in standard form.

The scoop about the standard form of decimal numbers lies in their steps. This is a bit different from whole numbers, where you may have noticed, the power of 10 was a positive number like in 1.23 × 10⁸.

Let’s see how we can convert a scary-looking decimal number into a pretty-looking decimal number.

Consider the decimal number 0.0004789.

Step 1: Make your decimal number jump from its original position and place it after the first non-zero digit: 4.789.

Step 2: Count the number of digits you jumped. In this case, we jumped 4 digits. This number will be the power of 10 while writing our decimal number in standard form.

Step 3: If you have made jumps in the direction to the right, the power of 10 will be negative. If you made the jumps in the direction to the left, the power of 10 will be positive.

Step 4: So, in standard form: 0.0004789 is 4.789 × 10^-4.

Using the same method, the standard form of the decimal number 981.23 will be 

9.8123 × 10².

The standard form of mathematical elements allows us to work in a convenient and efficient manner by making them easily readable for everyone. There is no shortcut to finding the standard form of anything, but here are a few tips and tricks that we have summarized for you that you must keep in mind while writing something in standard form.

Tips to Master Standard Form

• Thoroughly understand the two parts of the standard form: digits and the power of 10.
• Remember that the power is negative if you have made jumps to the right and the power is positive when you have made jumps to the left while putting a decimal number in its standard form.
• Count the places you have moved the decimal point twice before writing the final answer.
• Don’t forget about the second cousin of prime numbers: the co-primes. They are the basics of putting a fraction in its standard form.

Solved Examples of Standard Form

Express 321,000,000 in scientific notation.

The scientific form of the number is 3.21 x 10⁸.

Express 0.00005432 in the standard form.

The scientific form of the number is 5.432 x 10^-5.

Write 25/40 in the standard form.

The scientific form of the given fraction is ⅝.

Practice Problems of Standard Form

Frequently Asked Questions of Standard Form