Equation – Definition, Types, Examples, Practice Problems

There are numerous ways in which one may define an equation. In its simplest form in algebra, the definition of an equation is a mathematical statement that shows that two mathematical expressions are equal. For instance, 3x + 5 = 14 is an equation, in which 3x + 5 and 14 are two expressions separated by an ‘equal’ sign. The most basic and simple algebraic equations consist of one or more variables in math. 

Example of an Equation:

4y + 2 = 18

4×2 + 3x − 28 = 0

9m = 49.5

$\frac{u}{6}$ = 8

Non examples of an Equation:

k + 7

u + w

x$^{3}$ + 5x

9t

Different Types of Equations:

Some of the math equations used in algebra are:

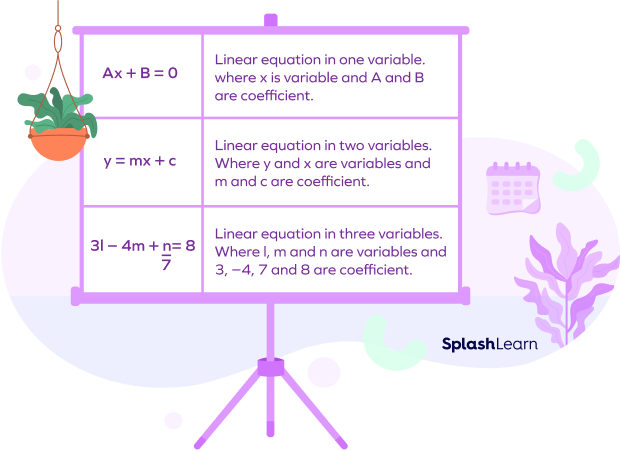
1. Linear Equation

A linear equation may have more than one variable. A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation.

2. Quadratic Equation

This is a second-order equation. In quadratic equations, at least one of the variables should be raised to exponent 2.

Example: 

ax$^{2}$ + bx + c = 0

$\frac{p^{2}}{9}$ − 1 = 0

3. Cubic Equation

This is a third-order equation. In cubic equations, at least one of the variables should be raised to exponent 3.

Example: 

ax$^{3}$ + bx$^{2}$ + cx + d = 0

a$^{3}$ – 27 = 0

4. Rational Equation

A rational equation is an equation that contains fractions with a variable in the numerator, denominator, or both.

Example:  $\frac{x}{2} = \frac{x + c}{4}$. 

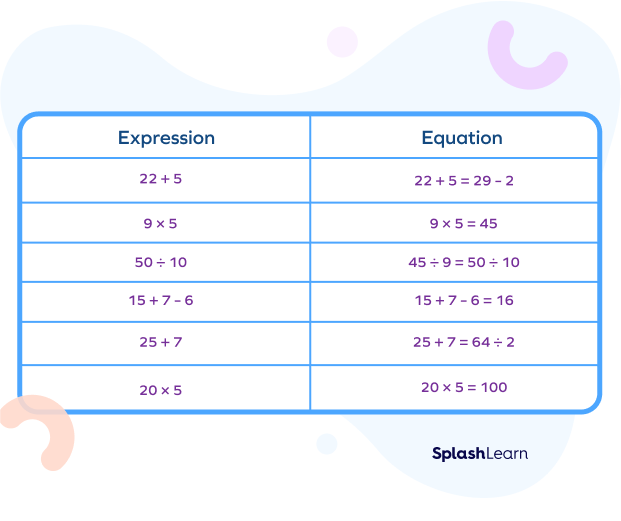
Expression vs Equation

A math expression is different from a math equation. An equation will always use an equal (=) operator between two math expressions.

For example,

What is a Solution of an Equation?

The value of the variable which makes the equation a true statement is the solution of the equation.

Example 1:

Verify that x = 3 is the solution of an equation 4x − 8 = − 5 + 3x

Substitute x = 3 in the given equation

LHS

4x − 8 = 4(3) − 8 = 12 − 8 = 4

RHS

−5 + 3x = −5 + 3(3) = −5 + 9 = 4

LHS = RHS

So,  x = 3 is the solution of an equation 4x − 8 = −5 + 3x.

Example 2:

Verify that y = −2 is the solution of an equation 2m – 4 = 1

Substitute y = −2 in the given equation.

LHS

2m – 4 = 2(−2) − 4 = − 4 − 4 = − 8

RHS 

1

− 8 ≠ 1

LHS ≠ RHS

So,  y = −2 is not the solution of given equation 2m – 4 = 1.

How to Solve Linear Equations with One Variable

• Simplify the expressions inside parentheses, brackets, braces and fractions bars.
• The same quantity can be added, subtracted, multiplied or divided from both sides of an equation without changing the equality. 

Or

Any term of an equation may be taken from one side to the other with the change in its sign. This process is called transposition.

Example:

4a – 9 = 13 – 7a

4a + 7a = 13 + 9 [transpose −7a to LHS and − 9 to RHS]

11a = 22 [add like terms]

a = $\frac{22}{11}$ [transpose 11 to RHS]

a = 2

Example:

$\frac{1}{5} + 3w = \frac{2}{5}$

3w = $\frac{2}{5} – \frac{1}{5}$ [transpose 15 to RHS]

3w = $\frac{1}{5}$

w = $\frac{1}{5\times 3}$ [transpose 3 to RHS]

w = $\frac{1}{15}$

Solved Examples On Equation

Example 1: Solve for x.

x + 8 = 12

Solution:

Here is the equation to solve: x + 8 = 12

We need to leave x alone on one side of the equation. For this, we must take 8 out of both sides.

So, x + 8 – 8 = 12 – 8

or, x = 4

Example 2: Determine if the value 3 is a solution of the equation:

4x – 2 = 3x + 1

Solution:

We will substitute the value of 3 in this equation and will check if the left-side equation is equal to the right-hand side.

So, 

4(3) – 2 = 3(3) + 1

or, 12 – 2 = 9 + 1

or, 10 = 10

Yes, 3 is a solution to the given equation.

Example 3: Solve the equation: 6(2x + 3) + x – 7 = 3(5x + 7) + 2x

Solution:

6(2x + 3) + x – 7 = 3(5x + 7) + 2x

Expanding the terms we get,

12x + 18 + x – 7 = 15x + 21 + 2x

or, 13x + 11 = 17x + 21

On further simplification,

13x – 17x = 21 – 11

−4x = 10

x = -$\frac{10}{4}$

x = -$\frac{5}{2}$

Practice Problems On Equation

Conclusion

We have thus learned the definition of the equation and its different types. Moreover, a few questions have also been solved here to give a clear idea to the students about solving an equation. A student can have a strong grip on this concept by practising such problems.Teaching maths concepts can be challenging, especially when the students are young kids. So, to make parents’ and teachers’ lives easy, SplashLearn has brought some courses specifically designed for students from K-8. After all, it should be fun to learn!    

Frequently Asked Questions On Equation