Variable in Math – Definition with Examples

What is Variables?

In real-life there are things that remain constant like your date of birth. However, there are things that vary with time and place like temperature, age, height etc. Since these quantities change they are may be called variables. 

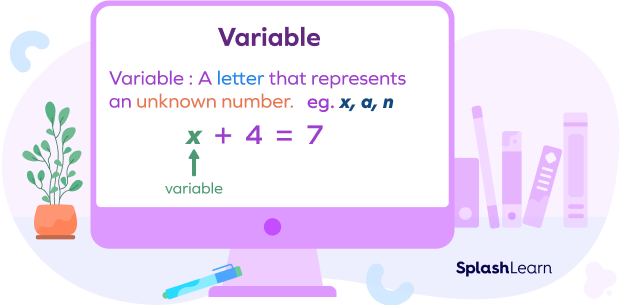
In algebra, a symbol (usually a letter) standing in for an unknown numerical value in an equation or an algebraic expression. In simple words, a variable is a quantity that can be changed and is not fixed. Variables are essential as they form a major algebra component.

We usually use “x” and “y” to express an unknown integer. However, it isn’t necessary, and we can use any letter.

Example- 
Let us take an example of the algebraic expression 2x + 6. Here, x is a variable and can take any value. If x = 1, the value of this algebraic expression will be 2(1) + 6 i.e. 8 and 

if x = 2, the value of the algebraic expression changes to 10. Hence, we can say that the value of the algebraic expression varies as the x varies. 

Now let us consider an equation 2x + 6 = 12.  

The variable x can take any value in an equation also. It may or may not satisfy the equation. If it does, it is called the solution of the equation.

Value of x	LHS 2x + 6	RHS 12
1	2(1) + 6 = 8	12
2	2(2) + 6 = 10	12
3	2(3) + 6 = 12	12

Here, x = 3 makes the equation true and is called the solution of this equation.

Different Types of Variables

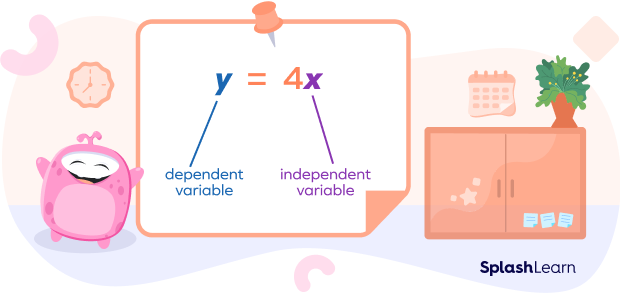
There are two types of variables: Dependent Variables and Independent variables.

Dependent Variables

The dependent variable is a variable whose value is determined by the quantity another variable takes. 

For instance, in the equation y = 2x + 3, x can take any value, like 1, 2, 3. However, the value of y will depend on the value of x. So, if x = 1, y will become 5, and if x = 2, y will become 7, and so on. Therefore, y is called the dependent variable and x is called the independent variable.

Independent Variable, x	Dependent Variable, y = 2x + 3
0	3
1	5
2	7

Independent Variables

An independent variable in an algebraic equation is one whose values are unaffected by changes. If an algebraic equation has two variables, x, and y, and each value of x is related to any other value of y, then x is an independent variable, and y is a dependent variable.

For instance, in the equation y = 2x, x can take any value. Hence, it is the independent variable in the equation.

Conclusion

Variables are a very important concept if you want to understand algebra. At SplashLearn, you will come across various resources, like games and worksheets, that will help you understand the concept of variables. The solved examples and practice problems give a step-by-step understanding, making it easier to solve sums on your own. 

Solved Examples:

1. Find one value of x that satisfies the equation 6x + 4 = 22 and one value that does not.

Solution:

Value of x	LHS	RHS
0	6(0) + 4 = 4	22	LHS $\neq$ RHS
3	6(3) + 4 = 22	22	LHS = RHS

x = 0  does not satisfy the equation as LHS is not equal to RHS.

x = 3 satisfy the equation as LHS is equal to RHS. So, x = 3 is the solution for the given equation.

2. Is h = 3, the solution of equation 7h − 2 = 12?

Solution:

7(3) − 2 = 21 − 2 = 19

19 $\neq$ 12

So, h = 3 is not a solution of a given equation.

3. What will be the value of the expression 3x + 2 when x = 4?

Solution:

3(4) + 2 = 12 + 2 = 14

Practice Problems

Variable Attend this Quiz & Test your knowledge. 1 The value of a in the equation a + 62 = 39 is 2 3 4 5 CorrectIncorrect Correct answer is: 3 3 + 62 = 3 + 36 = 39 2 Consider the equation x + y = 20. If the value of x is 14, the value of y will be 2 5 6 10 CorrectIncorrect Correct answer is: 6 14 + 6 = 20 3 Which of the following equation has y = 3 as a solution? y - 4 = 1 y + 3 = 0 2y - 5 = 2 y - 3 = 0 CorrectIncorrect Correct answer is: y - 3 = 0 3 - 3 = 0 4 A variables can take only 1 value can take only 2 values has a fixed value can take different values CorrectIncorrect Correct answer is: can take different values A variable can take any value and hence do not have any fixed value.

Frequently Asked Questions