Brackets in Math – Definition with Examples

What are Brackets?

You must have seen different symbols like these: (, ), [, ], {, and } in your math books. These symbols are called brackets. Brackets in mathematics serve a very important purpose; these symbols help us group different expressions or numbers together. Brackets imply that the thing or expression enclosed by them is to be given higher precedence over other things.

Different kinds of Brackets

In math, you will often have to use brackets while creating or solving equations. They help in grouping numbers and defining the order of operations. Generally, three kinds of brackets are used in mathematics,

• Parentheses or Round Brackets, ( )
• Curly or Brace Brackets { }
• Square or Box Brackets [ ]

Brackets always come in pairs, and if there is an opening bracket, there has to be a closing bracket. The opening brackets are (, [  and {. Their corresponding closing brackets are ), ] and }.  

Parentheses Brackets

These are also known as the round brackets and written as ( ). These are the most common types of brackets. They are used for grouping different values and equations together. Parentheses or “round brackets” are used to group terms together or specify the order of operations in an equation. 

How to Use Parentheses in Math?

1. In math, you can use parentheses in math to separate numbers. For instance, you can use them to mention negative numbers when writing an addition equation.

Here is an example to understand this better:

$3 + ( −5) = −2$

2. The second use of parentheses in math is to multiply numbers. If there is no arithmetic operation present in an equation, the presence of parentheses means you have to apply multiplication.

Let us understand this with an example:

$6 (4 + 2)$

can be written as $6 \times (4 + 2)$

Therefore, the answer is $6 \times 6 = 36$.

3. The third and final use of parentheses in math is to group numbers and define the order of operations.
4. When used simply around numbers, the round brackets denote multiplication.

For example : $(3)(4) = 12$

5. They can also be used to write negative integers in mathematical expressions.

For example $5 + ( −4) = 1$

6. Parentheses can also be used to separate out numbers from their exponents. For example: $(2)^{-3}$

Examples: $(2 + 4), 5(111), 25 − (12 + 8)$, etc.

Curly Brackets

Braces in math are symbols that are used twice, once to open “{“ and once to close “}” an argument, expression, or equation. These are commonly referred to as curly brackets and written as { }.

In general, we use braces in math for two purposes:

• For grouping a large equation, in which the second-last bracket is braces or curly brackets. For example, $7[2 + \left\{3(1 + 1) + 1\right\}]$
• For denoting a set, such as {x, y, z,…}

Like Parentheses, curly brackets are also used to group various mathematical components; however, curly brackets are also used to depict sets or to write nested expressions.  Examples: 

$[\left\{4+[3 \times ( −2)\right\}] − [\left\{(4 \times 6)+(14 \div 7)\right\} − ( −3)]$,

 $[\left\{12 − (12 − 2)\right\} + (5 − 7)] + 9$, etc.

How Do We Use Braces in Math?

Braces in math are frequently used in mathematical expressions when we have two or more than two nested groups for calculations.

So, in the first nested group, we use parentheses. In the second nested group, we use braces, and in the third nested group, we use box brackets, which contain both parentheses and braces.

For example: $3[2 − \left\{4(2 + 2) + 2\right\}]$

Here, we have three nested groups with appropriate brackets.

So, the order of solving would be:

Fun Fact: Some conventions differentiate the order of solving brackets, which is:

We will use the first convention with curly brackets in the second position throughout this article.

You need to know the BODMAS or order of operations to simplify and solve a problem.

Square Brackets

Square brackets are generally used to distinguish between sub-expressions of a complex mathematical expression.

Examples: $[100 − (3 − 1) + (7 \times 8)], 10 \times [(4 − 2) \times ( 4 \times 2)]$, etc.

Order of Operations of Brackets

When we evaluate a mathematical expression that is made up of different brackets, we have to follow certain rules. This is called the rules of operation or order of operation of brackets.

When we have a long equation for multiplication, division, addition, and subtraction, we solve each function in order to find the right answer. If the problem is solved without this order, then the chances of getting a wrong answer are high!

• The general order of operation of the bracket can be illustrated as $[ \left\{ ( ) \right\} ]$; this means that in a given problem, you would have to simplify the values in the innermost bracket first. This means that first $( )$ brackets will be solved, following which, $\left\{ \right\}$ brackets are solved and finally $[ ]$ brackets.
• The second step in solving these problems is to look for an exponent; if there is any, solve it first.
• In the third step, we look for expressions with multiplication or division operators. If both the operators are present, we check the expression from left to right. Whichever operator comes first, we solve that operator first.

For example, in the expression, $10 \times 6 \div 5$, we check from left to right, since multiplication comes first so we solve multiplication first and then division.

$10 \times 6 \div 5$ 

$=60 \div 5$

$= 12$

• In the fourth and last step, we look for numbers that need to be added or subtracted. We follow the same instruction if both the operators are present, we look from left to right in the expression, and whichever operator comes first, we solve that expression first. But if the operations are in brackets, we always solve the brackets first since brackets have the utmost precedence.

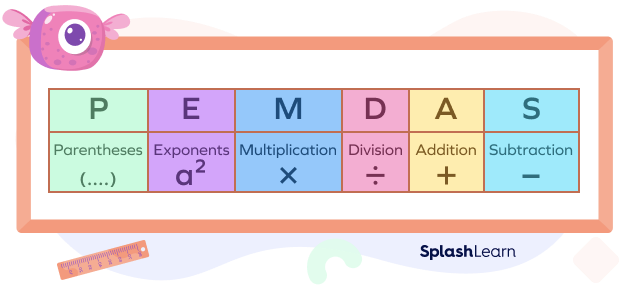
To remember the above mention steps, we can use the acronym PEMDAS,

P – Parentheses,(or brackets)

E – Exponents, (or order)

M – Multiplication 

D – Division

A – Addition

S – Subtraction.

Example 1: Let’s use pemdas to evaluate the expression 

$100 − [(3 − 1) + (7 \times 8)]$

Step 1: Solve the brackets. Follow the order of solving round brackets $( )$ first, then curly brackets $\left\{ \right\}$, and then square brackets $[ ]$.

$= 100 − [(2) + (56)]$

$= 100 − 58$

Step 2: No exponent in the given expression.

Step 3: No multiplication or division in the given expression.

Step 4: Solve the subtraction.

$= 100 − 58$

$= 42$

Example 2: While we write the order in the above form, division or multiplication and addition or subtraction hold equal importance. This means that you can either take up multiplication first or division first.

Similarly, you can take either addition first or subtraction first. The answer will be the same. So, we usually try to solve these two from left to right.

Let’s solve the above example:

$4[2 + \left\{3(1 + 1) + 2\right\}]$

First, we start with the innermost bracket (the parentheses).

$= 4[2 + \left\{3(2) + 2\right\}]$

Now, we solve the braces or curly brackets.

$= 4[2 + \left\{6 + 2\right\}]$

$= 4[2 + 8]$

Then, we solve the square brackets.

$= 4[10]$

$= 40$

In summary:

Here is the order you can follow when multiple symbols are present in an equation:

If you come across parentheses in an equation, you will first look at the terms present within them. 

Let us understand this better with an example.

Take the problem: $9 − 10 \div 5 – 3 \times 2 + 7$

Let us solve this using the order of operations you have learned.

$= 9 − 10 \div 5 – 3 \times 2 + 7$

$= 9 − 2 − 3 \times 2 + 7$ (First, you divide)

$= 9 − 2 − 6 + 7$ (Then, you multiply)

$= 7 − 6 + 7$ (Then, you subtract)

$= 1 + 7$ (Then, you subtract)

$= 8$ (And finally, you add)

Now, let us look at the same problem with parentheses: 

$9 − 10 \div (5 − 3) \times 2 + 7$

You need to calculate the numbers within the parentheses first.

$= 9 − 10 \div 2 \times 2 + 7$ (Solve the expression inside the parentheses)

$= 9 − 5 \times 2 + 7$ (Divide)

$= 9 − 10 + 7$ (Multiply)

$= −1 + 7$ (Add)

$= 6$

Did you notice? The answer to the same equation changed because parentheses were present in the equation!

Point to Remember: If there are parentheses inside other parentheses, you solve the inner expression first.

Let us understand this with an example:

Simplify the expression $(2 + (3 \times 4))$

Here, we will solve the inner bracket first.

So, the expression will become $(2 + 12) = 14$

Note that it is highly recommended to write any mathematical equation or expression with proper use of parentheses, leaving no place for ambiguity. It is important to convey the intention behind writing the math operations and indicate which operations should be carried out first.

Solved Examples

Question 1: Find the value of the expression: $(5 + 4) − (3 − 2)$.

Answer: The given expression is,

$(5 + 4) − (3 − 2)$,

Step 1: Solving the values in the brackets,

$(9) − (1)$,

Thus, the answer is $(9) − (1) = 8$.

Question 2: Find the value of the expression: $\left\{(7 − 2) \times 3\right\}  \div 5$

Answer: The given equation is,

$\left\{(7 − 2) \times 3\right\}  \div 5$

Step 1: Solving the parentheses 

$\left\{(7 − 2) \times 3\right\}  \div 5$

$= \left\{5 \times 3\right\} \div 5$

Solving the curly bracket

$= \left\{15\right\} \div 5$

$= 15 \div 5$

$= 3$

Question 3: Find the value of the expression: $(12 \div 6) \times (4 − 2)$

Solution:

The given equation is,

$(12 \div 6) \times (4 − 2)$ 

Solving the values in the brackets,

$(2) \times (2)$

Thus, the answer is $(2) \times (2) = 4$

Question 4: Find the value of the expression: $[120 + \left\{ (3 \times 4) + (4 − 2) − 1 \right\} + 20 ]$

Answer: Following the PEMDAS rule, first, 

Step 1: We solve the values in ( ) brackets,

$[120 + \left\{ (3 \times 4) + (4 − 2) − 1 \right\} + 20 ]$

$= [ 120 + \left\{ (12 ) + ( 2 ) − 1 \right\} + 20 ]$,

Now we solve the values inside the { } brackets,

$= [ 120 + \left\{ 13 \right\} + 20 ]$,

Finally, add all the values in the [ ] bracket,

The answer is 153.

Example 5: Simplify the expression: $(2 + 4 \times 6) − 4 + (2 \times 3)$

Solution: Start by solving the expressions inside the parentheses.

$= (2 + 24) − 4 + 6$ (Multiply inside the parentheses)

$= 26 − 4 + 6$ (Solve the terms inside the parentheses)

$= 22 + 6$ (Add)

$= 28$

Example 6: Simplify the expression: $( 2 \times (7 − 5)) − ((6 \div 3) + 4)$

Start by solving the innermost parentheses

$= (2 \times 2) − (2 + 4)$

$= 4 − 6$

$= − 2$

Example 7: Simplify the expression: $2 (3 + 5) + 8 (4 − 1)$

First, solve the expressions within the parentheses.

Here, the parentheses also denote a multiplication sign.

$= 2 \times 8 + 8 \times 3$

$= 16 + 24$

$= 40$

Example 8: If you have to solve the following equation, how will you proceed?

$2[1 − \left\{2(2 + 2) + 2\right\}]$

Solution: We solve the parentheses first:

$= 2[1 − \left\{2(4) + 2\right\}]$

$= 2[1 − \left\{8 + 2\right\}]$

Now, we solve the braces:

$= 2[1 − \left\{10\right\}]$

Finally, we solve the square brackets:

$= 2[ −9]$

$= −18$

Example 9: How would you solve the following equation?

$4\left\{5(4 + 2) + 1\right\}$

Solution: First, we solve the parentheses:

$= 4\left\{5(6) + 1\right\}$

Now, we need to solve the curly brackets. But within these brackets, we have to solve multiplication and addition.

So, we multiply first and then add:

$= 4 \left\{30 + 1\right\}$

$= 4 \left\{31\right\}$

Finally, we multiply 4 with the value inside the braces:

$= 124$

Example 10: What is the process you will follow to solve an equation with more than one parentheses?

$20 \div \left\{1(2 + 2) + (3 + 3)\right\}$

Solution: We will start by solving the equations within the parentheses:

$= 20 \div \left\{1(4) + (3 + 3)\right\}$

$= 20 \div \left\{1(4) + (6)\right\}$

Now, we have to solve the equation within the braces, but we have multiplication within the curly brackets, so we will solve that first:

 $= 20 \div \left\{4 + (6)\right\}$

$= 20 \div \left\{10\right\}$

$= 2 \div 1$

$= 2$

Practice Problems

Frequently Asked Questions