Exponent – Definition with Examples

Definition of Exponent

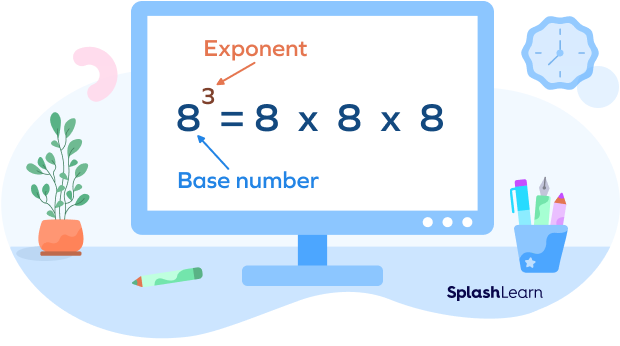
The exponent of a number indicates the total time to use that number in a multiplication. For example, 8 × 8 × 8  can be expressed as 8³ because 8 is multiplied by itself 3 times. Here, 3 is the ‘exponent’ or ‘power’ which tells how many times 8 is multiplied by itself, and 8 is the ‘base’ which represents the number being multiplied. In short, power or exponent indicates the number of times a number needs to be multiplied by itself. Here, the base can be any integer, fraction or decimal. The exponent can also take up any value, be it positive or negative.

Examples of Exponent

Here are some examples:

• 5⁴ = 5 × 5 × 5 × 5 = 625 
• 3⁵ = 3 × 3 × 3 × 3 × 3 = 243
• 14² = 14 × 14 = 196
• (−4)³ = (−4) × (−4) × (−4) = −64
• $\left(\frac{1}{2} \right)^{4}$ = $\left(\frac{1}{2} \right)\times \left(\frac{1}{2} \right)\times \left(\frac{1}{2} \right)\times \left(\frac{1}{2} \right)$ =  $\frac{1}{16}$
• (0.2)³ = 0.2 × 0.2 × 0.2 = 0.008

How to Read Numbers with Exponents

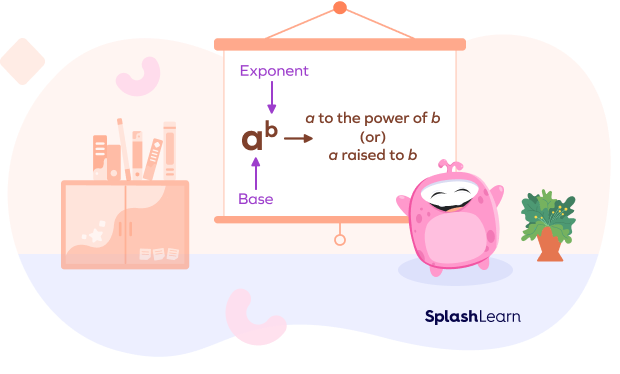
$x^{n}$ can be read in many ways.

• x to the power of n
• x raised to n
• x to the n
• x to the nth power

There are some special cases:

$x^{2}$ is also read as x square and $x^{3}$ is also read as x cube.

Properties of Exponent 

The rules or properties of exponents are used widely to solve various problems. Let us learn about them one by one: 

1. Law of product 

As per the law, to find the product of exponential expressions with the same base we add the exponents. It is given as: 

 a^m × aⁿ = a^{m + n}, where m and n are real numbers

2. Law of quotient 

As per the law, to divide two exponential expression with the same base we subtract the exponents. It is given as:

 $\frac{a^{m}}{a^{n}}$ = a^{m – n}, where m and n are real numbers and a is a non-zero term.

3. Law of negative exponent 

The negative exponent rule states that when an exponent is negative, we can convert it into positive by reciprocating it. It is represented as:

a^–m = $\frac{1}{a^{m}}$, where a is a non-zero number and m is a real number.

4. Law of zero exponent 

As per this law, if the exponent of a real number is 0, then its value is equal to 1, as

a⁰ = 1.

5. Law of power of a product 

As per this law, multiplying two different bases with the same power is equal to the product of the base with the power. For instance, 

aⁿ bⁿ = (ab)ⁿ

6. Law of power of a power 

As per this law, when the power raised to the another power of a base we multiply the exponents. It is represented as:

(a^m )ⁿ = a^mn

7. Law of power of a quotient 

According to this law, the division of different bases with the same power is represented as

a$\frac{a^{n}}{b^{n}}$ = $\left (\frac{a}{b}\right)^n$, where b is non-zero term.

Your child must be good at multiplication to solve exponents quickly, so make your child learn multiplication and various other mathematical concepts with ease through SplashLearn Worksheets and various Tutoring Courses for kids of Grades Pre-k to 5.

Fun Facts

• A base with 0 as its power is always equal to 1.
• Any number raised to power 1 is always equal to that number. 
• Any power raised to the base 0 is always equal to 0.
• The history of power or exponent is quite old. The term was used for the first time in 1544.

Solved Examples 

Example 1: Evaluate 7³ 

 Solution:

7³ = 7 × 7 × 7 = 343

Example 2: Express the result in exponential form.

2³ × 2⁴ × 2⁷ × 2

Solution:

2³ × 2⁴ × 2⁷ × 2 = 2^{3 + 4 + 7 + 1} = 2¹⁵

Example 3: Simplify $\Bigg\{\Big(\frac{2}{3}\Big)^{3}\Bigg\}^{-2}$

Solution:

$\Bigg\{\Big(\frac{2}{3}\Big)^{3}\Bigg\}^{-2}$ = $\frac{2}{3}^{-6}$ = $\frac{3}{2}^{6}$ = $\frac{729}{64}$

Example 4: Simplify the following

(i) 2¹² ÷ 2⁵

(ii) 3³ × 4³

Solution: 

(i) 2¹² ÷ 2⁵ = 2^{12 – 5} = 2⁷= 128.

(ii) 3³ × 4³ = (3 × 4) ³ = 1728

Conclusion 

In this article, we have learnt about exponents and their various laws. The exponent of a number indicates the total time to use that number in a multiplication. They are important to write the values of numbers in simplified form.
Read more about exponents and other interesting mathematical terms for children in grades Pre-k to 8 on SplashLearn. 

Practice Problems

Frequently Asked Questions