What Is Addition?
Addition is a way of combining things and counting them together as one large group.
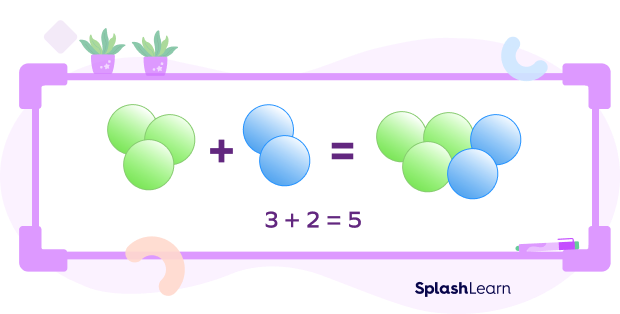
The first mathematical operation that students are introduced to in elementary mathematics is addition. To add means to bring together or combine two objects. Students then build over this understanding to learn how to add more than two numbers. In higher grades, addition is the basic element to understand more complex operations like multiplication and division.
Definition of Addition
Addition in math is a process of combining two or more numbers. Addends are the numbers being added, and the result or the final answer we get after the process is called the sum. It is one of the essential mathematical functions we use in our everyday activities. There are many situations in which we add numbers. One of the most common everyday uses for adding numbers is when we work with time or money—for example, adding up bills and receipts.
The addition has an infinite number of applications in our day-to-day life. We use addition while cooking food, while calculating bills at supermarkets, while calculating distances, and much more.
Recommended Games
Addition Symbol
The addition symbol used to indicate addition of numbers is $“+”$ (also called the plus symbol). For example, we read $5 + 3$ as $“5$ plus $3”$.
An addition sentence is a mathematical expression that shows two or more values added together and their sum. The two or more values that are added are called addends. The parts of addition sentence are two or more addends, plus symbol(s), equal sign, and the sum.
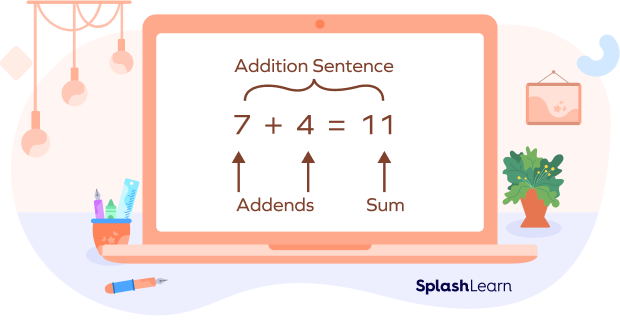
Let’s look at this with the help of another example.
Let’s say we have two yellow stars,

and three purple stars.

In order to find the total number of stars we have, we count all the stars together. That is, together we have 5 stars.
Mathematically, we write this as
$2 + 3 = 5$
Here, “+” denotes addition. The total that we get on adding two or more numbers is also called the sum. Therefore in this example, 5 is the sum of 2 and 3.
Considering one more example, if we add the numbers 6 and 4, we get the sum 10; and we write this as
$6 + 4 = 10$
Recommended Worksheets
Solve Addition Problem
We can add two numbers easily using the various methods discussed below. These methods are more convenient for adding small numbers.
In their quest to master addition, students start by learning how to add one-digit numbers using their fingers or the number line and then move on to adding bigger numbers using place value or column method. Let’s learn about the addition of two numbers: using fingers, on a number line, using the number grid, by counting forward.
Using Fingers
Addition of small numbers can be done using your fingers.
Example 1: Let’s say we have to add the numbers 5 and 2. Show 5 fingers on one hand and 2 on the other. Count the total number of fingers to find the sum.
Similarly, to add 2 and 2, show 2 fingers on one hand and 2 on the other. The sum is 4 since four fingers are shown in total.
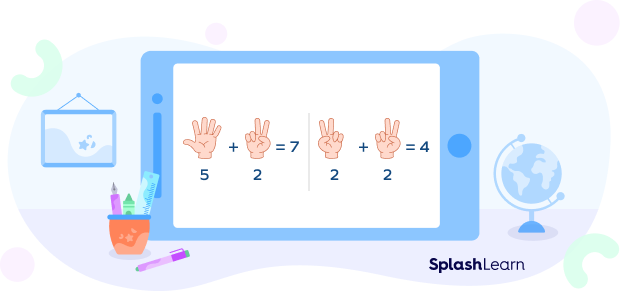
Example 2: Let’s add the numbers 5 and 3.
Step 1: Show 5 fingers on one hand and 3 on the other.

Step 2: Start counting the fingers together like this to find the total.
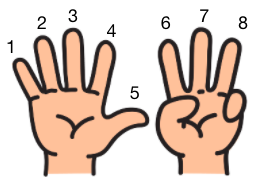
And we have our total
$5 + 3 = 8$.
Using The Number Line
We can use the number line to add. Let us look at the following addition example.
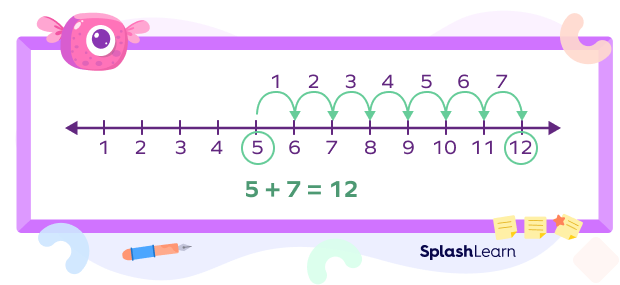
Example 1: To add 5 and 7, we can count forward 7 steps from 5, as shown below.
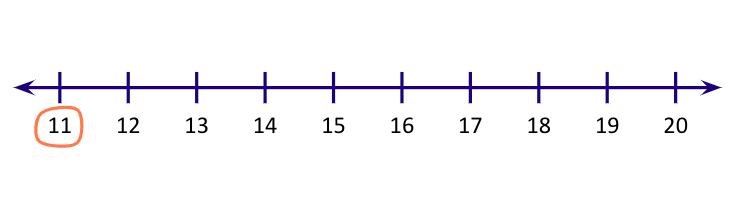
Example 2: Let’s see how we can add the numbers 11 and 3 using a number line.
Step 1: Mark the bigger number on the number line.
Step 2: Jump forward as many times as the second number.
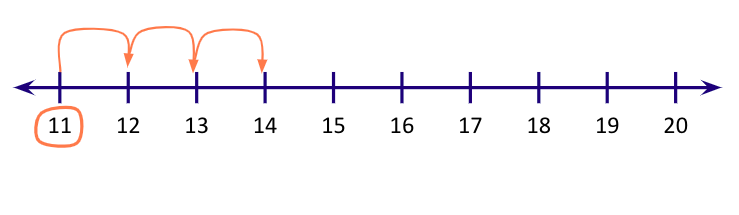
So, we have
$11 + 3 = 14$.
Using The Number Grid
Number chart is another way to add numbers.
Example: Add 57 and 16 using a hundred grid.
| Step 1: Locate the bigger number (57).Step 2: If the number to be added (16) is more than 10, break it into tens and ones. $16 = 10 + 6$. Step 3: Jump as many 10s as in the second number.$57 + 10 = 67$ Step 4: Move forward as many ones as in the second number.$67 + 6 = 73$.The number reached is the answer. So, $57 + 16 = 73$ | 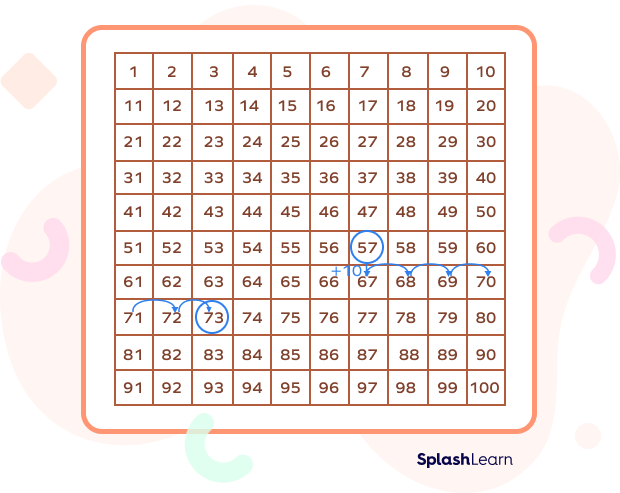 |
By Counting forward
Let’s use another example to see how this strategy works. Let’s say we have to add the numbers 5 and 4.
Step 1: Keep the bigger number in mind. In this case, 5.
Step 2: Count forward as many times as the second number i.e., 4 times.
Like this: $→ 6 → 7 → 8 → 9$.
We get 9.
So, 4 added to 5 is 9 or the sum of 5 and 4 is 9.
Vertical Addition or Column Method
While solving the problem, we can add the numbers vertically. Here, we arrange the numbers vertically using their respective place values, like ones, tens, hundreds, thousands, etc. We start adding from the right side (or digit at ones or unit place). While solving such problems, we may come across some cases with regrouping and some without regrouping. Let us understand with the help of examples.
Addition without Regrouping
Example 1: Add 41 and 26.
| Step 1: Write the numbers one below the other as per the places of the digits. | 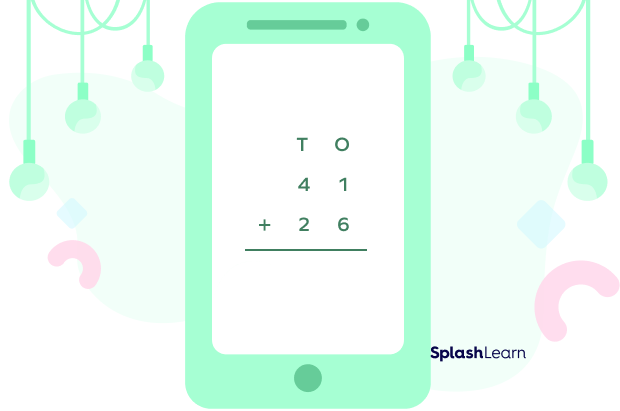 |
| Step 2: Start adding from the digits in ones place $(1 + 6 = 7)$. Write the sum under the ones digit. | 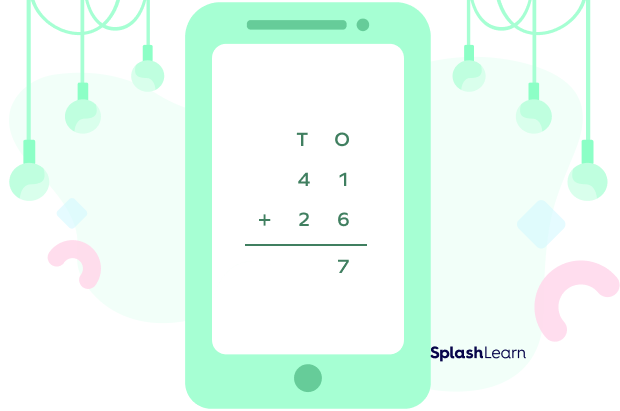 |
| Step 3: Add the tens digits $(4 + 2 = 6)$. | 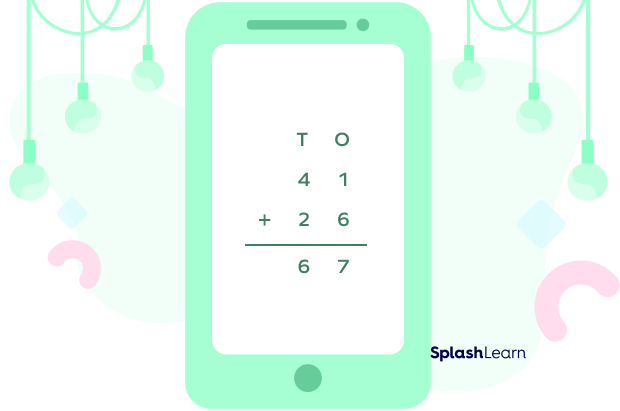 |
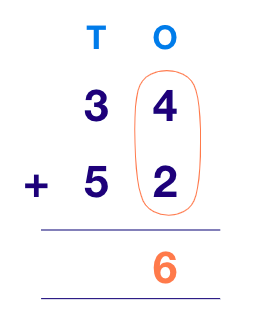
Example 2: Let’s add the numbers 34 and 52.
Step 1: Write the numbers one below the other as per their place value like this:

Step 2: Start from the right and add the digits in the ones column first.
Step 3: Move on to the next column and add the digits in the tens column.
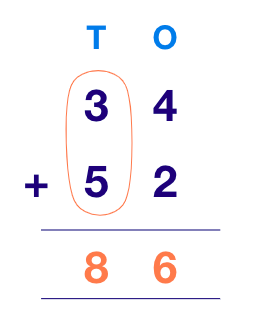
And so we have our answer:
$34 + 52 = 86$
Addition with Regrouping
This is the aspect that comes into play when the sum of the digits in any column exceeds 10.
Example 1: Add 57 and 16
| Step 1: Write the numbers below the other as per the places of the digits. | 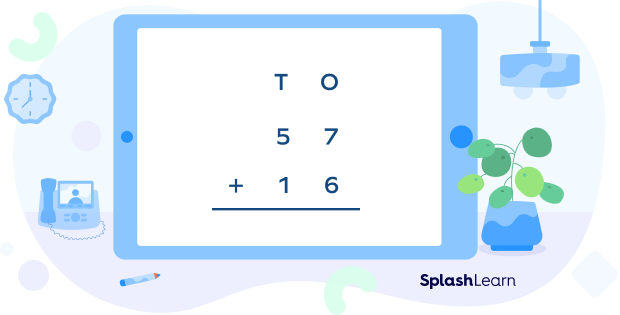 |
| Step 2: Start adding from the digits in ones place $(7 + 6 = 13)$. If the sum of the ones digit is greater than 9, write the ones digit of the sum under the ones and carry forward its tens digit to the tens column. | 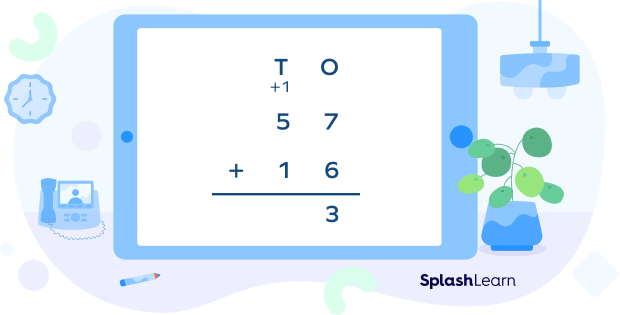 |
| Step 3: Add the tens digits. If there was a carry-forward digit, add it along. $5 + 1 + 1$ (carry-over) $= 7$ | 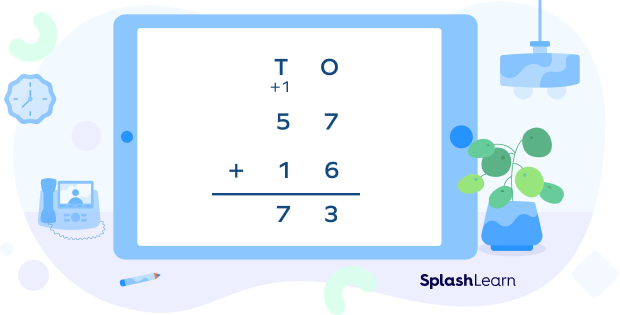 |
Example 2: Let’s try adding the numbers 29 and 46 using this method.

Step 1: Write the numbers one below the other as per their place value like this:
Step 2: As done previously, start from the right and add the digits in the ones column first. Here the sum of 9 and 6 will be 15. We think of 15 as $10 + 5$; keep the 5 in the ones column, and give the 10 as 1 ten to the tens column as a carryover.
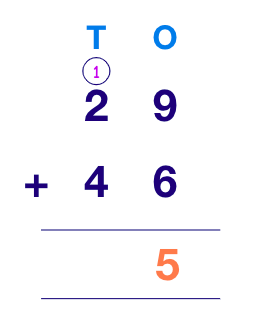
Step 3: Move on to the tens column and add the digits in this column along with the carryover digit to find the answer.
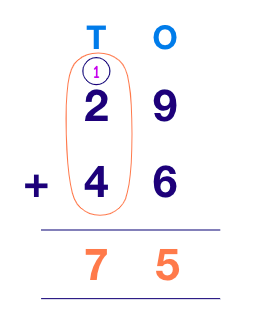
And so we have our sum: $29 + 46 = 75$
Properties of Addition
- Commutative Property of Addition
We can swap the numbers in an addition equation and the sum will remain the same.
$19 + 14 = 33$
$14 + 19 = 33$
- Identity Property of Addition
When zero is added to a number or a number is added to zero, the sum is the number itself.
$15 + 0 = 15$
$0 + 15 = 15$
- Associative Property of Addition
While adding three or more numbers, the sum of the numbers does not depend on the order in which the numbers are added. For example, we could add the numbers 5, 8 and 6 in different ways like this:
$(5 + 8) + 6 = 13 + 6 = 19$
$5 + (8 + 6) = 5 + 14 = 19$
$8 + (5 + 6) = 8 + 11 = 19$
- Distributive Property
If the sum of two numbers is multiplied by a third number, then the product is equal to the sum of the products obtained when each number is individually multiplied by the third number.
Consider the example: $(2 + 3) 5$
$(2 + 3) 5 = 5 5 = 25$
$(2 + 3) 5 = (2 5) + (3 5) = 10 + 15 = 25$
Fun Fact
- Adding zero to a number gives the number itself.
- Adding 1 to a number gives the successor of that number.
- Changing the order of the addends does not change the sum.
For example, $5 + 3 + 2 = 5 + 2 + 3 = 10$
Conclusion
Adding numbers is a fundamental mathematical process that combines two or more numerical values. We use this operation in our daily lives; some easy examples are calculating money, calculating time, counting students in a class, etc. The symbol of this operation is a ‘+’ (plus sign). Visit SplashLearn to learn more math facts.
Solved Examples on Addition
Question 1: What is the sum of the first 10 odd numbers?
Solution:
The first ten odd numbers are 1, 3, 5, 7, 9, 11, 13, 15, 17, 19.
The sum of the first ten odd numbers
$= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19$
$= 100$
Question 2: If a bag has 5 balls and 4 more balls are added to it, how many balls are there in the bag?
Solution:
Originally, there were 5 balls in the bag. Now 4 more balls have been added.
The number of balls in this bag is now $5 + 4 = 9$.
Therefore, the bag has 9 balls.
Question 3: The present age of Manny is 7 years. What will be his age after 10 years?
Solution:
Current age of Manny is 7 years.
To find Manny’s age after 10 years, add 10 to his current age.
After 10 years, his age would be $7 + 10$ or 17 years old.
Question 4: Samantha bought a bag for $214 and some books for $\$149$. How much did she spend on both?
Solution:
To find the total cost, add 214 and 149.
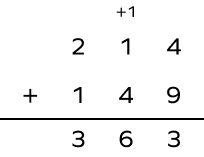
Thus, Samantha spent $\$363$ in all.
Question 5: Add 56 and 11 using the column method.
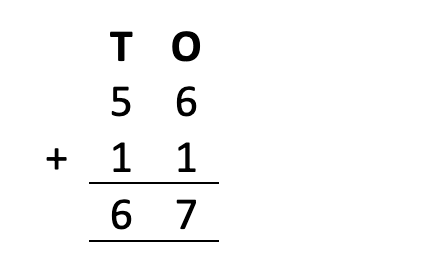
Solution:
Question 6: Add 4 and 6 on the number line.
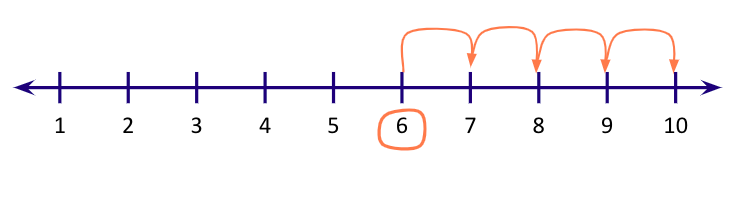
Solution:
$4 + 6 = 10$
Question 7: Find the missing number in $7 + \underline{} = 9$
Solution: $7 + 2 = 9$.
Question 8: Add and write the total number of fingers.

Solution: $2 + 5 = 7$.
Question 9: An overhead tank A has 345 gallons and another tank B has 248 gallons of water. What is the total amount of water in both the tanks?
Solution:
Amount of water in overhead tank A $= 345$ gallons
Amount of water in overhead tank B $= 248$ gallons
The total amount of water in both the tanks can be calculated by adding 345 and 248.
$345 + 248 = 593$ gallons
Question 10: There are 596 men, 632 women, and 407 children in a town. Find the total population of the town.
Solution:
Number of men $= 596$
Number of women $= 632$
Number of children $= 407$
Total population of the town is 596, 632, and 407.
We get $596 + 632 + 407 = 1635$
Practice Problems on Addition
Addition
Which of the following equations represents the total number of circles in the figure below?

There are 8 green circles and 7 blue circles, So, there are $8 + 7 = 15$ circles in all.
What is the sum of 700 and 136?
Sum of 700 and 136 is $700 + 136$ or 836.
Find the value of 4 hundreds $+ 26$ tens?
4 hundreds $+ 26$ tens $= 400 + 260 = 660$
Which of the following is the sum of the smallest and the greatest two-digit numbers?
Sum of the smallest and the greatest two-digit numbers $= 10 + 99 = 109$
1385 girls and 432 boys took part in an art competition. Find the total number of participants.
Total number of participants $= 1385 + 432 = 1817$
Which property is shown by the addition sentence $11 + 0 = 11$
The sum of any number and zero is the number itself.
Find $5 + 7 + 9$.
$5 + 7 + 9 = (5 + 7) + 9 = 12 + 9 =21$
A bouquet has 36 red roses and 18 white roses. How many roses does the bouquet have in all?
Number of red roses $= 36$
Number of white roses $= 18$
Total number of roses $= 36 + 18 = 54$
Bus A has 45 passengers, Bus B has 56 passengers and Bus C has 32 passengers. How many passengers are on Bus A and Bus C?
Number of passengers in Bus A $= 45$
Number of passengers in Bus C $= 32$
Number of passengers on Bus A and Bus C $= 45 + 32 = 77$
Frequently Asked Questions on Addition
What is addend?
Addend is the part of the statement where we add two numbers; an addend is defined as the value that is to be added to find a sum.
What is a sum?
A sum is a result when we add two or more numbers.
Why is addition important?
Adding numbers is a fundamental mathematical concept, essential for the simplest problems in our daily activities. One of the most common applications is when we work with money—for example, adding up bills and receipts.
What is meant by addition with and without regrouping?
Addition without regrouping is when the sum of the digits in each place value column is less than or equal to 9. Addition with regrouping is when the sum of the digits in at least one of the place value columns is greater than 9.
What is the zero property of addition?
The zero property of addition states that when we add any number and zero, we get the number itself. For example: 5 + 0 = 5
What is skip counting?
The method of counting forward by numbers other than 1 is defined as skip counting. For example, starting from 10 and skip counting by 5 would mean adding 5 every time to each new number we get: 10, 15, 20, 25,…
What number should be added to a number to get its successor?
1 added to a number gives the successor of the number.
If we subtract 1 from a number what number will we get?
When 1 is subtracted from a number we get a predecessor of the number.
Where do we use addition in our day-to-day life?
To find the total number of objects, bill amount, total distance traveled, etc.




































