Addend in Math

Addends – Introduction

Addends in math can be defined as the numbers that we add together to get a sum. In addition, we calculate the total or the sum of two or more numbers. 

Example:

Observe the image given below. How many apples are there in total?

There are 7 apples in one basket and 4 apples in the other. So, in order to find the total number of apples, we add 7 and 4. So, the total number of apples is $7 + 4 = 11$. Here, 7 and 4 are addends.

What is an Addend in Math?

Addend, as we just discussed, simply refers to the numbers being added together. So, for any addition equation, the individual numbers which together form the sum are addends.

Addend Definition

Addends are the numbers or terms that are added together to form the sum. 

Let’s consider an example. If 8 candies are added to the collection of 7 candies, we will get $7 + 8 = 15$ candies.

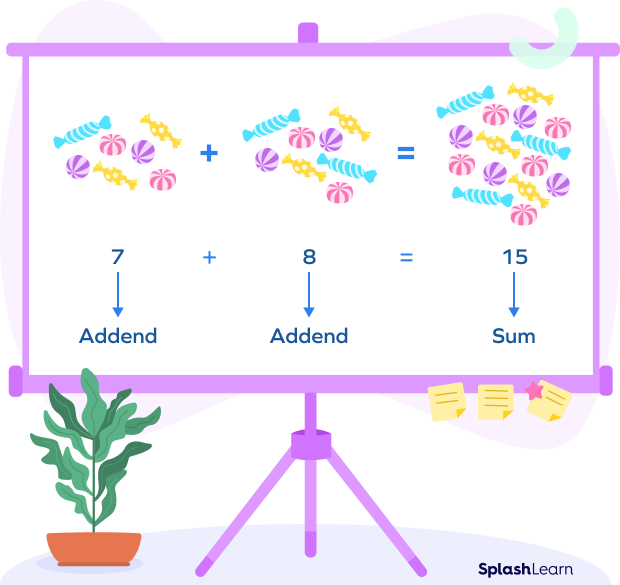
Here’s another example.

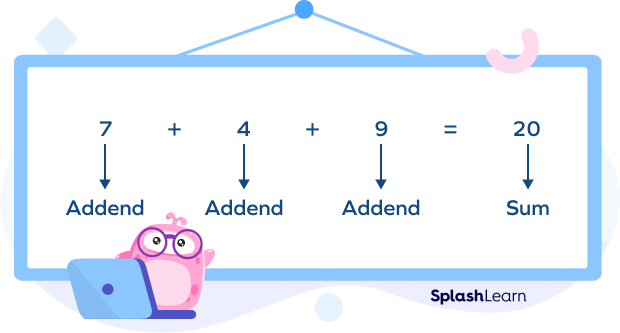
Different Forms of Addends 

Addends are not necessarily just numbers. The following examples show their different forms.

1) $128 + 55 = 183$

In this example, 128 and 55 are the addends. 

2) $3\text{x} + 5\text{y} + 6\text{z}$

Here, the addends are 3x, 5y, and 6z.

3) $2\text{yz}+6\text{x}^2\text{y}+\text{xyz}^3$

For this example, the addends are still just terms being added together: $2\text{yz}, 6\text{x}^2\text{y}$ and $\text{xyz}^3$.

Properties of Addition

Properties of addition define the different ways in which we can add the given integers. Let’s discuss a few properties of addition.

Commutative Property of Addition

According to this property, when two numbers are added, the sum remains the same even if we change their order. It can be represented as;

$\text{A} + \text{B} = \text{B} + \text{A}$

where, A and B are integers. 

For example:

Let us take $\text{A} = 12$ and $\text{B} = 7$

$12 + 7 = 19$ and $7 + 12 = 19$

Thus, $12 + 7 = 7 + 12$

The order of numbers does not matter. Hence, the addition follows commutative law. The word “commute” means switching one thing for another.

Associative Property of Addition

According to this property, when we add three or more numbers, the sum will be the same, even if the grouping of addends have changed. So, the association of numbers in different combinations does not affect the sum. We can represent this property as;

$\text{A} + (\text{B} + \text{C}) = (\text{A} + \text{B}) + \text{C}$

For example:

Let us take $\text{A} = 3, \text{B} = 5$ and $\text{C} = 7$

LHS $= \text{A} + (\text{B} + \text{C}) =  3 + (5 + 7) = 15$

RHS $= (\text{A} + \text{B}) + \text{C} = (3 + 5) + 7 = 15$

LHS $=$ RHS

$15 = 15$

In this property, we use the parentheses to group the numbers. Here, the word “associate” refers to making connections with a group of things.

Distributive Property of Addition

In this property, the sum of two numbers multiplied by the third number is equal to the sum of the products when each of the two addends is multiplied by the third number separately. We can represent this property as:

$\text{A} \times (\text{B} + \text{C}) = (\text{A} \times \text{B}) + (\text{A} \times \text{C})$

Example:

Let us take $\text{A} = 2, \text{B} = 4$ and $\text{C} = 5$

LHS $= A \times (\text{B} + \text{C})$ 

           $= 2 \times (4 + 5)$

      $= 2 \times 9$

           $= 18$

RHS $= (\text{A} \times \text{B}) + (\text{A} \times \text{C})$

 $= (2 \times 4) + (2 \times 5)$

            $= 8 + 10$

            = 18

LHS $=$ RHS

The distributive property is the combination of both the addition operation and the multiplication operation.

Additive identity Property of Addition

Addition of zero and any number is always the number itself. So, the number zero is known as the “identity” of the addition operation. It can be represented as:

$\text{A} + 0 = \text{A}$ or $0 + \text{A} = \text{A}$

For example:

$10 + 0 = 10$  and  $0 + 10 = 10$

We can remember this property using the word “identity.” The number zero when added to any number maintains the “identity” of that number and gives the sum as the number itself.

Rule of Change of Addends

When one of the addends changes by a certain amount, the sum changes by the same amount. 

For example: Consider the following equation.

$3 + 4 = 7$

If we increase the number 3 by 2, we get

LHS $= (3 + 2) + 4 = 9$

RHS $= 7 + 2 = 9$

So, the sum also increases by 2.

Fun Fact!

The opposite sides of a dice always add up to seven. Go ahead, roll and check!

Conclusion

In this article, we learned about addends. They are the numbers that are added together to form a sum. To read more such informative articles on other concepts, do visit our website. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.

Solved Examples

1. In the sum $4 + 6 + 9 = 19$, which numbers are addends?

Solution: Since we are adding 4, 6, and 9, the addends are 4, 6, and 9.

2. Find the missing number, if $15 + \underline{}= 29$?

Solution: Missing number $= 29$ $-$ $15 = 14$

3. By which property can we say that $12 + 13 = 13 + 12$?

Solution: By commutative property of addition, we have

$a + b = b + a$ for any two numbers.

Thus, $13 + 12 = 12 + 13$ holds true by commutative property of addition.

4. Use distributive property to find the value of $2(5+9)$.

Solution: By distributive property, we have 

$\text{A} \times (\text{B} + \text{C}) = (\text{A} \times \text{B}) + (\text{A} \times \text{C})$

$2 (5+9)=(25) +(29)$

                      $= 10 + 18$

                      $=28$ 

5. Find the missing addend if $23 + 62 + \underline{}= 134$.Solution: Missing addend $= 134$ $-$ $23$ $-$ $62 = 49$

Practice Problems

Frequently Asked Questions