What Is Addition?
Addition is the method of adding or summing up two osr more numbers to get the final value. The sign (+) denotes addition. The numbers that are added are called addends, and the total value is called the sum.

In the above example, 6 and 4 are addends, and 10 is the sum.
Recommended Games
Properties of Addition
The properties of addition are the rules we can follow while adding numbers. Using these properties can make the calculation more straightforward and helps to solve complex problems in Math. Let us learn more about the different properties of addition.
Recommended Worksheets
What are the Five Properties of Addition?
The five basic properties of the addition are
- Closure property of Addition
- Commutative property of Addition
- Associative property of Addition
- Additive identity property of Addition
- Additive inverse property of Addition
Closure Property of Addition
Closure property for addition states that when we add two natural numbers, we always get a natural number. The same is true for whole numbers, integers, fractions, and decimals.
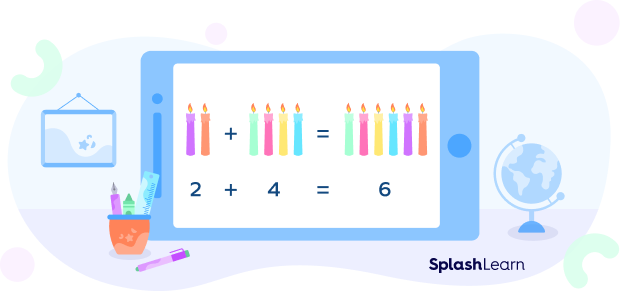
The above example shows that the sum of two natural numbers is always a natural number.
Commutative Property of Addition
When we add two or more numbers, their sum is the same regardless of the order of the addends. We can write this property in the form of A + B = B + A.
For example, 2+4=4 + 2 = 6
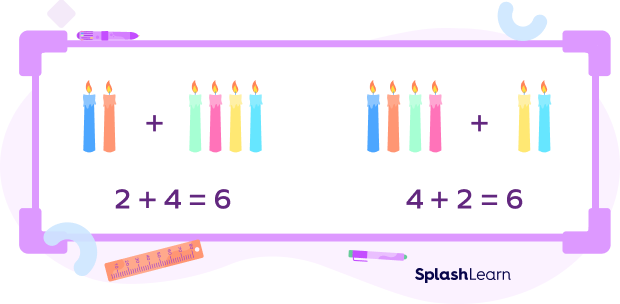
Therefore, 2+4 is equal to 4 + 2 because both sentences give a sum of 6.
This is called Commutative Property of Addition.
Associative Property of Addition
When we add three or more numbers, the sum is the same regardless of the grouping of the addends. It also means that when we add three different numbers, the result is not affected by the addition pattern followed.
A +( B+C) = (A + B)+C
For example, (4 + 2) + 3 = 4 + (3 + 2)
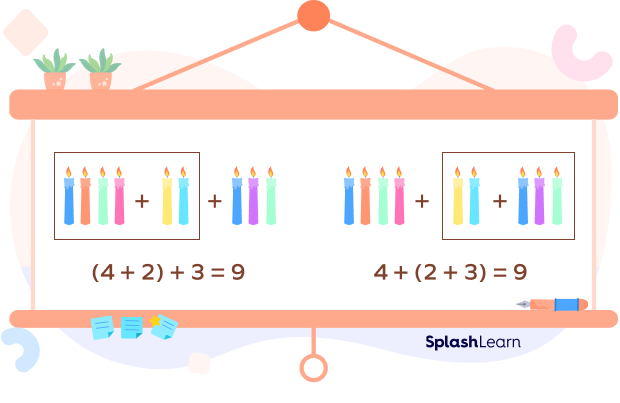
From the example we see that the sum of the three numbers will remain the same, no matter how we group them. This property is called Associative Property of Addition.
Additive Identity Property of Addition
On adding zero to any number, the sum remains the original number. Adding 0 to a number does not change the value of the number. It is true for natural numbers, whole numbers, fractions, integers, and decimals.
For example,
3 + 0 = 3
4.5 + 0 = 4.5
From the above example of the property of addition, we get that adding 0 to any number gives us the number itself. This is called the Additive Identity Property of 0.
Additive Inverse of Addition
Additive inverse of a number x is the number that, when added to x, yields zero. So, the additive inverse of a number x is –x. Therefore, we can say that the additive inverse of a number is equal but opposite in sign to it.
For example, 14 is a positive number and the additive inverse of 14 is -14.
14 + -14 = 0
For example, -5 is a negative number and the additive inverse of -5 is 5.
-5 + 5 = 0
Conclusion
In this lesson, we understood the five properties of addition. The addition properties in math make it easier to work with numbers by allowing you to regroup them so that an equation is easier to solve. Understanding the properties of addition and subtraction can help you work with numbers more effectively. You can find interesting math lessons on our platform. Learn the concepts of mathematics through enjoyable games and worksheets at SplashLearn.
Solved Examples On Properties of Addition
Example 1: Find the missing number using the property of addition.
36 + (49 + 81) = (36 + 49) + ___
Solution:
Using the associative property of addition, 36 + (49 + 81) = (36 + 49) + 81
Therefore, the missing number must be 81.
Example 2: What is the additive inverse of $-\frac{3}{2}$?
Solution:
The additive inverse of a number is equal but opposite in sign to it. So, the additive inverse of $-\frac{3}{2}$ will be $-\frac{3}{2}$.
Example 3: Fill in the blank using the property of addition.
3867 + _____ = 3867
Solution:
The sum of a number and 0 gives us the number itself
Therefore, the missing number is 0 and 3867 + 0 = 3867
Practice Problems On Properties of Addition
Properties of Addition - Definition with Examples
Which of the following property is denoted in (-3) + 4 = -1?
Explanation:
Closure property states that the addition of 2 integers is always an integer.
Which of the following property is denoted in $\frac{3}{4}$ + $\frac{1}{2}$ = $\frac{1}{2}$ + $\frac{3}{4}$ ?
Explanation:
Commutative property states that the sum of addends remains the same irrespective of the order in which they are added.
Which of the following is the additive identity of a whole number?
Explanation:
0 is the additive identity of any whole number as when we add 0 to any number, we get the number itself.
Frequently Asked Questions On Properties of Addition
How can we use properties of addition?
The properties of addition can be used to add integers, fractions, or decimals.
For example, the commutative property of addition helps us to understand that changing the order of the addends does not change the sum, therefore, numbers can be added in any order.
What is the difference between additive identity and the additive inverse of a number?
Additive inverse is added to a number to yield zero. The additive inverse of a number a is –a. Additive identity, when added to a number, gives the same number as the result. The additive identity of a number is 0.
What is the Zero Property of Addition?
The zero property of addition is another name for the identity property of addition. It states that if any number is added to 0, the sum is the number itself. For example, 835 + 0 = 835.




































