Definition:
To “associate” means to connect or join with something.
According to the associative property of addition the sum of three or more numbers remains the same regardless of how the numbers are grouped.
Here’s an example of how the sum does NOT change irrespective of how the addends are grouped.
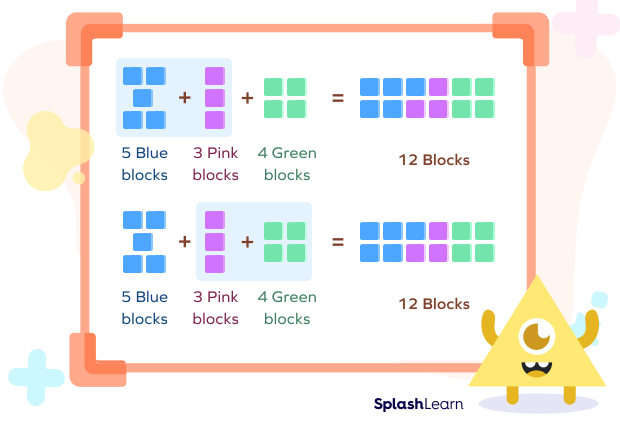
As seen in the example above, grouping is defined with parentheses. Whether we group 5 and 3 or 3 and 4 within the parentheses, the final sum is 12. You can verify the final result by checking the colored blocks that stay the same in both the cases.
General Case:
For any three numbers a,b and c
a + (b + c) = (a + b) + c

i.e. when you add, you can group the numbers in any combination.
Let us take another example to understand and prove the formula.
Let us group 14 + 7 + 5 in two ways.
- Step 1: We can group the set of numbers in two different ways as (14 + 7) + 5 or as 14 + (7 + 5).
- Step 2: Add the first set of numbers, that is, (14 + 7) + 5. This can be further solved as 21 + 5 = 26.
- Step 3: Add the second set, i.e, 14 + (7 + 5) = 14 + 12 = 26.
- Step 4: The sum of both the expressions is 26.
This shows that the sum remains the same irrespective of how we group the numbers with the help of brackets.
The minimum numbers we require for associative property of addition are 3. However, the associative property of addition holds true for more than three numbers too.
The associative property along with other properties in Mathematics are useful in manipulating equations and their solutions.
Recommended Games
Closely Related Concepts:
- The associative property holds for multiplication as well i.e. for any three numbers a, b and c, a $\times$ (b $\times$ c) = (a $\times$ b) $\times$ c
Let a = 2, b = 3, c = 4
a $\times$ (b $\times$ c) = 2 $\times$ (3 $\times$ 4) = 2 $\times$ 12 = 24
(a $\times$ b) $\times$ c = (2 $\times$ 3) $\times$ 4 = 6 $\times$ 4 = 24
Hence, a $\times$ (b $\times$ c) = (a $\times$ b) $\times$ c
- The associative property does not hold for subtraction. Let us look at an example
Let a = 2, b = 3, c = 4
a- (b – c) = 2 – (3 – 4) = 3
(a – b) -c = (2 – 3) – 4 = -53
Hence, associative property does not hold for subtraction.
- The associative property does not hold for division. Let us look at an example
a $\div$ (b $\div$ c) = 2 $\div$ (3 $\div$ 4) = 2.67
(a $\div$ b) $\div$ c = (2 $\div$ 3) $\div$ 4 = 5.97 $\neq$ 2.67
Hence, associative property does not hold for division.
Recommended Worksheets
Solved Examples on Associative Property of Addition
1. Is (5 + 10) + 4 the same as 5 + (10 + 4)?
Answer: Yes. Let’s solve and check:
(5 + 10) + 4 = 15 + 4 = 19
And, 5 + (10 + 4) = 5 + 14 = 19
If we group these three numbers differently, we get the same answers.
2. Fill in the missing numbers:
21 + (45 + 36) = (21 + 45) + _ = _
Answer: Using the associative property of addition,
21 + (45 + 36) = (21 + 45) + 36 = 102
3. Solve for x using the associative property formula: (2 + 3) + x = 2 + (3 + 6)
Answer: Given, (2 + 3) + x = 2 + (3 + 6)
According to the associative property of addition, LHS = RHS,
Hence, 5 + x = 2 + 9
Or 5 + x = 11
Or x = 6
Practice Problems on Associative Property of Addition
The Associative Property of Addition
Choose the correct option to fill the blank: $20 + (7 + 4) = (20 + \underline{} ) + 4$
Using the associative property of addition,
$20 + (7 + 4) = (20 + 7) + 4$
Which of these equations is correct?
The associative property holds for addition and multiplication only.
The property does not apply to subtraction, and hence the other equations are incorrect.
Which of the following is an example of the associative property of addition?
The associative property holds for addition and multiplication only.
The property does not apply to subtraction, and hence the other equations are incorrect.
Which of these equations is correct?
The associative property holds for addition and multiplication only. The property does not apply to subtraction, and hence the other equations are incorrect.
Conclusion
Are you a parent or a teacher? Do you want to make learning math a fun activity for your kids? Join SplashLearn, a creative and complete learning platform, for free!
Frequently Asked Questions on Associative Property of Addition
How many numbers are required to apply the associative property of addition?
A minimum of three numbers are required to apply the associative property of addition.
Does the associative property apply to subtraction?
No. The associative property applies to addition and multiplication only and not to subtraction or division.
What is the benefit of using the associative property of addition?
The associative property of addition helps you add numbers faster. Instead of adding a list of numbers in the order that they’re written, add them in any order convenient to you. In the case of a problem like 4 + 19 + 10 + 16, it would be wise to add 4 and 16 to get 20, then add 20 and 10 to get 30, and finally, add 30 and 19 to get 49.
Is there any other property of addition apart from the associative property?
Yes. There are four properties related to addition. The other three properties are commutative property of addition, additive identity of addition, and the distributive property of multiplication over addition.




































