Additive Identity Property – Definition With Examples

Additive Identity Property of Zero Definition

Additive identity property of zero states that adding 0 to any number results in the number itself. 

An additive identity is a number that when added to any other number gives the sum as the number itself. Can you guess which numbers can be called additive identities? 

Let’s find out by adding various numbers to 5: 

$5 + 3 = 8$

$5 + 2 = 8$

$5 + 1 = 6$

$5 + 0 = 5$ (Oh! we got 5 as the sum.)

Now, let’s see: If we add 0 to any other number, do we get the same number?

$6 + 0 = 6$

$10 + 0 = 10$

Clearly, if we add 0 to any number, we would always get the same number as the sum. So, zero is the additive identity.

Now, let’s see if we can find any number other than 0 that is an additive identity. Let’s do this through an example. 

Additive identity property of zero example:

A flock of 8 birds sat on the branch of a tree. After some time, the number of birds on the branch is the same, that is, 8. 

Can you think of all possible numbers of birds that might have joined the flock?

Since the number of birds remained the same, we can assume that no bird joined the flock. Clearly, the number representation for “no bird” would be 0. 

So, we can say that 0 is the only number that, when added to another number, gives the same number as the sum. 

Additive Identity Holds True for Which Number Sets? 

This property can be applied to all types of numbers, like whole numbers, real numbers, complex numbers, integers, rational numbers, fractions, decimals, integers and so on. However, additive identity cannot be associated with the set of natural numbers because 0 does not belong to the set of natural numbers. Natural numbers start from 1. Let’s verify this property for some numbers.

Additive Identity Property of 0 for Fractions

Additive identity property of 0 for fractions states that if we add a fraction to zero, it will give the same fraction as a result. Let’s model the fraction $\frac{3}{4}$ and add 0 to it. Note that we can write 0 as $\frac{0}{4}$ in the fraction form. 

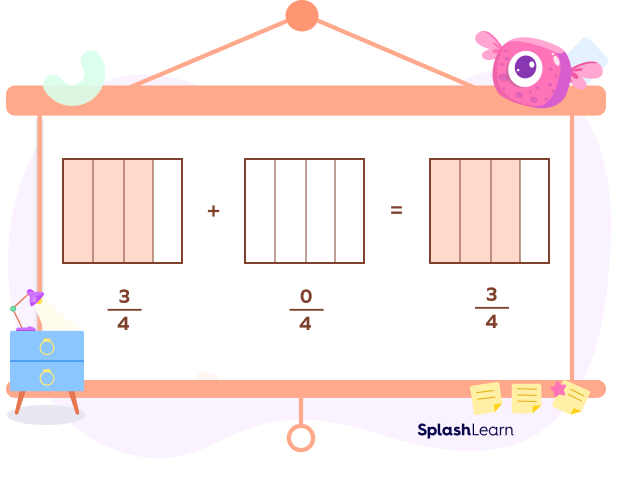
It is clear that additive identity holds true for fractions. 

Additive Identity for Decimals

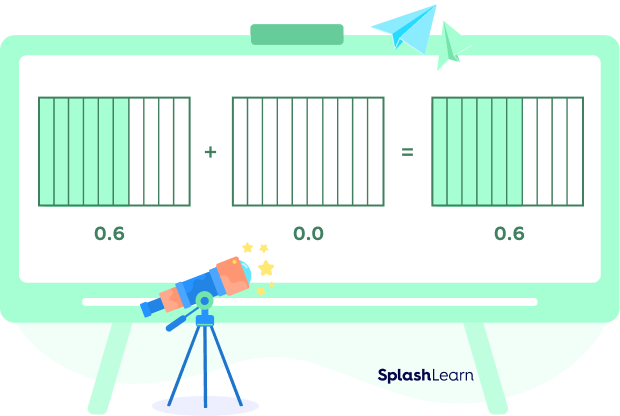
Additive identity for decimals states that if we add a decimal number to zero, it will give the decimal number itself as a result. Let’s model the decimal 0.6 and add 0 to it. Note that we can write 0 as 0.0 in the decimal form.

General form of additive identity

Suppose a is any number other than a natural number, then we can express additive identity mathematically as: 

a + 0 = a = 0 + a

Conclusion

In this article, we learned about additive identity. It is the number that, when added to another number, gives the same number. The number 0 has the additive identity property. To read more such informative articles on other concepts, do visit our website. We, at SplashLearn, are on a mission to make learning fun and interactive for all students.

Solved Examples on Additive Identity Property

1. Fill in the blank. 

$\underline{} + 0 = \frac{2}{7}$

Solution: According to the additive identity property, a + 0 = 0 + a = a, where a is any number. Here a = $\frac{2}{7}$, so the missing number is also $\frac{2}{7}$.

2. Fill in the blank. 

$( –$ $2) + \underline{} = ($ $–$ $2)$

Solution: According to the additive identity property, a + 0 = 0 + a = a, where a is any number. 

So, $( –$ $2) + 0 = ($ $–$ $2)$. 

So, the missing number is 0. 

3. There is a basket of apples. How many more apples should we put into the basket so that the count of the apples remains the same?

Solution: Since we need the number of apples to be the same, the number of apples we need to put in the basket will be 0. 

4. There is a jar of toffees. How many more toffees should we put into the jar so that the count of toffees remains the same?
Solution: Since we need the number of toffees to be the same, the number of toffees we need to put in the jar will be 0.

Practice Problems on Additive Identity Property

Frequently Asked Questions on Additive Identity Property