Addition is the first arithmetic operator that students learn about while studying elementary mathematics. Addition, as the name might suggest, is an easy topic and also lays the foundation for multiplication and some multi-digit arithmetic. One of the very interesting properties of addition is the commutative property.
Let’s take an example.
Suppose you have 3 apples and 2 oranges.
How do you find the total number of fruits you have?
You add 3 and 2, and you get 5.
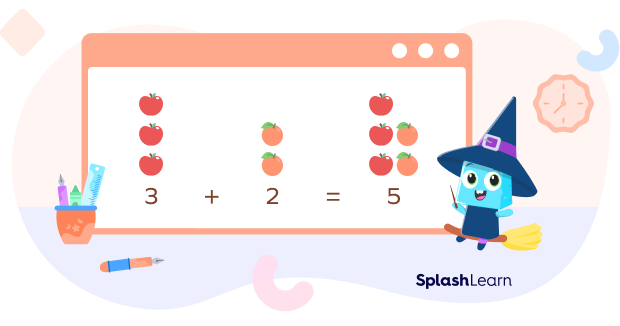
But do you think that we would have gotten a different answer if we had taken the oranges first and then the apples?
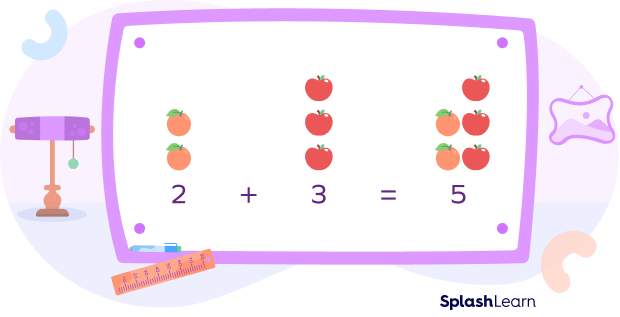
No, the total number of fruits is still the same. It’s 5.
And that is what the interesting property of commutativity for addition states.
What is Commutative Property of Addition?
To “commute” means to travel or move around. The commutative property of addition states that a change in the order of the numbers being added does not affect the sum. We can define commutative property of addition as adding the numbers in any order will give the same answer.

Here, a and b can be whole numbers, integers, decimals, or even fractions.
Commutative Property of Addition Examples:
- 15 + 16 = 16 + 15 = 31
- 4 + (–6) = (–6) + 4 = (–2)
- 0.5 + 0.6 = 0.6 + 0.5 = 1.1
- $\frac{1}{5}$ $+$ $\frac{2}{5}$ $=$ $\frac{2}{5}$ $+$ $\frac{1}{2}$ $=$ $\frac{3}{5}$
Recommended Games
Do Other Operators Also Follow the Law of Commutativity?
Not really. The law of commutativity can only be applied to the concepts of addition and multiplication.
Let’s say we want to solve the expression 3 times 4 or 3 ✕ 4.
We can simply skip count by 4 three times and we get 12.
Similarly, we can solve for the depression 4 times 3 or 4 ✕ 3, and we get 12 again.
So, changing the order of the numbers to be multiplied didn’t really change the product.
Hence, multiplication does follow the law of commutativity.
However, if we talk about subtraction, changing the order of numbers in a subtraction equation would absolutely change the result. Let’s understand this with an example.
Let’s subtract 3 from 4.
4 – 3 = 1
Now, if we change the order of the numbers,
3 – 4 = (-1)
Well, numbers are not bound to agree with everything all the time, right?
Division, being the most cranky of all our operators with so much to keep in mind, does not follow the law of commutativity.
Recommended Worksheets
Solved Examples on Commutative Property of Addition
Example 1: Verify that “a + b = b + a” if a = 33 and b = 30.
Solution:
Substituting the values in the left side of the equation,
a + b = 33 + 30 = 63
Substituting the values in the right side of the equation,
b + a = 30 + 33 = 63
Therefore, it is verified that a + b = b + a.
Example 2: Fill in the blanks:
20 + _ = _ + 20 = 55
Solution:
Since the result is the same, the equation must follow commutative property.
So, we can think of the missing number as “b”.
Now, we have
20 + b = 55,
Therefore b = 55 – 20 = 35.
Example 3: Prove with an example why subtraction is not applicable for commutative law?
Solution: Let us take two numbers: 3 and 5.
If we subtract 3 from 5 we get the result as 2.
But if we reverse the order and subtract 5 from 3, we get the result as –2.
Hence, the commutative property does not apply to subtraction as changing the order changes the answer.
Example 4: Which of the following fraction shows commutative property with $\frac{1}{3}$ $+$ $\frac{1}{2}$ ?
- $\frac{1}{2}$ $\times $ $\frac{1}{3}$
- $\frac{1}{3}$ $\div$ $\frac{1}{2}$
- $\frac{1}{2}$ $+$ $\frac{1}{3}$
- $\frac{1}{3}$ $-$ $\frac{1}{2}$
Solution: (c) $\frac{1}{2}$ $+$ $\frac{1}{3}$
By the law of commutativity of addition , $\frac{1}{2}$ $+$ $\frac{1}{3}$ will provide the same result as $\frac{1}{3}$ $+$ $\frac{1}{2}$.
Practice Problems on Commutative Property of Addition
Commutative Property of Addition – Definition with Examples
The following equation follows the commutative property of addition. Find the missing value.
39 + 67 = __ + 39
Using commutative property of addition,
a + b = b + a,
Therefore, 39 + 67 = 67 + 39,
Hence the missing number is 67.
Which of the following is the general form of commutative property?
The law of cummutativity states that in an addition equation, changing the order of numbers still gives the same result.
Hence, a + b = b + a.
Fill in the blanks:
23 + = + 23 = 48
Since the result is the same, the equation must follow commutative property.
So we can think of the missing number as “b”.
Now, we have
23 + b = 48,
Therefore b = 48 – 23 = 25.
If 1.22 + 3. 789 = 5.009, what is the value of 3.789 + 1.22?
By law of commutativity of addition, 1.22 + 3.789 = 3.789 + 1.22 = 5.009
Frequently Asked Questions on Commutative Property of Addition
Does the commutative property of addition apply to fractions?
Yes, as per the commutative property of addition, a + b = b + a for any numbers a and b.
Is there a commutative property for subtraction?
No, the operations of subtraction and division do not obey the laws of commutative property.
What are the properties of the addition operation?
The three properties of addition are Commutative property: For any two numbers a and b, a + b = b + a.
Associative property: For any three numbers a, b and c, a + (b + c) = (a + b) + c.
Identity property: For every number a, a + 0 = a.




































