What is Less than or Equal to?
Where equations define the equality between two or more mathematical elements; inequalities provide us with the chance of exploration when two quantities are not equal in value but are comparable in nature. An equation makes use of the “equal to (=)” symbol to express the relationship of equality between two quantities. Inequalities make use of the “greater than (>)” and “less than (<)” symbols to compare quantities that are not equal in nature.
Greater than (>):
We use “greater than” when one quantity is more than the other quantity. For example, 7 mangoes are more than 3 mangoes is mathematically expressed as 7 > 3.
Less than (<):
We use “less than” when one quantity is less than the other quantity. For example, 8 carrots are less than 10 carrots is mathematically expressed as 8 < 10.
However, in certain cases, when we only have one quantity and we want to make estimates about another quantity comparable with our first one, we use an inequality operator referred to as “Less than or Equal to ($\leq$)”.
Less than or Equal to ($\leq$)
Let’s understand this with the help of a real-life situation. David goes shopping with his mom where she lets him buy any toy for himself as long as its cost is not more than $\$10$. This means David could buy a toy worth $\$3$ or $\$4$ or $\$7$ or $\$8$ or even $\$10$ or any other cost as long as he does not exceed his limit of $\$10$. We can also say that the maximum amount he is allowed to spend is $\$10$.
Let’s say David buys a toy worth P dollars.
Then, mathematically, we can either say that P is less than 10 or that P is equal to 10 i.e.,
P < 10 or P = 10.
These two mathematical statements can be combined into one single statement as
P is less than or equal to 10.
Where we combine our “<” and “=” symbol to form “$\leq$” and we have P $\leq$ 10.
This symbol where we place a sleeping line below the less than symbol.

It provides us with a mathematical expression for the statements “at most, not more than, maximum, and not exceeding”. It can be used to compare variables or any mathematical elements or any real-life quantities.
Example:
Let’s take a look at the inequality y $\leq$ 15.
This means that the variable y is allowed to have any value less than or equal to 15. It could be 1 or 2 or 4.5 or 12/5; it could be 15 but not more than that.
Recommended Games
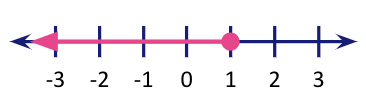
Less than or Equal to on a Number Line
Let’s look at the steps on how we can represent an inequality of the form x $\leq$ 5 on a number line.
Step 1: Locate “5” on the number line and mark it with a big circle and fill the circle.
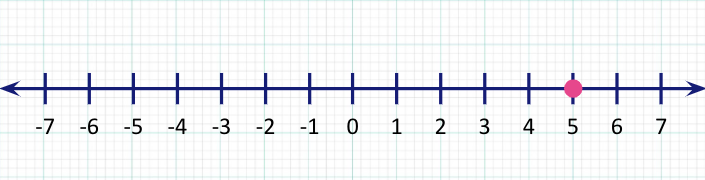
Step 2: The inequality suggests that the variable x is allowed to have any values less than or equal to 5, that means all the values on the left of this circle. Starting from here, extend an arrow to the left end signifying all the values the variable x can have.
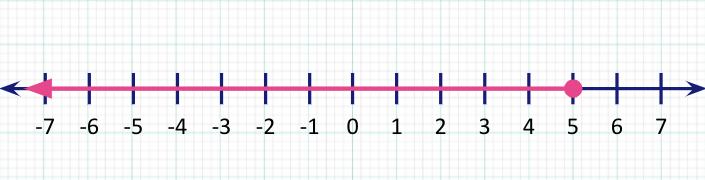
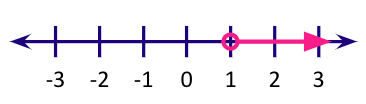
Note: If the inequality was just “less than”; we do not fill the circle as shown in the table below.
Recommended Worksheets
Difference between Comparison Symbols
| < | > |
| Less than | Greater than |
| A quantity is less than a given quantity | A quantity is greater than a given quantity |
| x<1 | x>1 |
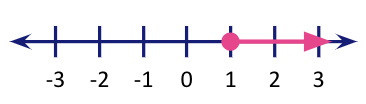
| Less than or equal to | Greater than or equal to |
| A quantity is less than or equal to a given quantity | A quantity is greater than or equal to a given quantity |
| x $\leq$ 1 | x $\ge$ 1 |
Solved Examples
Example 1: Select the numbers that are less than or equal to 55 from the given set of the numbers.
58, 0, 55, 94, 58, 5, 50, 45, 54, 59, 56, 53
Solution:
0, 55, 5, 50, 45, 54, 53
Example 2: A shop has watermelons weighing 5.3 kg, 7.6 kg, 4.5 kg, 7 kg, 6 kg and 6.1 kg. If Diana wants to buy a watermelon weighing not more than 6 kg, what are her possibilities?
Solution:
5.3 kg, 4.5 kg, 6 kg are less than or equal to 6 kg.
Example 3: A toy shop has the following items for sale.
| Doll | Scrabble | Jigsaw Puzzle | Puppet | Stuffed Toy |
| $16 | $18 | $11 | $13 | $17 |
Vivian wants to buy a toy costing less than or equal to $16. Which toys can she buy?
Solution:
Vivian can buy a doll or jigsaw puzzle or puppet as they cost less than or equal to $16.
Example 4: Graph x$\leq$ 6 on the number line.
Solution:

Practice Problems
[sp_quiz_id=”4847″]
Frequently Asked Questions
What is the difference between less than and less than or equal to?
Less than is represented by ‘<’ and less than or equal to is represented by ‘$\leq$’. Less than means that the variable or quantity has to have a value less than the given limit whereas less than or equal to means that the variable or quantity has to be equal to or less than the given limit.
What is greater than or equal to?
It is the opposite of less than or equal to and it means the given variable or quantity has to have a value equal to or greater than the given limit. For example, x $\ge$ 5 means that x can have values 5 or any number greater than that.
What are the various inequality symbols?
Greater than (>), less than (<), not equal to (≠), greater than or equal to ($\ge$), and less than or equal to ($\leq$).