In mathematics, We have whole numbers representing whole quantities,
For example, 1 pizza or 2 pizzas.
But what if we have some leftovers from a pizza that is not a whole, how do we write this mathematically?
This is where decimal numbers come to our rescue. Decimal numbers are numbers that represent quantities between whole numbers.
We get decimal numbers when we break a whole into smaller parts.
A decimal number has two components: a whole number part and a fractional part separated by a dot. Let’s see how decimal numbers are formed.
Suppose we break a whole into 10 equal parts; each part then represents $\frac{1}{10}$ of the whole or one-tenth of the whole, which is mathematically written as 0.1

Further, if we break each of these tenths into 10 equal parts, each part will represent $\frac{1}{100}$ of the whole or one-hundredth of the whole.

Note that each one-tenth is made up of 10 one-hundredths, and it is mathematically written as 0.01.
Hundredths Place Value
The hundredth place is the second place after the decimal in the decimal place value system. The decimal place value system for the whole part of a decimal number is the same as the whole number value system. However, we get the fractional part of the decimal number as we move toward the right after the ones place. A dot called the “decimal point” separates the whole and the fractional part of a decimal number.
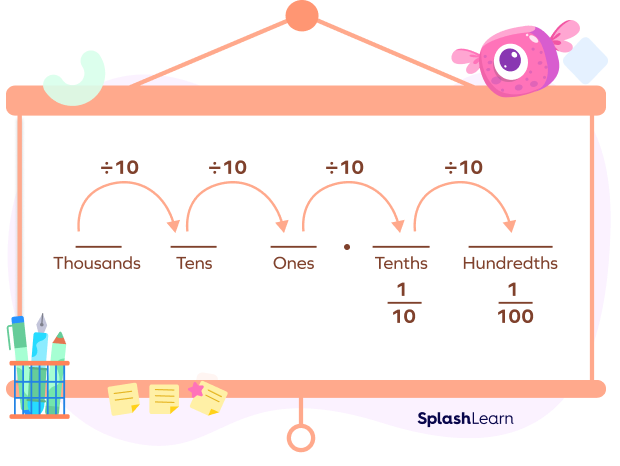
Note that as we go from left to right in the decimal place value system, each value is$\frac{1}{10}$times smaller than the value to its left.
The place value chart for decimal numbers till the hundredth place looks like this:
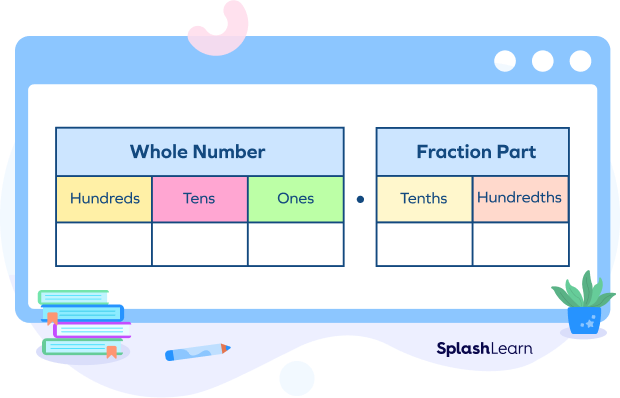
Note that the hundredth place is the second place after the decimal point.
Let’s see how we can write one-tenth as a decimal number. Remember that to write a decimal number, we need a whole part and a fractional part. Looking at this model, we have 1 column shaded to represent one-tenth. So we will write 1 in the tenths column of the place value chart; this will be the fractional part of our decimal number. Since we have nothing else, it means the whole part is 0.
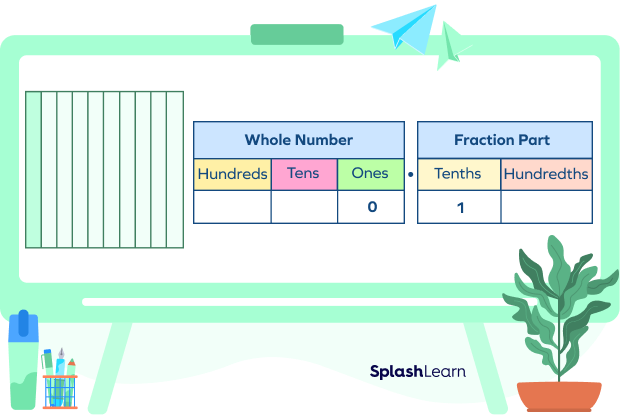
So one-tenth in decimal form is written as “0.1”.
Now, let’s see how we can write one-hundredth as a decimal number.
Using the same explanation as we did above, we have 1 hundredth, so we will write “1” in the hundredths column of the place value chart, and we have no complete tenths, so we will write 0 in the tenths column, and we have no whole. So we will write “0” in the ones column as well.
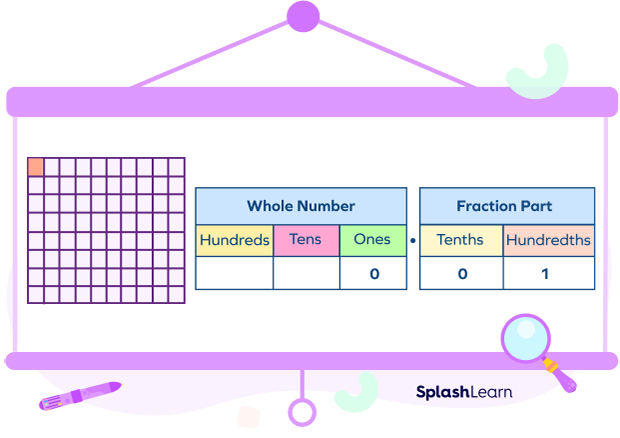
Our decimal number for one-hundredth would be “0.01”.
Now, let’s say we have 35 hundredths, it would mean that we have 35 one-hundredths, which looks like this:
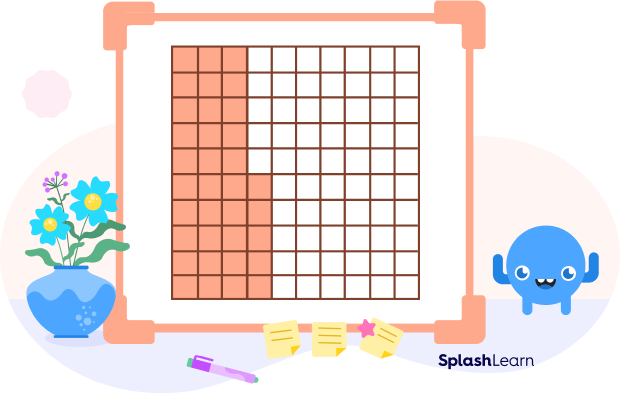
This shows that we have divided a whole into 100 equal parts, out of which we are considering only 35 parts.
so how do we write this as a decimal number?
If you notice carefully, 35 hundredths are made up of 30 hundredths and 5 hundredths., The 30 hundredths are represented by the first 3 columns of the model, and 5 more hundredths are represented as 5 blocks in the fourth column.
We know that 10 hundredths make one-tenth,
So 30 hundredths mean three 10 hundredths and that makes 3 tenths.
So, in a way, we can say that
35 hundredths = 3 tenths and 5 hundredths.
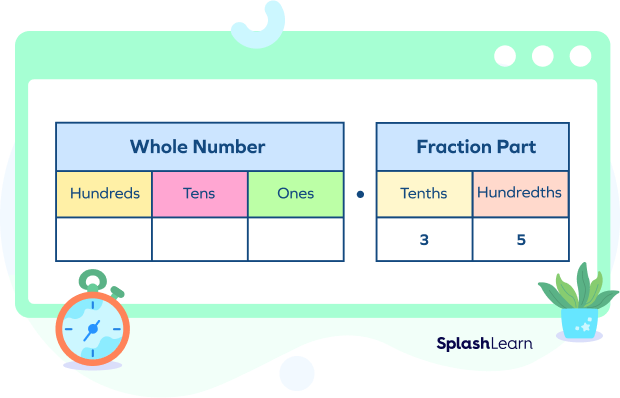
So we will use the decimal place value chart and place 3 in the tenths column and 5 in the hundredths column.
Since we don’t have any wholes here, we will write 0 in the ones place.
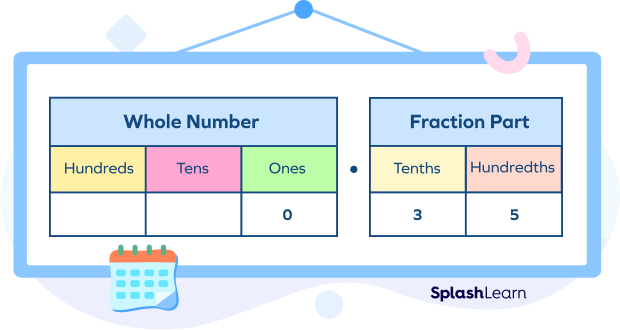
And so 35 hundredths in decimal form is written as “0.35”.
In the same way, if we had 40 hundredths, we would write it in decimal form as “0.40” we can also call this 4 tenths since 10 hundredths make 1 tenth.
Let’s consider one last example where we have two wholes and 15 hundredths, which would look like this:
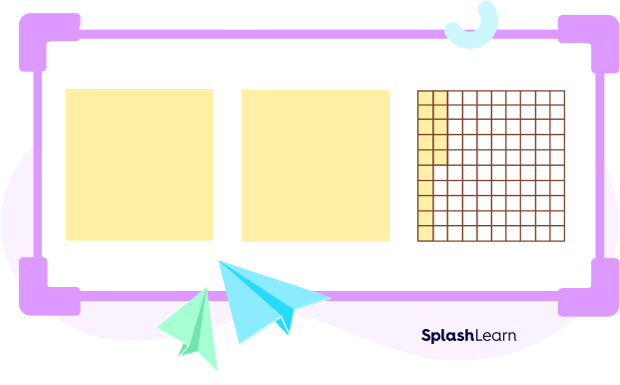
And the decimal number for this would have 2 wholes, 1 tenth, and 5 hundredths.
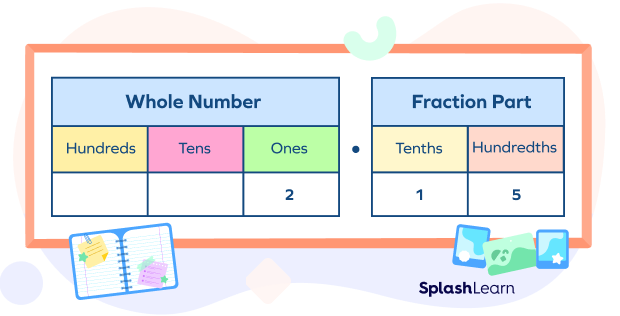
And the decimal number would be “2.15”.
Recommended Games
Difference between Hundred and Hundredth

Recommended Worksheets
Solved Examples
1. Identify the digit at the hundredth place in 234.65.
Answer: Placing this number in the decimal place value chart, we observe that,
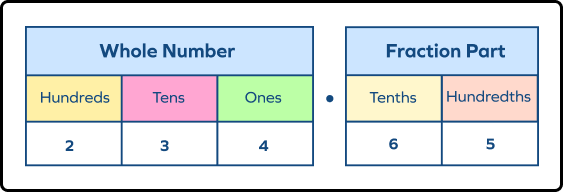
Here, the digit at the hundredths place is “5”.
2. Write $\frac{54}{100}$ as a decimal number.
Answer: $\frac{54}{100}$=0.54 or 54 hundredths.
3. Identify the place value of 6 in 54.267.Answer: The digit 6 is at the hundredth place in the given number, so its place value is $\frac{6}{100}$=0.06.
Practice Problems
One-Hundredth - Definition With Examples
Which of the following figure represents 0.57?

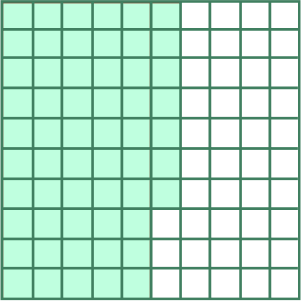
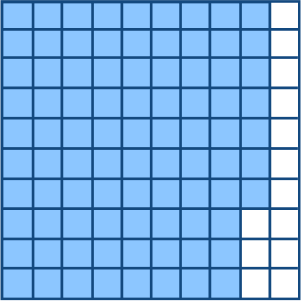
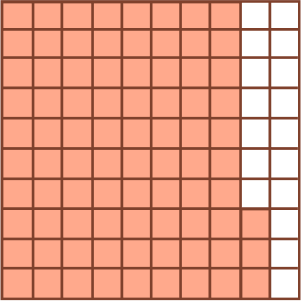
The shaded parts are 57. And the total number of parts = 100. So, it represents 0.57.
How many hundredths are there in 6 tenths?
Since one-tenth is made up of 10 hundredths, so 6 tenths = 60 hundredths.
What is the decimal form of 83 hundredths?
83 hundredths has 8 tenths and 3 hundredths so in decimal form, 83 hundredths = 0.83.
How many tenths are there in 78 hundredths?
78 hundredths is made of 70 hundredths and 8 hundredths. 70 hundredths = 7 tenths.
Frequently Asked Questions
What is the difference between tenths and hundredths?
One tenth represents one part of a whole that has been divided into 10 equal parts whereas one hundredth represents one part of a whole that has been divided into 100 equal parts.
How many tenths make a hundredth?
10 hundredths = 1 tenths. So 1 hundredths = $\frac{1}{10}$ tenths.
What are trailing zeroes?
Say, 40 hundredths can be written as 0.40, and 40 hundredths = 4 tenths = 0.4. So we can say that 40 hundredths = 0.40 = 0.4, here the last zero in the number “0.40” can be omitted and it will still represent the same value. This zero does not change the significance of the number and is called a trailing zero.




































