Power of 10 – Introduction
Ms. Kelly wrote a few equations on the board and asked her students to look for a pattern in them.
$10 × 1 = 10$
$10 × 10 = 100$
$10 × 10 × 10 = 1,000$
$10 × 10 × 10 × 10 = 10,000$
$10 × 10 × 10 × 10 × 10 × 10 = 100,000$
Let’s observe the equations together. Each equation is ten times more than the previous one. Also, the number of zeros in the product of each equation is the same as in the number of tens multiplied together.
When we multiply 10 by itself a certain number of times, we call it the power of ten. Let’s explore more about them right away!
Recommended Games
What is the Power of Ten?
An exponent of a number indicates how many times we multiply a number by itself. When we multiply 10 by itself a certain number of times, we can express that in an exponent form, also called the power of 10. Like any other exponential form, a power of 10 consists of a base and an exponent, as shown below.
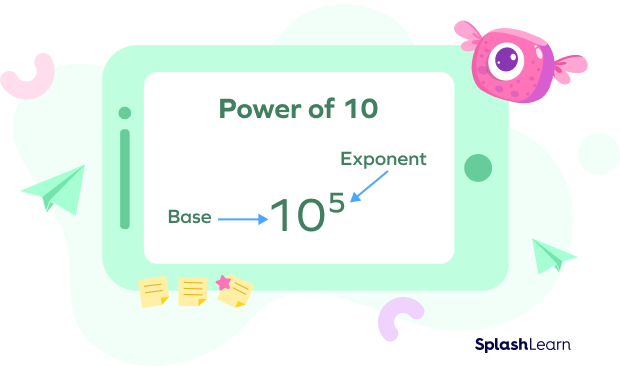
- The base of power tells us what number is being multiplied. In this case, the base is always 10.
- The exponent tells us how many times the base is multiplied by itself. The exponent can be any integer (positive, negative, or zero).
For example, 10n has base 10 and exponent n, where n is an integer. 10n is read as “10 to the power of n.”
Recommended Worksheets
Expanded Form
Power of any number is an expression that represents repeated multiplication of the number. It is represented as xn. The exponent of the power tells us how many times the number is multiplied to itself.
For example, when the exponent is 3, we multiply 10 by itself 3 times.
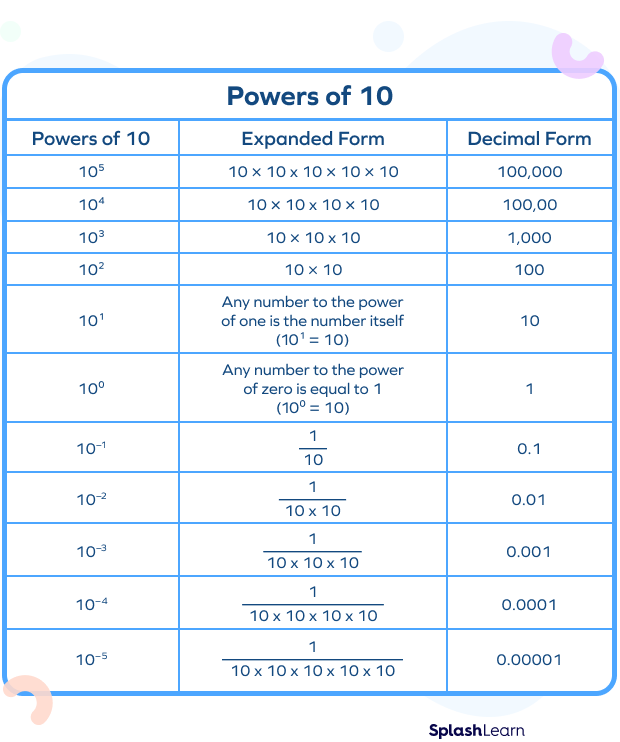
103 = 10 × 10 × 10, this is also called the expanded form of the power.
Positive and Negative Exponents
The exponent of a power of ten can be a positive or negative integer. When the exponent is positive, we can write the power in the expanded form and find the product.
For example, 104 = 10 × 10 × 10 × 10 = 10,000. The number of zeros in the product is equal to the exponent.
When the exponent is negative, we can apply the rules of exponent, x-a = 1/xa, and find the value.
For example, 10-4 = 1/104 = 1/10000 = 0.0001
In general, we can write the value in decimals by observing the exponent. The value is a decimal point followed by as many zeros as one less than the exponent and a 1. When the exponent is negative, the value is always less than 1.
Any number raised to the power 0 is one, and ten is no exception. When the exponent is 0, the value is 1.
What Is the Use of Powers of Ten?
Scientists and engineers often encounter very big or small numbers. For example, if scientists have to send a spacecraft to the moon, it should travel at least 240,000 miles, which is the distance between Earth and the Moon. Such numbers can be troublesome to use in their original form. So, scientists use a notation where they write the number in terms of the power of 10. For example, a large number like 50,000,000 can be represented as 5 × 107.
A complicated number like 456,000 can be written as 456 × 103 or 4.56 × 105, which is a scientific notation.
A scientific notation of a positive number is to express the number as the product of a number less than 10 and a power of 10. In case the number is greater than 1, then the exponent (in the scientific notation) is a positive number. If the number is less than 1, then the exponent will be a negative number. For example, a small number like 0.00005 can be written as 5 × 10-5.
Solved Examples
Example 1: Write 10,000,000 as a power of 10.
Solution: There are 7 zeros in 10,000,000. So, we can write the given number as 7th power of ten or 107.
Example 2: Find the product of 5.65 × 10⁴.
Solution: When multiplying the number by the power of 10, we move the decimal points to the right side.
So, 5.65 × 10000 = 56,500
Example 3: George and Melissa are contending for the position of mayor. The total number of votes cast for each candidate is:
George: 7 × 10⁴
Melissa: 105
Who won the election?
Solution: George received 7 × 10⁴ or 70,000 votes
Melissa got 105 or 100,000 votes.
Clearly, Melissa won the election.
Practice Problem
Power of 10 - Definition with Example
Find the value of n that would make the equation true.
$10^{n} = 100,000$
Since 100,000 has 5 zeros, we can write this as the 5th power of ten or $10^{5}$.
Which of the following numbers is equivalent to $10^{4}$?
$10^{4} = 10 × 10 × 10 × 10 = 10,000$
Which of the following is greater than 10?
$10^{0} = 1$. When the power of 10 is negative, the value is less than 1.
Frequently Asked Questions
What is the difference between 102 and 210?
In 102, the base is 10, and the exponent is 2. That is, ten is being multiplied to itself twice.
102 = 10 × 10 = 100.
In 210, the base is 2, and the exponent is 10. That is, 2 is being multiplied to itself ten times.
210 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
Is 104 equal to 10-4?
No, different powers of 10 have different values.
104 = 10000 and 10-4 = 1/10000
So, they both are different, and 104 > 10-4
Also, since the exponent of 104 is 4 > 1, the value of the power is greater than 10.Since the exponent of 10-4 is negative, the value of the power is less than 1.
How can we write the expanded form 18964 as the power of ten?
The expanded form of 18964
= 10000 + 8000 + 900 + 60 + 4
= 104 + 8 × 103 + 9 × 103 + 6 × 10 + 4




































