What Is an Obtuse Angle?
An obtuse angle is an angle with angle measure greater than 90° and less than 180°. In other words, it lies between 90° and 180°.
So, what does an obtuse angle look like? How many degrees does an obtuse angle measure? Take a look at the given Obtuse Angle diagram to understand its range better.
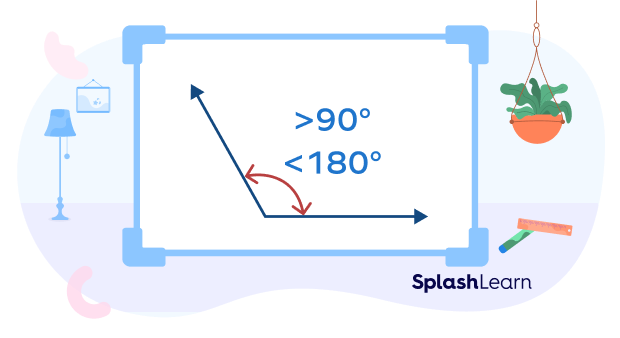
An angle is a geometric figure formed when two rays meet at a common point called vertex.
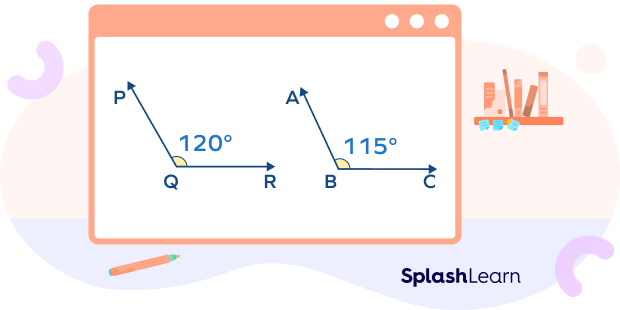
Examples of obtuse angles: In the given figure, the angles ∠XYZ and ∠ABC are obtuse angles.
Recommended Games
Obtuse Angle: Definition
An angle that measures greater than 90° but less than 180° is called an obtuse angle.
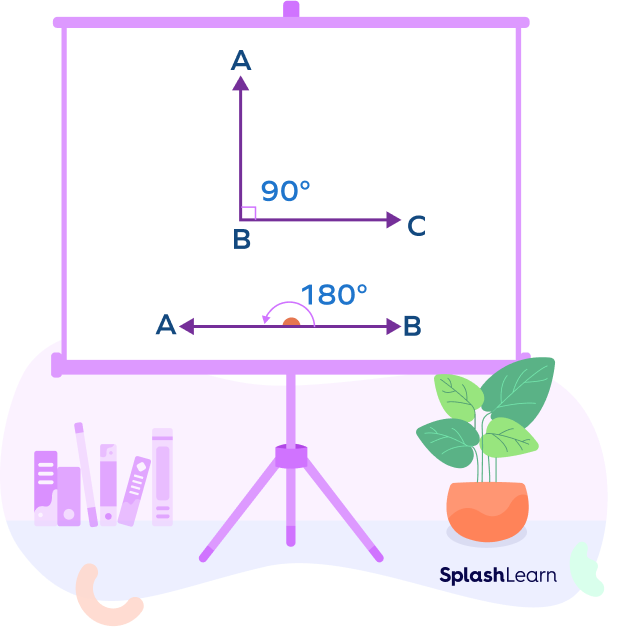
So, what about angles that measure 90° or 180°? Are they obtuse angles? No!
- An angle that measures 90° is a right angle.
- An angle that measures 180° is a straight angle.
Basically, if an angle is greater than a right angle but smaller than a straight angle, we can call it an obtuse angle.
Recommended Worksheets
Degree Range for Obtuse Angles
An obtuse angle measures more than 90 degrees (a right angle) but less than 180 degrees (a straight angle). Thus, the obtuse angle degree range is (90°,180°).
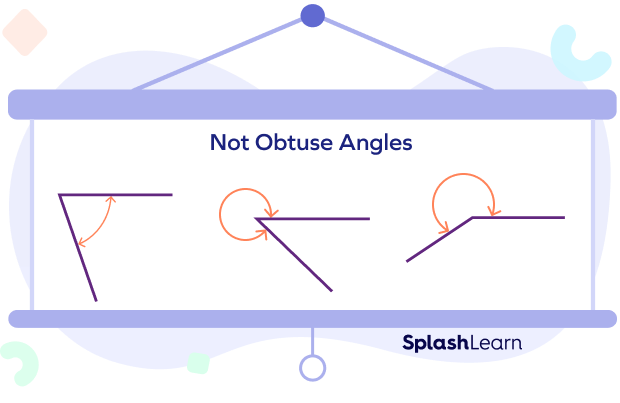
Take a look at a few examples of obtuse angles.
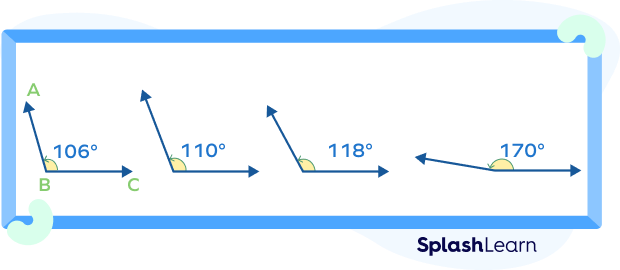
Also, take a look at the non-examples of an obtuse angle.
How to Construct an Obtuse Angle
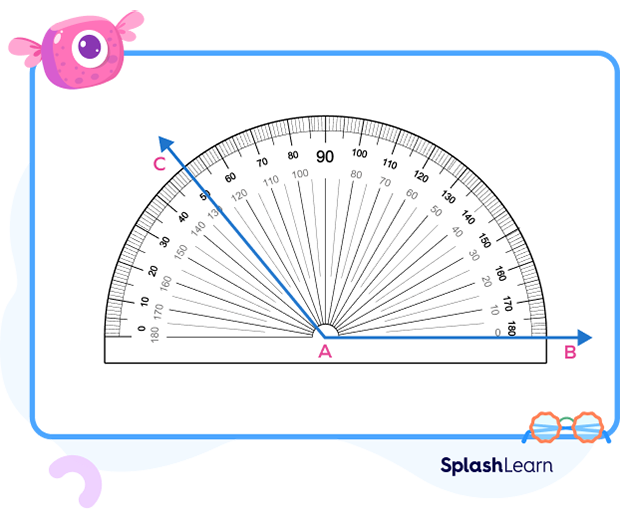
Let us learn the steps to draw an obtuse angle using a protractor. Let’s draw an obtuse angle that measures 130°.
Step 1: First, draw a straight line AB. It will serve as a base line.
Step 2: Place the center of the protractor at point A.
Step 3: Choose the inner scale which has 0 degrees marking near point B for construction. Mark a dot at 130° and name it C.
Step 4: Join A and C.
Properties of Obtuse Angles
- An obtuse angle measures between 90º and 180º.
- An obtuse angle is greater than a right angle and an acute angle, but it is smaller than a straight angle (180º).
- The size of an obtuse angle appears bigger than a quarter of a circle but less than a semicircle.
- An obtuse angle is always greater than an acute angle.
- An obtuse angle is always less than a reflex angle, straight angle, and a complete angle.
Obtuse Triangle (Obtuse Angled Triangle)
An obtuse triangle is a triangle in which one of the interior angles measures more than 90°. The remaining two angles are acute angles.
The side opposite to the obtuse angle is the longest side of the obtuse triangle.
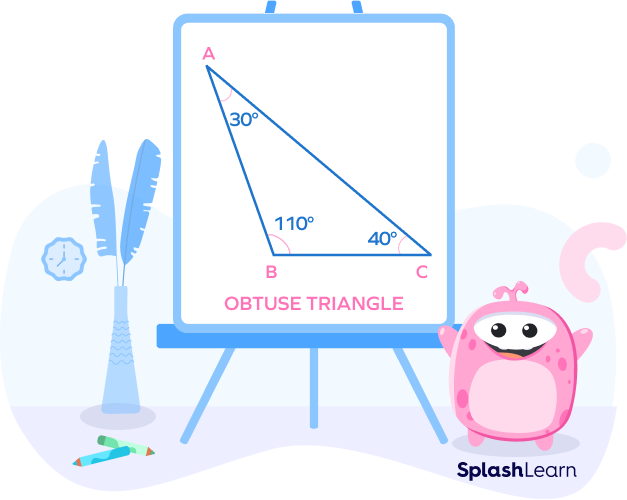
There are two types of obtuse triangles: Isosceles and Scalene. An obtuse equilateral triangle does not exist.
Types of Angles
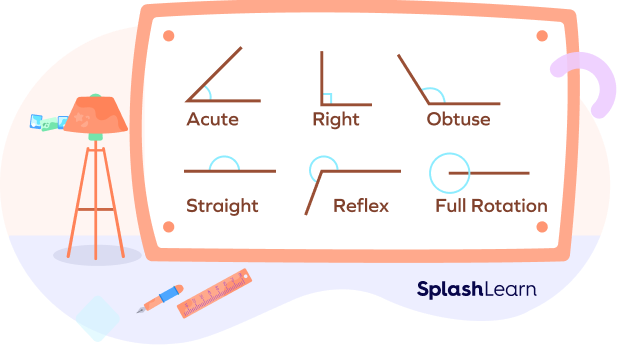
Let’s take a quick look at the different types of angles based on their measurements.
- Zero angle: An angle that measures 0°.
- Acute angle: An angle that measures less than 90° (between 0° and 90°).
- Right angle: An angle that measures 90°.
- Obtuse angle: An angle that measures greater than 90° and less than 180°
- Straight angle: An angle that measures 180°.
- Reflex Angle: An angle that measures greater than 180° and less than 360°.
- Complete Angle: An angle that measures 360°.
Obtuse Angles in Polygons
Let’s see a few examples of an obtuse angle in different polygons.
- Obtuse Angle in a Triangle (BOLD)
In triangle MNO, ∠N = 96° is an obtuse angle.
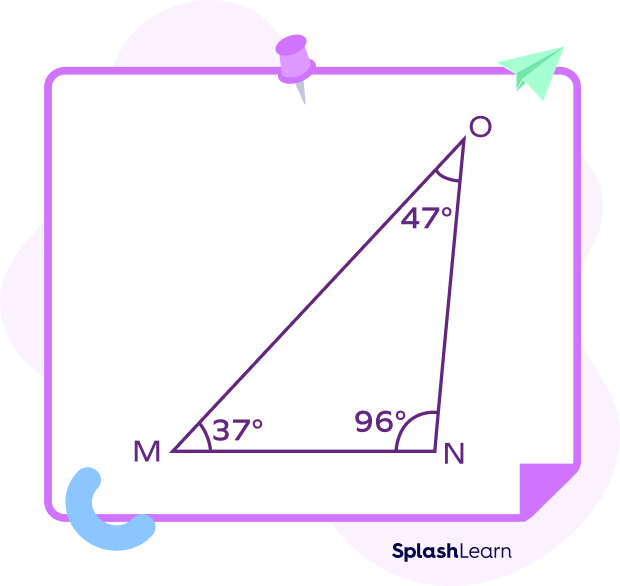
- Obtuse Angle in a Parallelogram (BOLD)
In parallelogram PQRS, ∠P = 135° is an obtuse angle.
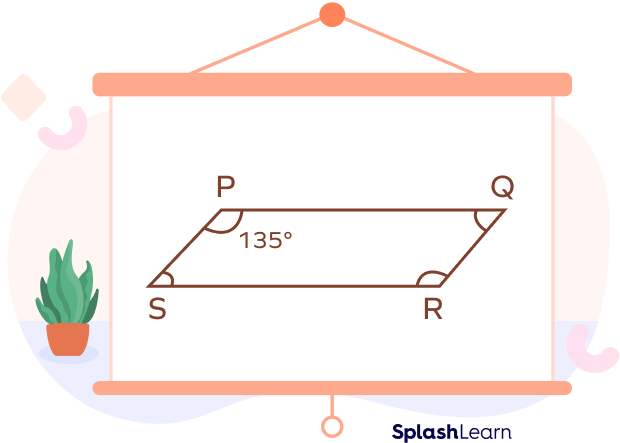
- Obtuse Angle in a Regular Hexagon (BOLD)
In the regular hexagon ABCDEF, all the angles are obtuse.
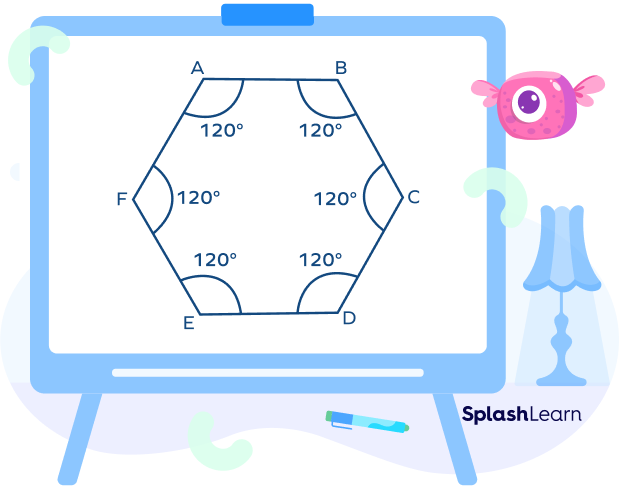
Real-life Examples of Obtuse Angles
Let’s take a look at some examples of obtuse angles in real life.
Look at the girl in the picture below. Notice that the outline of her hands forms an angle that is higher than 90° but lower than 180°. Similarly, you can try to find obtuse angles in different objects around you!

Solved Examples on Obtuse Angles
1. Identify the types of interior angles in the given triangle. Is there an obtuse angle present?
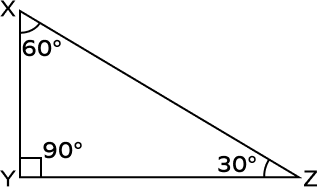
Solution:
The triangle has 3 angles.
The angle Y is a 90° angle. It’s the right angle.
The angles X and Z measure 60° and 30° respectively. They are acute angles.
There are no obtuse angles in this triangle.
2. What is the difference between an obtuse angle and an acute angle? Explain with an example.
Solution:
| Obtuse angle | Acute angle |
|---|---|
| An angle that is larger than 90° but smaller than 180° is called an obtuse angle. | An angle that is smaller than 90° but larger than 0° is called an acute angle. |
| A triangle is called an obtuse triangle if it has one obtuse angle and two acute angles. | A triangle is called an acute triangle if it has three acute angles. |
For example, look at the hands of this clock. The angle is greater than 90° but less than 180°. So, we can call it an obtuse angle.  | For example, look at the hands of this clock. The angle of the minute hand and hour hand is smaller than 90°. So, it is an acute angle.  |
3. Identify the types of angles in the triangle ABC.
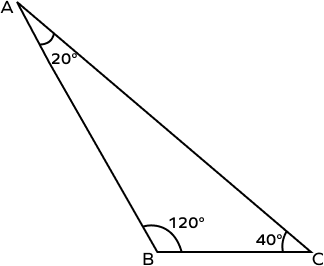
Solution:
The triangle ABC has 3 angles.
∠A = 20° and ∠C = 40° are acute angles.
∠B = 120° is an obtuse angle as it is greater than 90° but less than 180°.
Thus, the triangle ABC is an obtuse triangle.
4. In the given hexagon ABCDEF, can you tell which angles are obtuse and which are not?
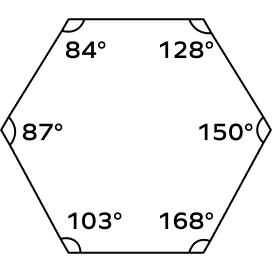
Solution:
In the given hexagon ABCDEF, there are 6 angles.
∠A = 84° …Acute angle
∠B = 128° …Obtuse angle
∠C = 150° …Obtuse angle
∠D = 168° …Obtuse angle
∠E = 103° …Obtuse angle
∠F = 87° …Acute angle
Practice Problems on Obtuse Angles
Obtuse Angle - Definition, Degree, Properties, Examples, FAQs
Which of these angles is an obtuse angle?
As the angle 179° is larger than 90° but smaller than 180°, it is an obtuse angle.
Which among these is not an obtuse angle?
As this angle is smaller than 90°, it is not an obtuse angle but an acute angle.
Find the odd one out.
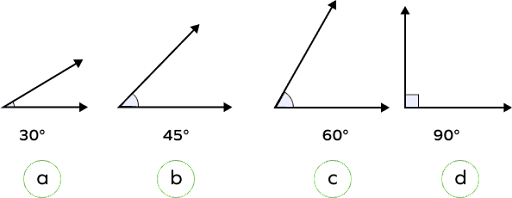
Angles in the first three options are acute angles. Angle that measures exactly 90° is a right angle.
What is the range of an obtuse angle?
The range of an obtuse angle is (90°,180°).
Frequently Asked Questions about Obtuse Angles
Is 180 degrees an obtuse angle?
No. An angle that measures 180 degrees is a straight angle.
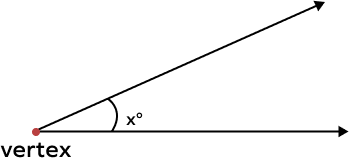
What is the point at which two rays meet to form an angle known as?
The point where two rays meet to form an angle is known as the vertex.
What do we call an angle which is exactly 90°?
An angle that is exactly 90° is known as a right angle. A right angle is larger than an acute angle but smaller than an obtuse angle.
What is a 360 degree angle called?
A 360 degree angle is called a full angle or a complete angle.





























