What is an Angle Measure?
An angle is formed when two lines or rays meet at a common point. The common point is known as the vertex.
In geometry, an angle measure can be defined as the measure of the angle formed by the two rays or arms at a common vertex.
For example, in the illustration below, the yellow region measures the span of the angle.
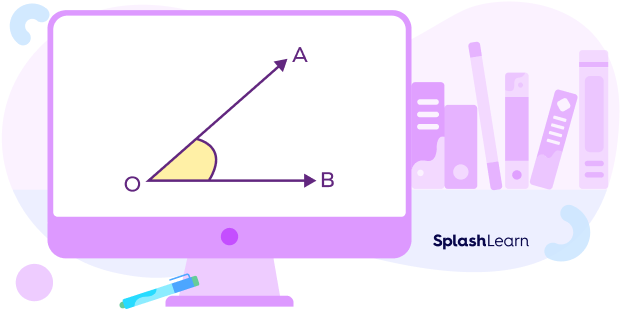
Recommended Games
How to Find the Measure of an Angle?
Angles are measured in degrees (°) using a protractor. A protractor is a measuring device that is used to calculate or draw angles in terms of degrees.
For example, in the image below, we see that using a protractor, the black arrow points to 100°, crossing 90°. Hence, the measure of the angle is 100°.
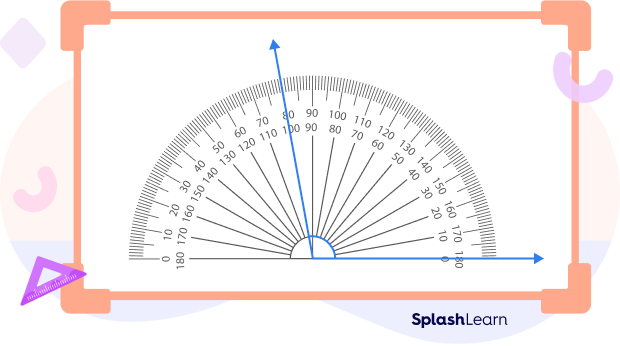
To determine the angle measure with a protractor, follow the steps below:
- Position the middle point or midpoint of the protractor on the vertex of the angle.
- Place one side of the angle on the zero-marked line of the protractor (at the point you observe the numeral 0).
- Find the degree measure at which the other side of the protractor points the angle.
Recommended Worksheets
Types of Angles
There are many kinds of angles in geometry: acute, obtuse, reflex, straight, and right angle. Each angle has a different measure.
There are also special types of angle pairs. Let’s first take a look at the various types of angles.
Types of Angles Based on Measurement
Right Angle
An angle between two rays measuring exactly 90° is called a right angle.
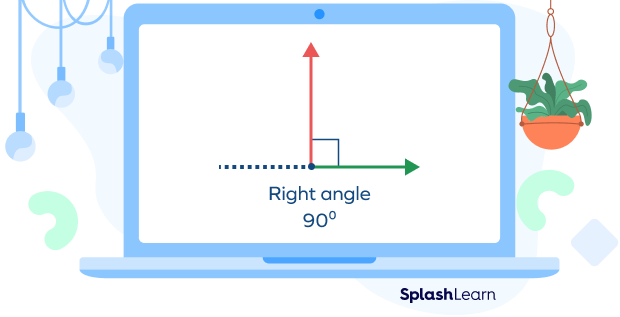
Acute Angle
An acute angle is formed when two rays intersect at the vertex and form an angle smaller than 90°. Some examples of acute angles are 20°, 40°, 60°, and 80°.

Obtuse Angle
Obtuse angles are any angles that measure greater than 90° and smaller than 180°. Some examples of obtuse angles include 110°, 130°, 145°, and 165°.
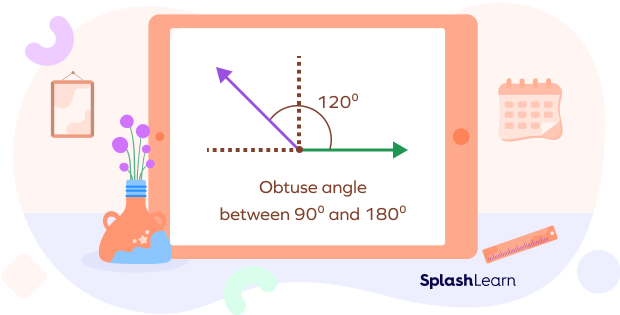
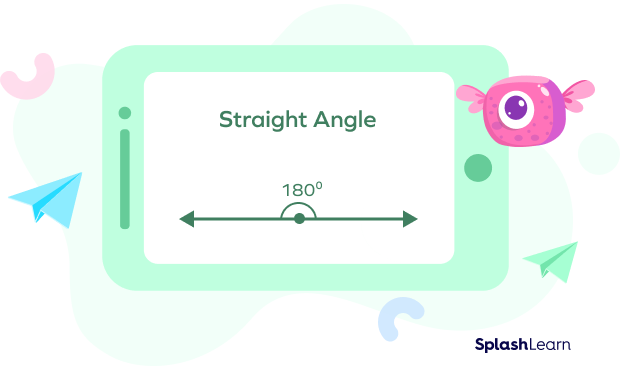
Straight Angle
Straight angles are, as the name implies, straight lines. The two rays that form a straight angle are opposite each other. The angle between the two rays is 180°. Two adjacent right angles can be combined to create a straight angle.
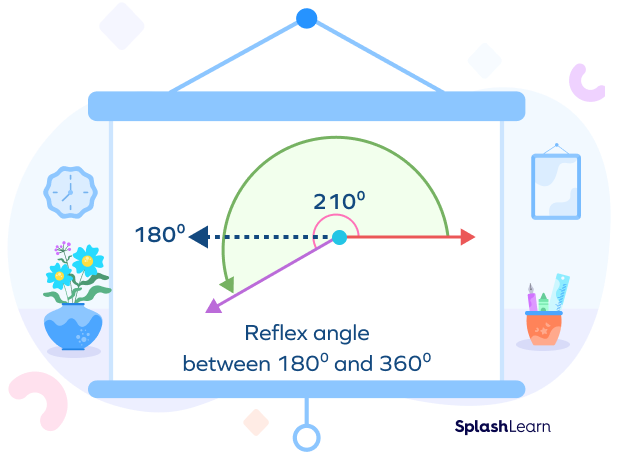
Reflex Angle
A reflex angle is an angle greater than 180° or less than 360°. Some examples of reflex angles include
210° and 250°.
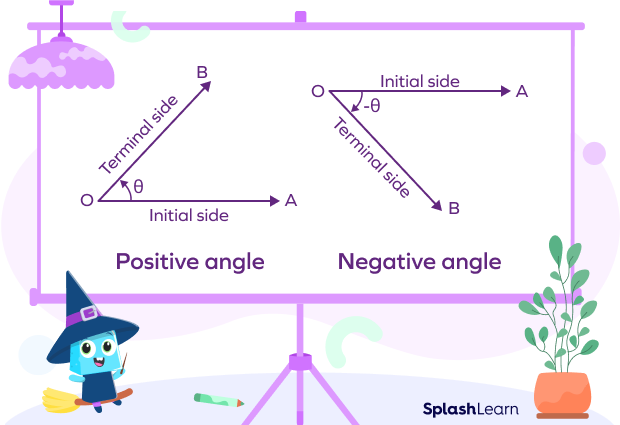
Types of Angles Based on Rotation
Positive Angles
An angle with the degree of the ray’s rotation from its starting point to its final position in a counterclockwise direction is referred to as a positive angle. The direction counterclockwise is considered to be a positive direction within the sense of angle.
Negative Angles
Negative angles are angles that are rotated in the clockwise direction from the base.
Types of Angle Pairs
A pair of angles is a combination of two angles. Let’s learn more about the different angle pairs in geometry.
Adjacent Angles

The following conditions must be met for two angles to be considered adjacent:
- The two angles share the same vertex.
- The two angles share one arm.
Complementary Angles
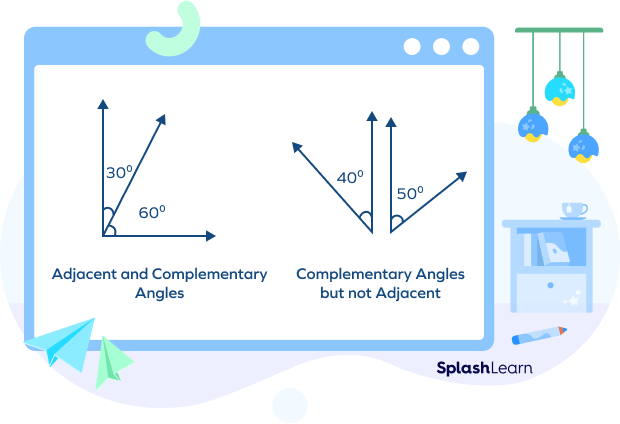
Complementary angles are angles whose sum equals 90°. Complementary angles can be adjacent or non-adjacent.
For example, the given image shows adjacent and non-adjacent complementary angles.
In the first image, the sum of angle measures is $30°+ 60°=90°$
In the second image, the sum of angle measures is $50°+ 40°=90°$
Supplementary Angles
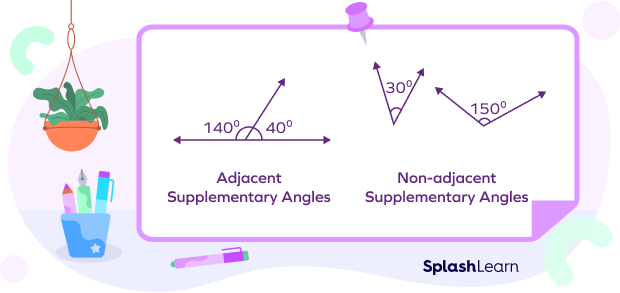
Supplementary angles are angles which add up to 180° i.e. the sum of their angle measures is 180°.
If the two supplementary angles are adjacent to each other, they are called ‘angles in linear pair’.
For example, in the above image, the angles measuring 140° and 40° are supplementary and adjacent. So, they form a linear pair.
On the other hand, the angles measuring 150° and 30° are supplementary but not adjacent.
Corresponding Angles
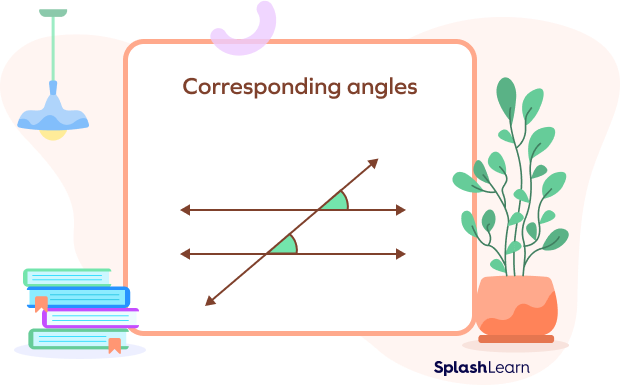
Consider two parallel lines. When these are intersected by another line, i.e, a transversal, the angles created in the corresponding corners are known as corresponding angles.
Vertical Angles
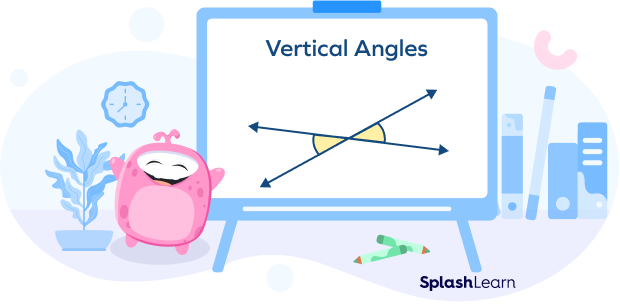
When two lines intersect, the angles opposite each other are equal. These are called vertical angles or vertically opposite angles.
Let’s sing!
Acute angles are a tiny bit smaller than normal.
The corner of a wall is at a right angle
The obtuse angle at 2.50 in the daytime
Straight bend in a straw made of soda-lime
There are so many angles, even in mimes!
Solved Examples
1. If ∠A is 55°, then what type of angle is it?
Solution: $∠A = 55°$
An acute angle is formed when two rays intersect at the vertex and form an angle that is smaller than 90°. Since a 55° angle is smaller than 90°, it is an acute angle.
2. What is an angle pair measuring 55° and 35° called?
Solution: Complementary angles are angles whose sum equals 90°.
Since the sum of these angles equals $90° (55° + 35° = 90°)$, we call them complementary angles.
3. If ∠P is 210°, then what type of angle is it?
Solution: A reflex angle is an angle greater than 180° or less than 360°. Since ∠P measures 210°, it is a reflex angle.
Practice Problems
Angle Measure
What is a 90° angle called?
In geometry and trigonometry, a right angle is an angle of precisely 90°.
What are angles measuring 80° and 10° called?
Two angles are called complementary if their measures add to 90°.
What is a 45° angle called?
An angle measuring less than 90° is called an acute angle.
What are angles measuring 120° and 60° called?
Two angles are called supplementary when their measures add up to 180°.
Frequently Asked Questions
What are the two conditions to be met for an angle to be called an adjacent angle?
The following conditions must be met for two angles to be considered adjacent:
- The two angles share the same vertex.
- The two angles share one arm.
What kinds of angles can be measured using a protractor?
A protractor can be used to measure the following kinds of angles: acute angles, straight angles, obtuse angles, right angles, full rotation angles, and reflex angles.
Which sign is used to represent an angle?
The sign ∠ is used to represent an angle.




































