What Are Interior Angles?
The term “interior angles” in geometry can be used in two different contexts.
- Interior angle formed when two parallel lines are cut by a transversal
- Interior angles formed inside a polygon (a shape)
Let’s explore the meaning of interior angles with respect to each of these cases along with types, different formulas and examples.
Interior Angles Definition
The angles that lie inside a polygon are called interior angles of a polygon. When two parallel lines are cut by a transversal, the angles that lie between the two parallel lines are known as interior angles.
Interior Angles Formed When Two Parallel Lines Are Cut By a Transversal
The angles that lie in the area enclosed between two parallel lines cut by a transversal are also called interior angles.
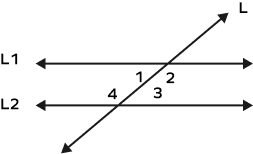
Observe the image shown below.
Here, the lines L1 and L2 are parallel lines.
L is the transversal that intersects these lines.
$\angle 1,\; \angle 4,\; \angle 2,\; \angle 3$ are interior angles.
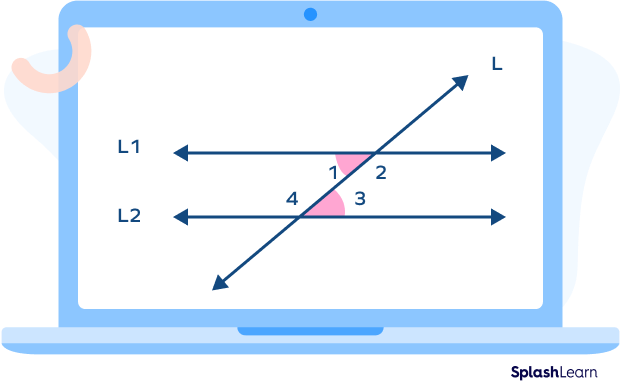
We will refer to this image to understand the types of the interior angles.
Recommended Games
What Are the Types of Interior Angles?
Two types of interior angles are formed when a transversal cuts two parallel lines:
- Co-interior angles or Same Side Interior Angles
- Alternate interior angles
Same Side Interior Angles (Co-interior Angles)
These are pairs of non-adjacent angles that lie on the same side of the transversal. The sum of two co-interior angles is $180^\circ$. They are supplementary.
The angle pairs that form same-side interior angles in the above image are
- $\angle 1$ and $\angle 4$ such that $\angle 1 + \angle 4 = 180^\circ$
- $\angle 2$ and $\angle 3$ such that $\angle 2 + \angle 3 = 180^\circ$
Alternate Interior Angles
Alternate interior angles lie on the opposite sides of the transversal. The Alternate Interior Angles Theorem states that if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.
The angle pairs that form alternate interior angles in the above image are:
- $\angle 1$ and $\angle 3$ such that $\angle 1 =\angle 3$
- $\angle 2$ and $\angle 4$ such that $\angle 2 =\angle 4$
Recommended Worksheets
Interior Angles of a Polygon
The angles that lie inside a polygon formed by the sides are called interior angles.
The following image shows interior angles of a triangle and a pentagon.
Note that the number of interior angles in a polygon is always equal to the number of sides.
Interior angles examples:
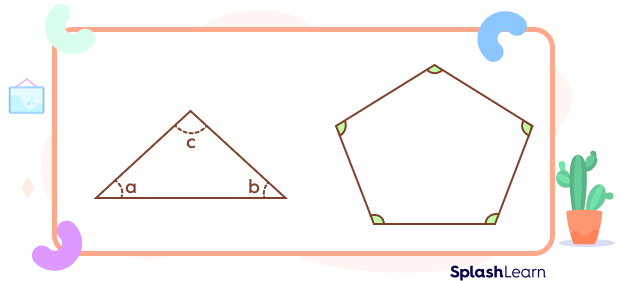
Interior Angles of a Triangle
A triangle has three interior angles. The sum of three interior angles of a triangle always sums up to 180°. If we bisect these angles, the angle bisectors meet at a point called the incenter.
Since the sum of interior angles of a triangle is 180°, only one right angle or only one obtuse angle is possible in each triangle.
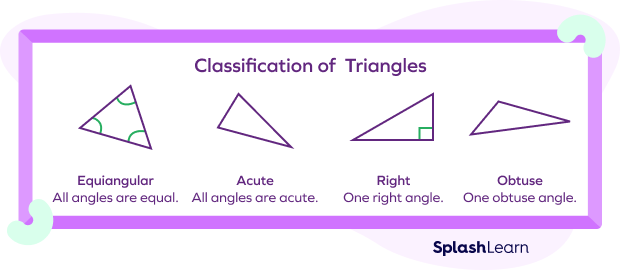
Classification of Triangles Based on Interior Angles
- Acute Triangle: A triangle which has all three interior angles as acute is called an acute triangle.
- Obtuse Triangle: A triangle whose one interior angle is an obtuse angle and other two angles are acute is known as an obtuse triangle.
- Right Triangle: A triangle which has one interior angle is a right angle and other two angles are acute is known as a right-angled triangle.
A triangle in which all the angles are of equal measure is called an equiangular triangle. It basically is the equilateral triangle in which all interior angles are 60 degrees.
Sum of Interior Angles Formula
If we take the simplest polygon, a triangle, or any polygon with n sides, all the sides of a polygon will create interior and exterior angles.
As per the angle sum theorem, the sum of all the three interior angles of a triangle is equal to $180^\circ$. Let us now see the formula to calculate the sum of interior angles of any polygon with “n” sides.
Sum of interior angles formula:
Sum of interior angles of a polygon $= S = (n \;−\; 2) \times 180^\circ$
Here, $S =$ Sum of interior angles
$n =$ number of sides of the polygon.
Let us apply this formula on a triangle and check the result:
$S = (n\;−\;2) \times 180^\circ$
$S = (3\;−\;2) \times 180^\circ$
$S = 1 \times 180^\circ$
$S = 180^\circ$
Let us look at a table to understand how to use the same formula to calculate the sum of the interior angles of polygons:
| Polygon | Number of Sides (n) | Sum of Interior Angles |
| Triangle | 3 | $180^\circ\times(3\;-\;2) = 180^\circ$ |
| Quadrilateral | 4 | $180^\circ\times(4\;-\;2) = 360^\circ$ |
| Pentagon | 5 | $180^\circ\times(5\;-\;2) = 540^\circ$ |
| Hexagon | 6 | $180^\circ\times(6\;-\;2) = 720^\circ$ |
| Heptagon | 7 | $180^\circ\times(7\;-\;2) = 900^\circ$ |
| Octagon | 8 | $180^\circ\times(8\;-\;2) = 1080^\circ$ |
| Nonagon | 9 | $180^\circ\times⨯(9\;-\;2) = 1260^\circ$ |
| Decagon | 10 | $180^\circ\times(10\;-\;2)= 1440^\circ$ |
Finding an Unknown Interior Angle
We use the “Sum of Interior Angles Formula” to find an unknown interior angle of a polygon.
Let us consider an example to find the missing angle $\angle x$ in the following quadrilateral.
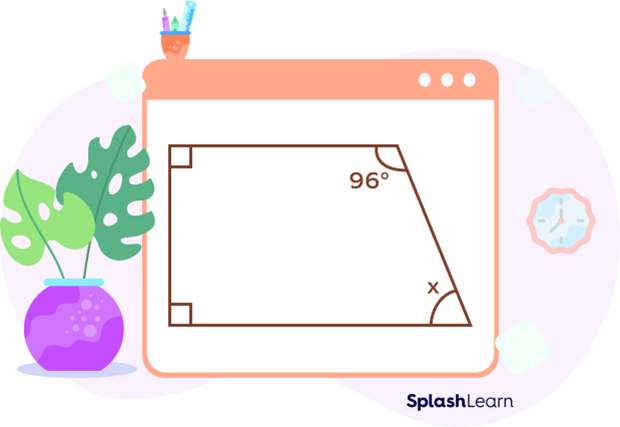
From the above given interior angles of a polygon table, the sum of the interior angles of a quadrilateral is $360^\circ$. Two of the interior angles of the above quadrilateral are right angles.
Thus, we get the equation:
$90 + 90 + 96 + x = 360^\circ$
Let us solve this to find x.
$276 + x = 360$
$x = 360\;-\;276 = 84^\circ$
Therefore, the missing interior angle x is $84^\circ$.
Interior Angles of Regular Polygons
When all the sides and angles of a polygon are congruent, it is known as a regular polygon. Let us look at some examples of regular polygons:
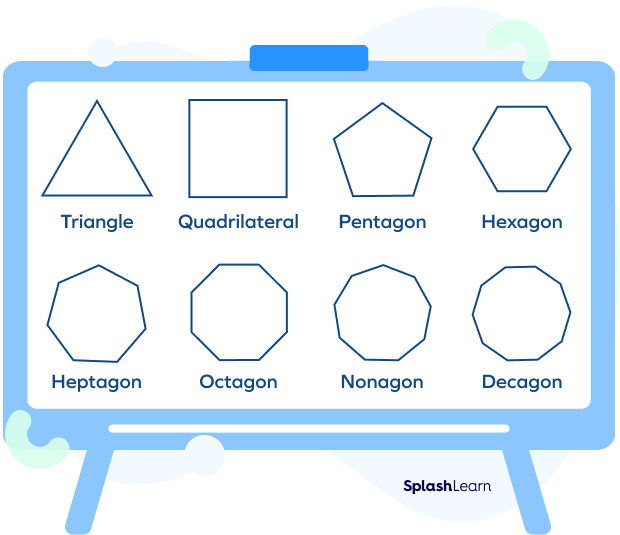
We already studied that the formula to calculate the sum of the interior angles of any polygon of “n” sides is $180^\circ(n\;-\;2)$. As we know that there are “n” angles in a regular polygon which have “n” sides.
Since all the interior angles of a regular polygon are equal, each interior angle can be calculated by dividing the sum of the angles by the number of sides.
Each interior angle of a regular polygon $= \frac{180^\circ \times (n\;-\;2)}{n}$
Let us use this formula to calculate the interior angle of a regular hexagon. We know that the number of sides of a hexagon is 6 (Here, $n = 6$).
Each interior angle of a regular hexagon $= \frac{180^\circ\times(n\;-\;2)}{n}$
$= \frac{180^\circ\times(6\;-\;2)}{6}$
$= \frac{180\times4}{6}$
$= \frac{720^\circ}{6}$
$=120^\circ$
Therefore, each interior angle of a regular hexagon is equal to $120^\circ$.
| Regular Polygon | Sides(n) | Sum of Interior Angles (S) | Measure of Each Interior Angle |
| n-sided polygon | n | $180^\circ\times(n\;-\;2)$ | $\frac{180^\circ(n\;-\;2)}{n}$ |
| Triangle | 3 | $180^\circ(3\;-\;2) = 180^\circ$ | $\frac{180^\circ}{3} = 60^\circ$ |
| Square | 4 | $180^\circ(4\;-\;2) = 360^\circ$ | $\frac{360^\circ}{4} = 90^\circ$ |
| Pentagon | 5 | $180^\circ(5\;-\;2) = 540^\circ$ | $\frac{540^\circ}{5} = 108^\circ$ |
| Hexagon | 6 | $180^\circ(6\;-\;2) = 720^\circ$ | $\frac{720^\circ}{6} = 120^\circ$ |
| Heptagon | 7 | $180^\circ(7\;-\;2) = 900^\circ$ | $\frac{900^\circ}{7} = 128.57…^\circ$ |
| Octagon | 8 | $180^\circ(8\;-\;2) = 1080^\circ$ | $\frac{1080^\circ}{8} = 135^\circ$ |
| Nonagon | 9 | $180^\circ(9\;-\;2) = 1260^\circ$ | $\frac{1260^\circ}{9} = 140^\circ$ |
| Decagon | 10 | $180^\circ(10\;-\;2) = 1440^\circ$ | $\frac{1440^\circ}{10} = 144^\circ$ |
Facts about Interior Angles
- If we intersect two straight lines, the opposite angles (vertically opposite angles) are equal. These angles have a common vertex and a common side.
- If any side of a triangle is extended, the exterior angle thus formed is equal to the sum of two remote interior angles. This is known as the Exterior Angle Theorem.
Conclusion
In this article, we learned about interior angles, their types along with formulas. Now let us solve some examples and practice problems to understand the above concepts.
Solved Examples on Interior Angles
1. Five interior angles of an irregular hexagon are: $100^\circ,\; 130^\circ,\; 95^\circ,\; 125^\circ$ and $110^\circ$. What is the value of its sixth angle?
Solution:
We know that the sum of angles of a hexagon is $720^\circ$.
Let the unknown angle be x.
$100^\circ + 130^\circ + 95^\circ + 125^\circ + 110^\circ + x =720^\circ$
$560^\circ + x = 720^\circ$
$x = 720^\circ\;-\;560^\circ$
$x = 160^\circ$.
Therefore, the value of the unknown angle is $160^\circ$.
2. What is the sum of interior angles of a polygon with 15 sides?
Solution:
The formula to calculate the sum of interior angles of any polygon with “n” sides is Sum=(n−2) × 180°
Given, $n = 15$.
$Sum = (15 \;-\; 2) \times 180^\circ$
$= 13 \times 180^\circ$
$= 2340^\circ$
Therefore, the sum of interior angles of a polygon with 15 sides is $2340^\circ$.
3. What will be the measure of each angle for a regular 15-gon?
Solution:
If the 15 sided polygon is regular, then the measure of each angle will be the total sum of all angles divided by the number of sides.
So, measure of each angle $= \frac{(n\;−\;2)\times180^\circ}{n} = \frac{2340}{15}=156^\circ$.
Hence, the measure of each angle in a 15 sided regular polygon is $156^\circ$.
4. In the figure given below, if m$\angle 1 = 105^\circ$, what is the value m$\angle 3$?
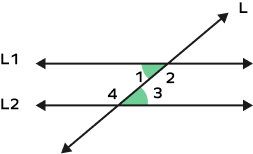
Solution:
As we can see from the figure, $\angle 1$ and $\angle 3$ are alternate interior angles, By the property of alternate interior angles, these angles will be equal.
Therefore, the measure of angle 3 will also be $105^\circ$.
$m \angle 3 = 105^\circ$.
5. In the figure given below, if $m\angle 1 = 100^\circ$, what will be the measure of:
i) $4$
ii) $\angle 3$
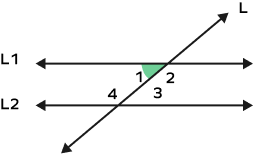
Solution:
i) As we can see from the figure, $\angle 1$ and $\angle 4$ are co-interior angles. The sum of co-interior angles is $180^\circ$.
Let the measure of the angle 4 be x.
Hence, we get the equation:
$100^\circ + x = 180^\circ$.
Therefore, x is equal to $80^\circ$.
ii) $\angle 1$ and $\angle 3$ are alternate interior angles. Thus, they are equal.
$m\angle1 = m\angle3 = 100^\circ$
Practice Problems on Interior Angles
Interior Angles - Definition, Theorem, Formula, Types, Examples
In an irregular pentagon, four of its angles are: $100^\circ,\; 90^\circ,\; 95^\circ$ and $105^\circ$. What is the measure of its fifth angle?
We know that the sum of angles of a pentagon is $540^\circ$.
Let the unknown angle be x.
$100^\circ + 90^\circ + 95^\circ + 105^\circ + x = 540^\circ$
$390^\circ + x = 540^\circ$
$x = 540^\circ\;-\;390^\circ$
$x = 150^\circ$
Therefore, the value of the unknown angle is $150^\circ$.
What is the sum of interior angles of a polygon with 12 sides?
We know that the formula to calculate the sum of interior angles of any polygon with “n” sides is
$Sum = (n\;−\;2)\times180^\circ$
Here, $n = 12$
$Sum = (12\;-\;2)\times180^\circ = 10\times180^\circ = 1800^\circ$
Therefore, the sum of interior angles of a polygon with 12 sides is $1800^\circ$.
In the above example, if the polygon is a regular polygon, what will be the measure of each angle?
If the 12 sided polygon is regular, then the measure of each angle will be the total sum of all angles divided by the number of sides.
So, $\frac{1800^\circ}{12} = 150^\circ$.
Hence, the measure of each angle in a 12 sided regular polygon is $150^\circ$.
In the figure given below, if the measure of angle 1 is $120^\circ$, what will be the measure of angle 3?
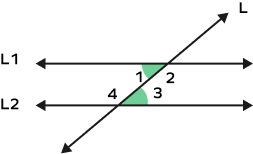
As we can see from the figure, $\angle1$ and $\angle3$ are alternate interior angles. By the property of alternate interior angles, these angles will be equal.
Therefore, $m\angle3 = 120^\circ$.
Identify the pair of co-interior angles.
$\angle2$ and $\angle3$ form a pair of co-interior angles. They lie on the same side of the transversal. Another pair of co-interior angles are: $\angle1$ and $\angle4$.
Frequently Asked Questions on Interior Angles
What are the types of triangles based on the measure of interior angles?
There are three types of angles based on the measure of interior angles.
- Acute Triangles: All the three internal angles of the triangle are acute
- Obtuse Triangles: Any one of the angles is an obtuse angle (greater than $90^\circ$).
- Right Triangles: One angle measures 90 degrees.
What are the parts of an angle?
Vertex: The corner point where the arms meet.
Arms: Two rays that meet to form an angle.
What are acute angles?
Angles that are between $0^\circ$ and $90^\circ$ are known as acute angles.
What are obtuse angles?
Angles that are greater than $90^\circ$ but less than $180^\circ$ are known as obtuse angles.
What are supplementary angles?
When the sum of two angles is $180^\circ$, each of the two angles are called supplementary angles.
What is the interior of an angle?
Interior of an angle definition in geometry: It is the region or area between the two rays that form the angle. It extends indefinitely from the vertex to infinity.





























