What Is a Reflex Angle?
The angles that lie between a straight angle $(180^{\circ})$ and a complete angle $(360^{\circ})$ are called reflex angles.
Consider a few examples.
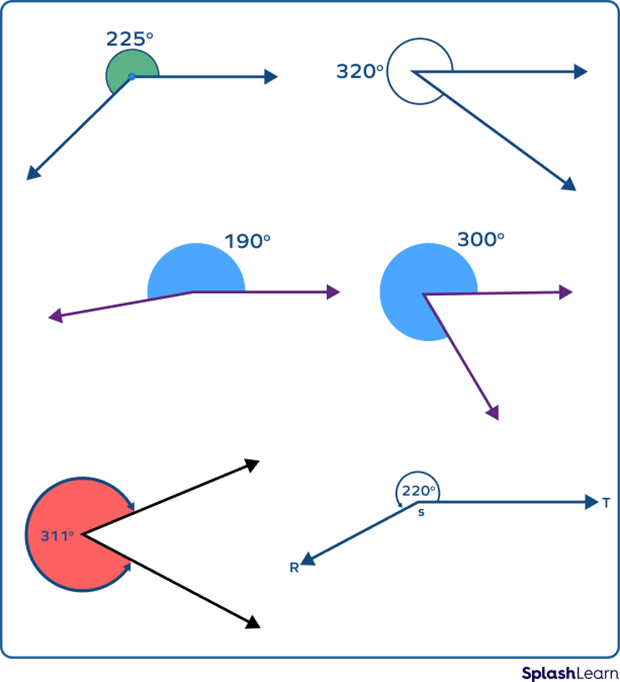
Here, you can see that any reflex angle has a corresponding angle (angle that lies on the other side of it). These two angles together form a complete angle of $360^{\circ}$. This corresponding angle may be an acute angle, obtuse angle, or even a right angle. So, for every acute angle, obtuse angle, and right angle, there is a reflex angle.
Recommended Games
Reflex Angle Definition
A reflex angle is defined as an angle that is greater than $180^{\circ}$ but less than $360^{\circ}$.
In other words, the definition of reflex angle in geometry can be given as an angle greater than $180^{\circ}$ (a half-circle ) and less than $360^{\circ}$(a full circle).
Recommended Worksheets
How to Find the Reflex Angle
We know that the sum of a reflex angle and its corresponding angle is 360 degrees.
Reflex angle $+$ Corresponding angle $= 360^{\circ}$
Using this relation, we can easily calculate the measure of the reflex angle.
Example 1: If an acute angle measures $65^{\circ}$, then its corresponding reflex angle will be
$360^{\circ} \;-\; 65^{\circ} = 295^{\circ}$.
Example 2: If an obtuse angle measures $100^{\circ}$, then its corresponding reflex angle degrees will be $360^{\circ}\;-\; 100^{\circ} = 260^{\circ}$.
Thus, if we know the measure of one acute or obtuse angle, the measure of the reflex angle can be calculated.
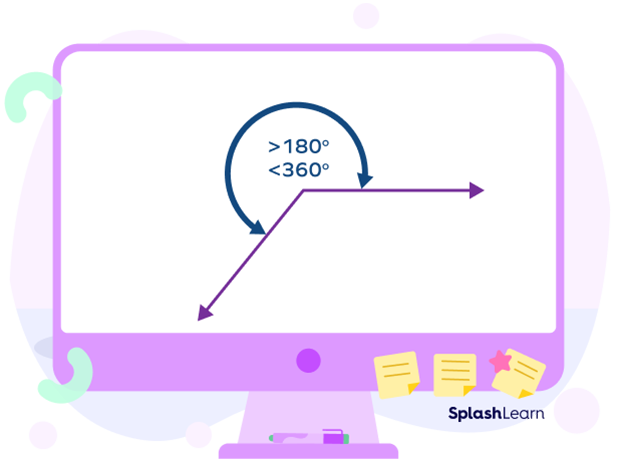
Reflex Angle Diagram
Reflex angle is more than $180^{\circ}$ and less than $360^{\circ}$.
Examples of reflex angle degrees: $181^{\circ},\; 190^{\circ},\; 200^{\circ},\; 210^{\circ},\; 220^{\circ},\; 230^{\circ},\; 240^{\circ},\; 250^{\circ},\; 260^{\circ},\; 270^{\circ},\; 280^{\circ},\; 290^{\circ},\; 300^{\circ},$
$310^{\circ},\; 320^{\circ},\; 330^{\circ},\; 340^{\circ},\; 350^{\circ},\; 359^{\circ}$, etc.
How to Measure a Reflex Angle
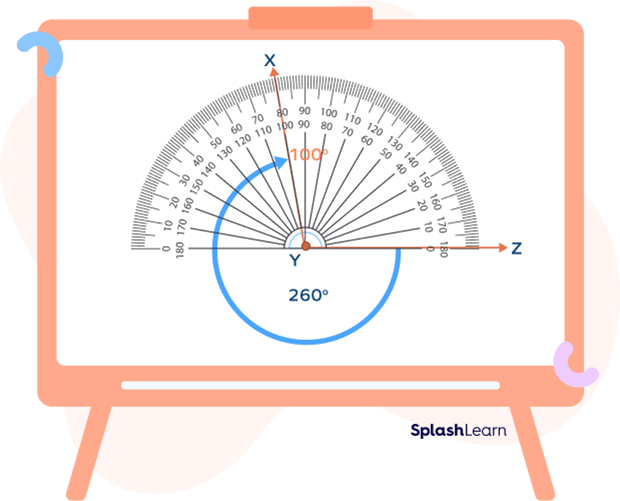
Reflex angle can be easily measured with the help of a protractor. We measure a reflex angle in two ways:
- Measure the corresponding angle and then subtract it from $360^{\circ}$.
Step 1: Measure the internal angle with the help of a protractor. Here, the measure of the internal angle is $100^{\circ}$.
Step 2: Subtract the value of this angle from $360^{\circ}$ to get the value of the reflex angle. This gives us $360^{\circ} \;-\; 100^{\circ} = 260^{\circ}$.
- Use a full-circle protractor to measure the reflex angle itself.
A full-circle protractor is a round protractor. It is very convenient when measuring an angle greater than 180 degrees. Place your protractor so that its base line lines up with one side of the angle. Identify the marking corresponding to the other arm of the angle. It represents the measure of the reflex angle.
Relation between Reflex Angle and Straight Angle
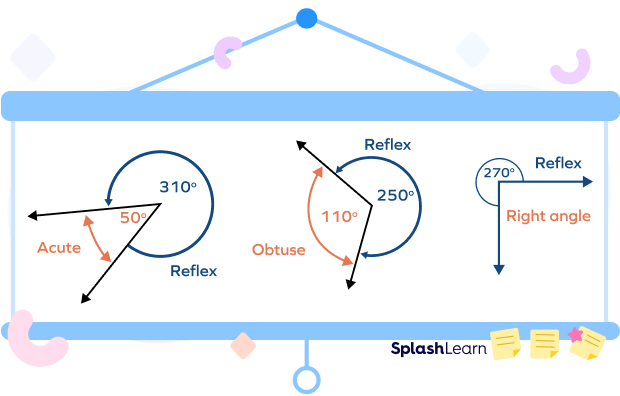
A reflex angle is equal to the sum of 180 (straight angle) and another angle, which may be acute, obtuse, or right angle.
For example, in the given image, we have
$210^{\circ} = 180^{\circ} + 30^{\circ}$ … the sum of $180^{\circ}$ and an acute angle
$290^{\circ} = 180^{\circ} + 110^{\circ}$ … the sum of $180^{\circ}$ and an obtuse angle
$270^{\circ} = 180^{\circ} + 90^{\circ}$ … the sum of $180^{\circ}$ and a right angle
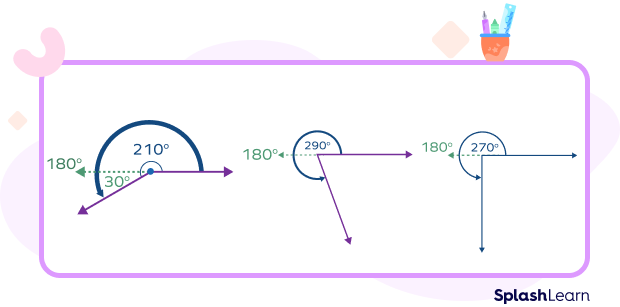
Thus, we can write these relations as
- Reflex angle $= 180^{\circ} +$ Acute angle
- Reflex angle $= 180^{\circ} +$ Obtuse angle
- Reflex angle $= 180^{\circ} +$ Right angle
Reflex Angle Around Us
Here are a few examples of objects in daily life showing a reflex angle.

Facts about Reflex Angle
- Reflex angles appear to be “turned back” or “reflected” beyond a straight angle.
- In radians, a reflex angle measures greater than radians and less than 2 radians.
- Angles around a point add up to 360 degrees.
Conclusion
In this article, we have learned about reflex angles. Understanding how these special types of angles function can help us better understand the concepts, such as measuring polygons and triangles as well as calculating areas accurately. Now let’s solve some examples and practice problems.
Solved Examples on Reflex Angle
1. What is the corresponding reflex angle of 160 degrees?
Solution:
We know that $160^{\circ} +$ reflex angle $= 360^{\circ}$
Reflex angle $= 360^{\circ} \;-\; 160^{\circ}$
$= 200^{\circ}$
Thus, the reflex angle of 160 degrees is $200^{\circ}$.
2. Identify reflex angles.
a) $140^{\circ}$
b) $30^{\circ}$
c) $300^{\circ}$
Solution:
a) $140^{\circ}$ is an obtuse angle as it is an angle between $90^{\circ}$ and $180^{\circ}$.
b) $30^{\circ}$ is an acute angle as it is an angle less than $90^{\circ}$.
c) $300^{\circ}$ is a reflex angle as it is more than $180^{\circ}$ but less than $360^{\circ}$.
3. What is the measure of angles made by the hands of a clock at 05:00?
Solution:

12 divisions $= 360^{\circ}$
1 division $= \frac{360}{12} = 30^{\circ}$
At 5 o’clock, the hour hand is at 5 and the minute hand is at 12.
Number of divisions covered $= 5$
The angle between the two hands of the clock at 5 o’clock $= 5 \times 30 = 150^{\circ}$, which is an obtuse angle.
The other angle is a reflex angle.
$360^{\circ} \;–\; 150^{\circ} = 210^{\circ}$
4. What is the reflex angle formed by an acute angle of $60^{\circ}$?
Solution:
Reflex angle $+$ Corresponding angle $= 360^{\circ}$
The reflex angle $= 360^{\circ}\;-\;$ acute angle
$= 360^{\circ} \;-\; 60^{\circ}$
$= 300^{\circ}$
Practice Problems on Reflex Angle
Reflex Angle - Definition, Diagram, Examples, Facts, How to Draw
Reflex angle is greater than _____ angle but less than _____angle.
Reflex angle is the angle which is greater than 180 degree (straight angle) and less than 360 degree (complete angle).
Which of the following are reflex angles?
Reflex angle is between $180^{\circ}$ and $360^{\circ}$.
Thus, $181^{\circ}$ is a reflex angle.
The measure of angle x is _______.
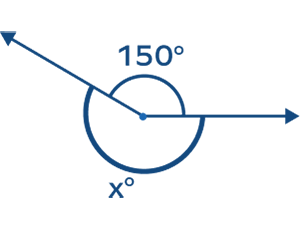
The measure of the complete angle is 360 degrees.
Thus, $x^{\circ} + 150^{\circ} = 360^{\circ}$.
$x^{\circ} = 360^{\circ} \;-\; 150^{\circ} = 210^{\circ}$
Which of the following is a reflex angle?
$250^{\circ}$ is a reflex angle because it lies between $180^{\circ}$ and $360^{\circ}$.
Find the corresponding reflex angle.

Reflex angle COD $=$ Complete angle - Measure of corresponding acute angle
$= 360^{\circ} \;-\; 36^{\circ}$
$= 324^{\circ}$
Frequently Asked Questions about Reflex Angle
What are the types of angles based on measurement or magnitude?
Types of angles based on the measurement are:
- Right angle: exactly $90^{\circ}$
- Straight angle: exactly $180^{\circ}$
- Reflex angle: between $180^{\circ}$ and $360^{\circ}$
- Obtuse angle: between $90^{\circ}$ and $180^{\circ}$
- Acute angle: less than $90^{\circ}$
- Complete angle: exactly $360^{\circ}$
What are the types of angles based on the rotation?
The angles are of two types based on the direction in which the initial arm rotates to form an angle.
- Positive Angles: An angle formed by counterclockwise rotation from its initial side is called a positive angle.
- Negative Angles: Negative angles are formed by clockwise rotation from the baseline.
What is the difference between obtuse and reflex angle?
An angle between $90^{\circ}$ and $180^{\circ}$ is obtuse. An angle greater than $180^{\circ}$ but less than $360^{\circ}$ is reflex.
Is there a reflex angle in triangles?
As the total sum of all angles in a triangle is $180^{\circ}$, it is not possible to have a reflex angle in a triangle.
What type of polygons can have a reflex angle?
A concave polygon has at least one reflex angle. Convex polygons cannot have a reflex angle.





























