What Is a Complete Angle in Math?
A complete angle is an angle that measures $360^{\circ}$. It represents a complete turn or full rotation and thus forms a circle around a point. A complete angle is also called a full angle, a round angle, or a perigon.
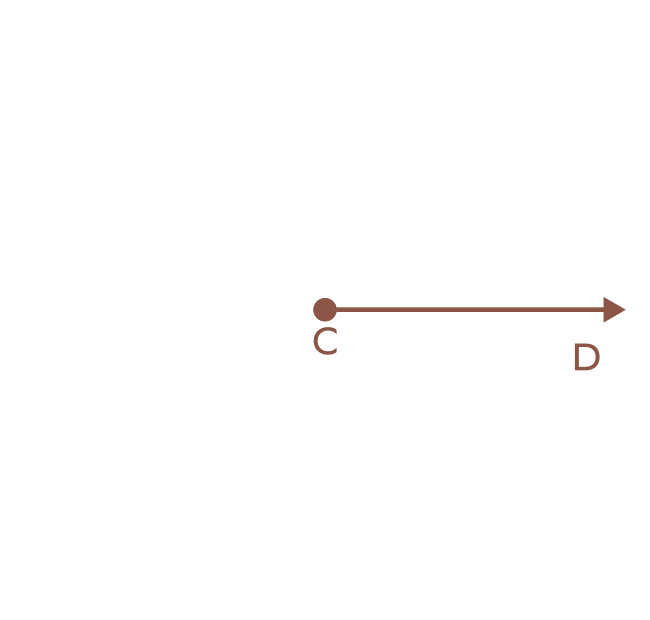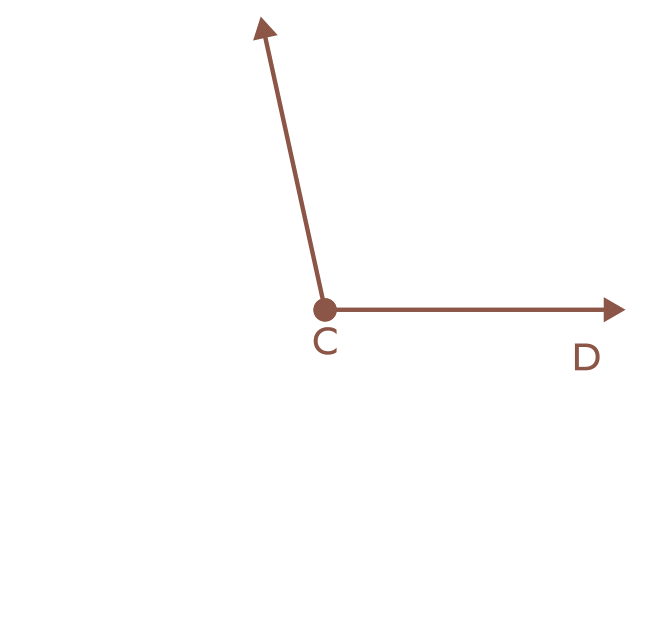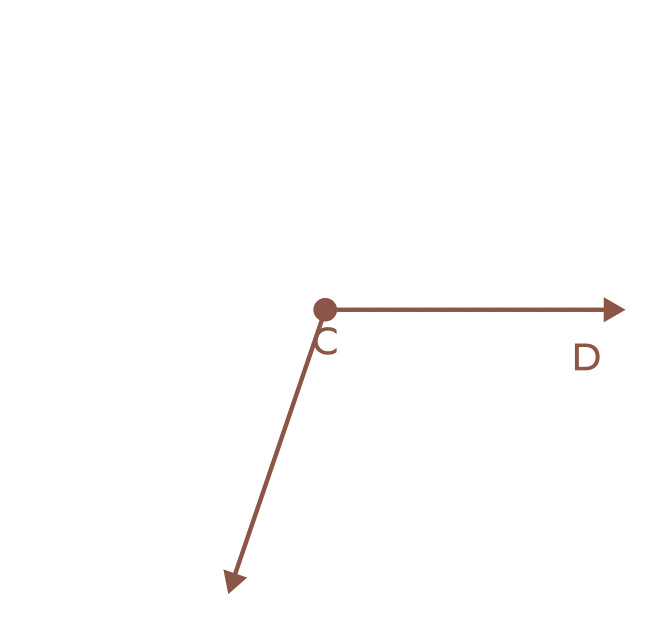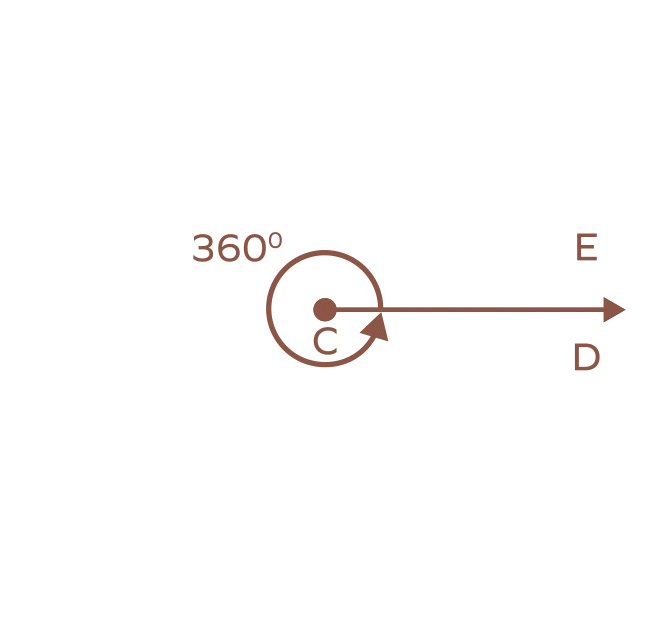
We know that if two rays meet at a common point (vertex), then an angle is formed. It is measured in units like “degrees” or “radians.”
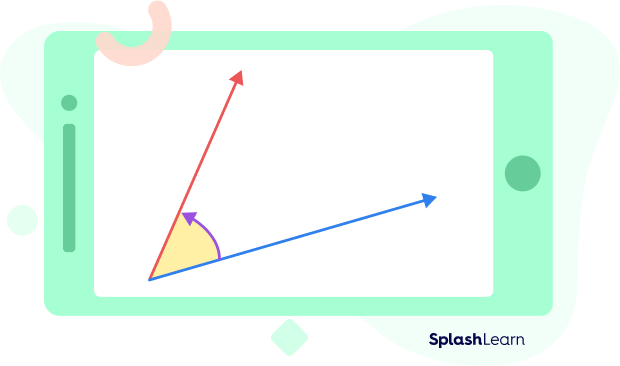
If the amount of turn around a point is equal to 360 degrees then the angle formed is a complete angle. Hence, a complete angle in math is a type of angle with a $360^{\circ}$ measurement.

Recommended Games
Definition of a Complete Angle
The complete angle is the angle formed when the incident or initial ray and the final ray coincide after a complete rotation or 360 degrees rotation.
One 360 degrees rotation is equivalent to $2\pi$ radians.

Recommended Worksheets
Formation of Complete Angle
A complete angle or a $360^{\circ}$ angle is formed when a ray completes a full rotation. It is the angle made by a ray to reach its final position from its initial position in a full rotation.
Let’s consider two rays, OA and OB.
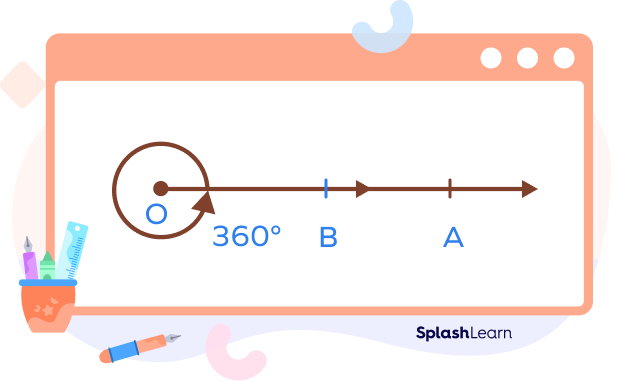
If OB takes a full turn and comes back to its original position, the angle between the two rays is the complete angle.
$\angle AOB = 360^{\circ}$
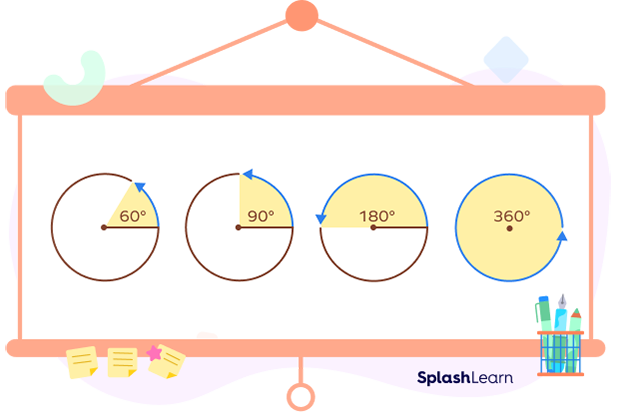
A complete angle is 6 times a $60^{\circ}$ angle, 4 times a right angle, and 2 times a straight angle.
Construction of Complete Angle
How can we draw a complete angle? We can easily construct a complete angle using a protractor or a compass.
Construction of a Complete Angle using a Protractor
The 360-degrees-protractor can be used to draw a complete angle easily. It is round in shape.

Construction of a Complete Angle Using Compass
To draw a complete angle using a compass, first draw a ray PQ. Put the pointer of the compass on the endpoint P and take a suitable width on the compass. Put the pencil tip on the ray PQ and draw a complete circle such that it meets the initial point in the end.

Complete Angles Around Us
Let’s take a look at a few examples of a complete angle in real life.

Facts about Complete Angles
- Wall clocks use the concept of full angles to show time.
- Four right angles or two straight angles make one complete angle.
- “Angulus” is the Latin word from which the word angle is derived. It means ‘corner.’
Conclusion
In this article, we learned about the complete angle, its real life applications, formation, and representation. Let’s now look at some solved examples and do some practice problems to understand the concept better.
Solved Examples on Complete Angle
- Check whether the pair of angles given below add up to a complete angle or not.
(i) $170^{\circ},\; 180^{\circ}$ (ii) $115^{\circ},\; 244^{\circ}$ (iii)$120^{\circ},\; 240^{\circ}$
Solution:
A complete angle is equal to $360^{\circ}$
(i) $170^{\circ},\; 180^{\circ}$
Sum of angles $= 170^{\circ} + 180^{\circ} = 350^{\circ} \neq 360^{\circ}$
Therefore, the pair $(170^{\circ},\; 180^{\circ})$ does not make a complete angle.
(ii) $115^{\circ},\; 244^{\circ}$
Sum of angles $= 115^{\circ} + 244^{\circ} = 359^{\circ} \neq 360$
Therefore, the pair $(115^{\circ},\; 244^{\circ})$ does not make a complete angle.
(iii) $120^{\circ},\; 240^{\circ}$
Sum of angles $= 120^{\circ} + 240^{\circ} = 360^{\circ}$
Therefore, the pair $(120^{\circ},\; 240^{\circ})$ makes a complete angle when added.
- Jane runs around a circular park in the morning from point A to point A. What kind of angle does her path make at the center? What does the distance covered by her in 1 round around the circular park represent?
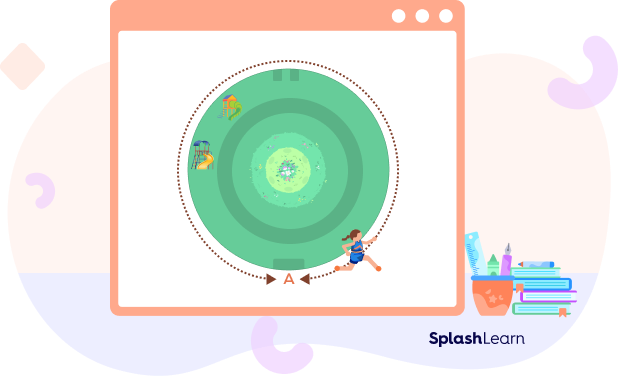
Solution:
Jane completes an entire round around a circular park from point A and ending at the same point. So, her path makes a full circle.
The angle made around the center of a circle is 360 degrees.
Thus, Jane’s path represents a complete angle at the center.
Also, the distance covered by her in 1 round represents the circumference of the circle.
- In the figure given below, find the relation between the angles “a” and “b.”

Solution:
As we know, the sum of angles around a point $=$ Complete angle $= 360^{\circ}$
So, $135^{\circ} + 65^{\circ} + a + b = 360^{\circ}$
$200^{\circ} + a + b = 360^{\circ}$
$a + b = 360^{\circ} \;–\; 200^{\circ}$
$a + b = 160^{\circ}
Hence, the relation between “a” and “b” is $a + b = 160^{\circ}$.
- In the figure given below, calculate the value of “x.”
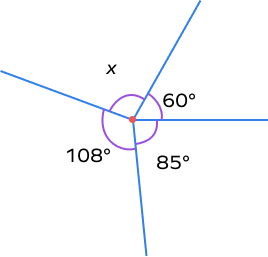
Solution:
As we know, the sum of angles around a point $= 360^{\circ}$
So, $108^{\circ} + 85^{\circ} + 60^{\circ} + x = 360^{\circ}$
$253^{\circ} + x = 360^{\circ}$
$y = 360^{\circ} \;–\; 253^{\circ} = 107^{\circ}$
Hence, the value of x is $107^{\circ}$.
- If three angles made at the center of a circle are $145^{\circ},\; 90^{\circ}$, and y. Find the value of y.
Solution:
Given angles made at the center of a circle: $145^{\circ},\; 90^{\circ}$, and y.
As we know, the sum of angles at a point $= 360^{\circ}$
So, $145^{\circ} + 90^{\circ} + y = 360^{\circ}$
$235^{\circ} + y = 360^{\circ}$
$y = 360^{\circ} \;–\; 235^{\circ} = 125^{\circ}$
Hence, the value of x is $150^{\circ}$.
Practice Problems on Complete Angle
Complete Angle: Definition, Formation, Examples, Facts, FAQs
The sum of all angles around a point equals _____.
The sum of all angles around a point equals $360^{\circ}$.
What is the ratio of a right angle to a complete angle?
The ratio of a right angle to a complete angle $= 90^{\circ} : 360^{\circ} = 1: 4$
A full rotation angle can be divided into how many straight angles?
A straight angle measures $180^{\circ}$. So, two straight angles add up to $360^{\circ}$. Hence A full rotation angle can be divided into two straight angles.
In which system is a complete angle represented as $360^{\circ}$?
In the sexagesimal system, a complete angle is represented as $360^{\circ}$.
In radians, a complete angle is represented as _____.
In radians, a complete angle is represented as $2\pi$.
Frequently Asked Questions about Complete Angles
What are the types of angles?
The six major types of angles, based on measurement, are right angle, straight angle, reflex angle, obtuse angle, acute angle, and complete or full rotation angle.
How is the complete angle different from a reflex angle?
A complete angle is an angle that measures 360 degrees. A reflex angle, on the other hand, is an angle that is greater than 180 degrees but less than 360 degrees.
What is the application of angles in math?
Engineers and architects use angles for measurement, designing roads, building, etc. Carpenters use it to make equipment like chairs, sofas, tables, etc. Artists use their measurement knowledge to sketch or create art pieces.
How are complete angles measured?
Degrees or radians are typically used to measure angles. Any unknown angle can be measured with a protractor or a measuring tool.
Is $180^{\circ}$ angle a complete angle?
No, a $180^{\circ}$ angle is a straight angle. A $360^{\circ}$ angle makes a complete angle.
What is a 360 degree angle called?
A 360 degree angle is called a complete angle.




































